自我建构，让概念的本质更明晰

余夕凯

[摘 要]“认识分数”是苏教版教材三年级上册的内容，是学生第一次接触分数。著名特级教师周卫东一次有力的尝试，解答了教师最常关注的问题：学生对分数有认识吗？学生心中的分数能用文字或图形进行表征吗？如何基于学生已有的经验展开这节课的教学？如何让具有差异的学生都能深刻理解分数？

[关键词]概念本质;自我建构;认识分数

臺湾学者黄武雄在《学校在窗外》中提到：孩子到学校是为了与世界互动，打开经验与世界的联结;教学的一个任务是调动学生已有的经验，并进行抽象与创造能力，以便于与世界的联结。“认识分数”这节课我不知道听过多少次，每每看到这个课题，头脑中都能勾勒出一个基本的教学框架：这节课需要达成的几个目标，学生在学习这部分内容时可能遇到的困难，以及思想层面和思维层面应该给予的关注。当听说周卫东老师要重新演绎这一经典案例时，我在佩服的同时不免有些担心——他能实现什么样的突破？

【教学赏析】

师（课件呈现猪八戒）：今天我给大家带来了一个新朋友。

（我心里咯噔一下，这个猪八戒伴随着“认识分数”已经走过了一年又一年，为什么还要选取这个经典的“老人”？但后面的环节告诉我，虽然对于我来说猪八戒是一个“老人”，但对于三年级的学生来说，在认识分数这个情境中，猪八戒还是新人，这个角色还是有他独特的魅力，也有着不可替代的作用。）

师：猪八戒肚子饿了，先向农民伯伯要了两块饼。（出示两块饼的图）但是猪八戒还是没吃饱，接下来会要几块？（出示一块饼的图）

生1：一块。

师：猪八戒吃完一块后，还是没吃饱，接下来会要几块？

生2：半块。

师：还有没有别的？

生3：二分之一块。

生4：三分之一块。

生5：四分之二块。

【赏析：学生根据两块、一块，自然联想到半块，但是周老师并没有揭示结论，而是继续追问。这样的追问，启发了学生的思维，勾连了数与形之间的关系。这样的问题也让周老师对学生的认知情况有了很好的了解：从学生的回答中能够感受到他们对分数有一定的认识，部分学生甚至知道可以用[12]表示半块饼。】

师：猪八戒没学过数学，他说我只要一小块。你们想一想，一小块到底有多大？老师给你们每人一张纸，请想象这一小块在你心目中可能的形象，开始撕吧！

【赏析：课堂教学要留白，留更多的时间与空间，让学生去创造、去想象、去尝试、去表达。这样的一小块是什么样的？它与整体是什么样的关系？学生在头脑中需要建构图形，并要用内心的想法去支撑自己的行为，这一“撕”真好！】

师：为什么三位小朋友撕出来的大小不一样？

生6：他们理解的一小块都是不一样的。

师：理解不一样，撕出来的就不一样。

生7：猪八戒没有说清楚是多大的一小块。

师：猪八戒没有说清楚，是因为他不懂数学啊。

【赏析：教师提出的问题，逼着学生向概念的本质迈进。学生在回答问题的时候，要站在别人的视角去思考，首先要在头脑中建构图形，然后才有动作行为。这样的想象能够发展学生的空间观念，使学生学会质疑、学会判断，这样的数学学习很重要。】

师：猪八戒要的饼就是图中的涂色部分。它到底有多大？请你用一句话或一个数来表述。

生8：半块。

生9：不对，应该是半块中的半块。

生10：四份中的一份。

生11：应该是四等份中的一份。

生12：分成四份，取出其中的一份。

生13：应该是平均分成四份，取出其中的一份。

【赏析：从以上学生的回答中能感受到部分学生的认知是不完整的、不严谨的。因为每一个学生思考得都比较充分，不同层次的学生就能在相互倾听、补充、质疑、批判中修正了对分数本质的理解。可见，好的学习任务能调动学生已有的认知经验，激发学生的思维，使学生不但完善了认知，还学会了学习。】

师（出示一个学生的作品“[41]”）：我请这个作品的主人说说为什么这么写。虽然他的写法和大伙不一样，但是他的发言中一定会有合理的成分，如果他讲得对，我们给他掌声。

师：4是什么意思？

生14：是把这个饼分成4份。（有学生补充：是平均分成4份）

师：1是什么意思？

生14：四份中的一份。

师：尽管他这个四分之一跟你们写得不一样，但是他有没有说清楚4和1的道理？

生（齐）：有。

师：这就叫作学习，明白了吗？

（在充分讨论的基础上，师生共同总结：[14]就是把一块饼平均分成4份，其中的一份是它的四分之一）

【赏析：周老师让学生用自己的方式去表达，学生想到利用图形、文字、数字，虽然有正确的，也有错误的，但多元的表征方式，能够促进学生深刻理解。这里，周老师不疾不徐，让学生充分讨论、交流，既有对正确方法的肯定，也有对错误方法的价值挖掘。学生出现这样的错误肯定是在教师的预设之中的，关键是如何有效利用这个资源，发挥错误的价值。周老师抓住问题的本质，先抛开形式的错误，深入挖掘概念的内涵，强化了所有学生的认知，同时也很好地保护了出错的学生。】

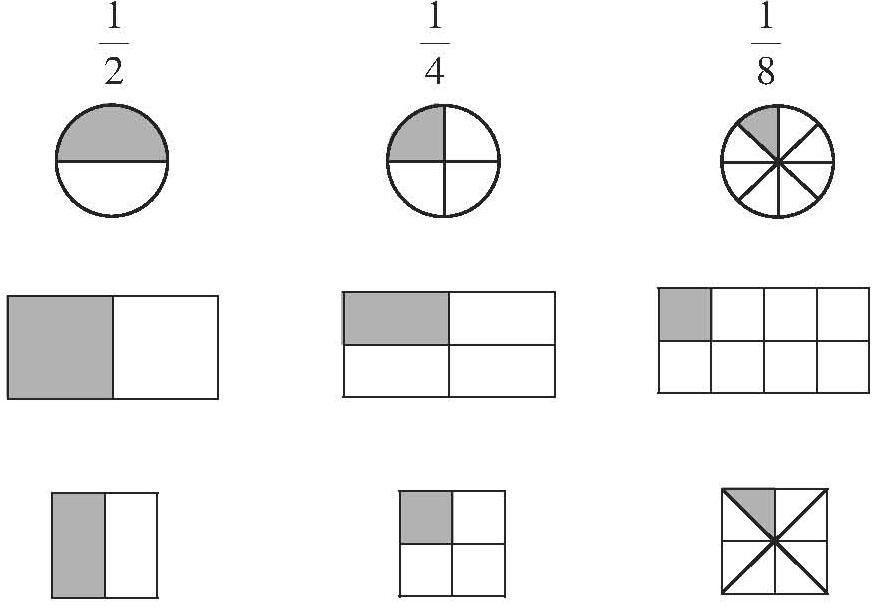
师（在黑板上呈现 [12]、[14]、 [18]）：请选择其中一个进行研究。怎么研究？你可以折一折、分一分，再涂一涂、说一说。

师：观察最后一排，都是同样大小的正方形，为什么一个表示二分之一，一个表示四分之一，而另一个却表示八分之一？

生15：因为对折的次数不一样，得到的格子不一样，所以涂色部分就不一样了。

生16：因为平均分的份数不一样，所以分数就不一样。

师：竖着看最后一列，图形不一样，为什么都可以用八分之一来表示？

生17：因为它们对折的次数是一样的，都是三次。

师：对折三次意味着什么？把这个图形怎么样了？

生18：把这个图形平均分成了八份。

【赏析：周老师提供的素材和预设的问题都具有针对性。不管是什么样的图形，只要平均分的份数相同，都可以用几分之一来表示：同样大小的形状，只要平均分的份数不一样，得到的几分之一也就不一样。如何让学生理解分数本质，而抛弃非本质属性？通过动手操作来感受体验，通过问题展开思考抽象，这样的操作和交流非常有意義。】

师：猴哥说他把一块饼的[12]给师傅，再把剩下的[12]给沙僧。

师：猪八戒认为猴哥把一块饼分光了，是这样吗？

生19：没有分光。

生20：他第二次是分了剩下的一半，还没有分完。

师：没有分完，可能会是什么样的？仔细琢磨一下，两个[12]一样吗？

生21：不一样。第一个[12]是整个饼的，第二个[12]是剩下的，是一半的一半。

（教师根据学生的回答在课件上进行分割操作）

【赏析：通过分析比较两个[12]，让学生明晰“分的物品不一样，[12]表示的大小也不一样”。学生第一次接触“两个[12]表示的大小不一样”，理解起来还是比较困难的。周老师创设情境，借助直观图形，帮助学生突破了认知难点。这里能够看出周老师的别具匠心。在第一次教学分数时，教师通常都会回避单位“1”的不同情况，怕引起学生认知的混乱，但这节课上，由于周老师对教材的深度理解以及超强的课堂驾驭能力，学生的认知不但没有混乱，反而更加清晰和深刻。】

师：唐僧和沙僧都认为悟空最辛苦，他俩的饼还是给了悟空，那悟空能吃多少饼？

生22：能吃四分之三。

师：怎么解释这个四分之三？

生23：平均分了四份，吃了三份。

师：新的分数，除了几分之一，还可能有几分之几。

【赏析：这里的教学有余音绕梁的感觉。一般来说，教学完几分之一之后，这节课也就结束了。很显然，周老师要让学生感受到知识之间是相互关联的，他非常智慧地利用原有的情境，改变了问题，自然地引发学生思考，把学生的思维引向更深处。课虽然结束了，但是对分数的学习才开始，留给学生这样的一个可以延展的空间，是教师所应做到的。】

（责编 金 铃）