埋头弹药膛内压力波传播模拟研究

张文星，陆 欣

(南京理工大学 能源与动力工程学院， 南京 210094)

现代战争中，随着现代科技在战斗中的应用，对目标的击打能力要求越来越高，对火炮的战斗力要求也越来越高，而增强火炮火力的基本途径之一就是增大火炮口径[1]。但增大火炮口径会使整个火炮武器系统尺寸增大，这对于火炮的炮塔空间是无法接受的，所以埋头弹火炮系统的理念应运而生[2-7]。埋头弹火炮的理念最早是由美国空军实验室提出，并在其研究过程中投入大量经费，之后，英国和法国成立了一个国际联合公司研发埋头弹火炮。埋头弹是一种新型的弹药，这种弹药的结构特点是将弹丸埋在药筒内，弹体呈圆柱形；药筒的形状简单整齐，可以使供弹机设计简化；节省弹药储存空间，增加弹药携带量；由于弹药长度缩短，使得送弹距离短，射速快[8]。埋头弹火炮不同于以往的火炮，有着特殊的结构并且采用二次点火、程序燃烧。即先击发底火，火焰通过传火管点燃弹丸尾部的速燃药，速燃药点燃后一边推动弹丸沿导向管移动，一边逐渐点燃主装药，生成的燃气和火药颗粒接着沿导向管移动。

对于早期的火炮，膛压和初速度较低，装填密度较小，膛内的压力波动现象不明显，对内弹道性能的影响不大，所以在当时的内弹道设计中经常被忽略[9-10]。随着火炮武器系统的不断发展，对火炮内弹道性能有了更高的要求，火炮的装填密度、膛压、初速度得到了提高，这也导致了火炮膛内大幅值压力波的产生[11]。强压力波的存在不仅影响内弹道的性能，也影响弹丸、火炮以及整个武器系统的性能[12]。Cheng Cheng等人建立了两段流动模型用来模拟双流体流动的复杂物理过程，该模型提高了在内弹道循环期间描述气固两相流动规律的能力，并预测燃烧细节，如火焰蔓延，压力波的形成等[13]。Huahua Xiao等人进行数值模拟，研究了压力波对管内传播火焰的演变和稳定性的影响[14]。在之前的研究中，并未考虑埋头弹火炮发射过程中膛内的压力波变化，本文针对中口径埋头弹火炮，通过其内弹道两相流动模型数值模拟，分析压力现象。

1 埋头弹内弹道模型

1.1 基本假设

埋头弹火炮发射过程中膛内在轴向和径向有着两维的特点，膛内的物理量随时间和空间剧烈变化。关于膛内的压力波，并非是是稳定的周期震荡，而是沿轴向呈现不规则的分布，不是简单的二次曲线。所以在建立一维两相流模型时，做出如下假设：

1) 不考虑火药颗粒的压缩变形。

2) 假定火药固体颗粒是具有连续介质性质的一种拟流体，可以当做流体处理。

3) 弹丸在导向管中的运动不考虑摩擦力。

4) 主装药和速燃药燃烧产物相同，且火药燃气热力学参数为常数，火药燃烧生成物组分不变。

5) 膛内的速度、密度、空隙率、压力等两相流物理量均随着轴向位移和时间变化。

1.2 内弹道一维两相流模型

埋头弹火炮发射过程有着高压、高温和高速度的特点，在瞬间的化学反应中包含着火药燃烧、燃气膨胀和弹丸运动等[15]。由于其膛内发射过程极其复杂，故做了简化处理，建立一维两相流模型模拟膛内发射过程。

其控制方程为：

1) 气相连续方程

(1)

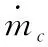
2) 气相动量方程

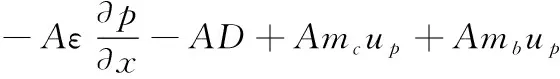
(2)

式中，p为气相压力，D为单位体积内相间阻力，up为固相速度。

3) 气相能量方程

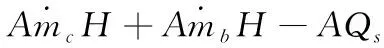
(3)

式中，e为气相比内能，H为火药燃烧焓，Qs为单位表面积相间热交换。

4) 固相连续方程

(4)

式中，ρp为固相密度，up为固相速度。

5) 固相动量方程

(5)

式中，τp为颗粒间应力。

2 压力波形成原因与特性

对于埋头弹膛内压力波传播特性的分析，主要是分析其膛内压力波分布，膛内压力波可以定义为火炮射击过程中膛内压力在纵向传递的波动现象。在工程上，一般计算出膛底压力与坡膛处所测压力的差值，通过压力差在时间上的变化表示压力波的变化。借助于内弹道一维两相流模型计算得到压力在时间以及空间上的分布，进而求得压力波曲线。

当击发底火后，产生的燃气引燃火药。火药颗粒表面温度被加热到着火点后，点火药附近的火药颗粒开始燃烧，导致膛底附近压力值高，出现了第一个正波值。当火药燃气和火药颗粒形成气、固两相后，压力梯度增大，会推动和挤压火药床朝着弹底部位运动，火药床被压缩时会传递压力波，使得火药颗粒会密集的聚集在弹底，火焰传过来后大量产生燃气，形成的压力梯度为反方向，这时出现了第一个负波值。由于反向压力梯度，火药床又聚集在膛底附近，产生第二个正波值，这样在膛底和弹底之间反复运动，就形成了膛内纵向压力波。

在膛内，随着弹丸运动，火药颗粒和火药燃气都会对压力波产生影响，所以膛内压力波受到气固两相共同的作用。当火炮引发底火后，膛内压力波现象具体表现为压力在时间曲线上的分布有着不光滑的“阶跃”现象，产生压力波现象主要是由波的反射、火药床移动和不均匀点火造成的。

3 计算结果及分析

对上述内弹道一维两相流模型，使用MacCormack方法求解控制方程，该方法是一种非中心显示有限差分格式，具有二阶精度。根据其初始条件、边界条件以及一些已知参数，得到与压力波有关的气固两相物理量在时间和空间上的分布，如图1～图6。

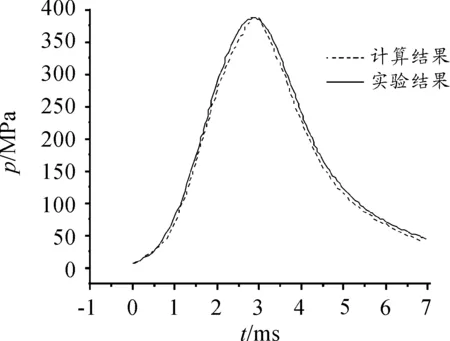
图1 坡膛压力实验结果和模拟计算结果

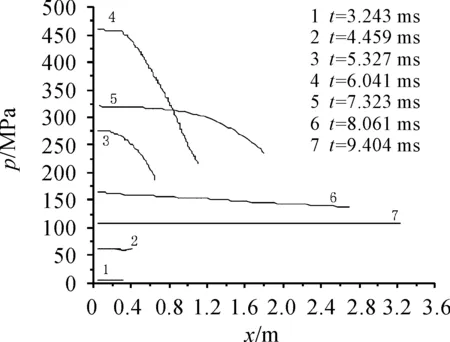
图2 压力分布图

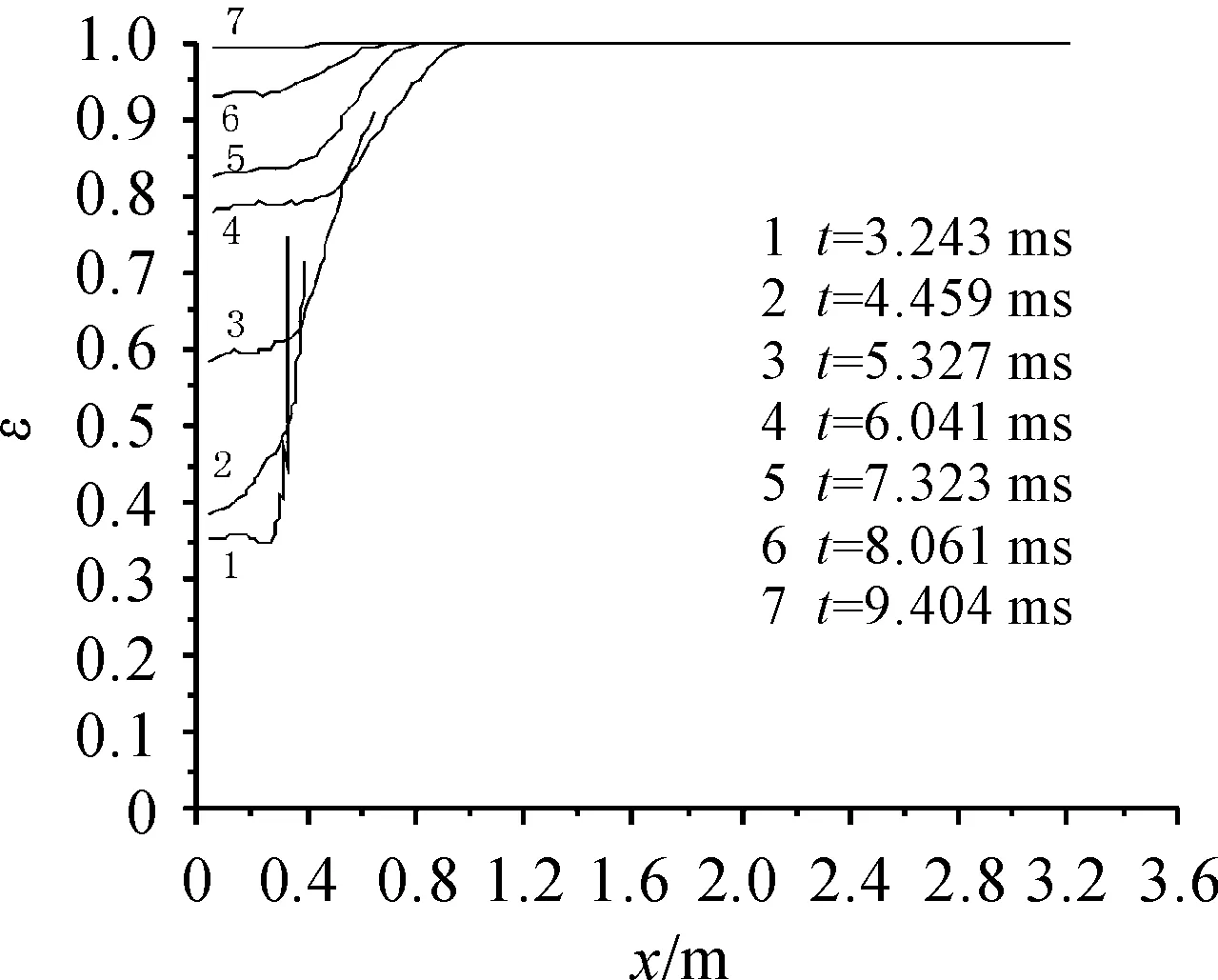
图3 空隙率分布图

图1所示为埋头弹坡膛处压力的实验所测结果和模拟计算结果，由图1可知计算结果和实验结果相符合，压力对比的结果说明采用的该埋头弹内弹道模型能够正确模拟，并且得到气固两相物理参数，可以使用该模型模拟埋头弹膛内压力波传播特性。

由图2可知，击发底火后，压力分布大致呈现为膛底高弹底低。造成这一现象的原因主要是由于主装药的分布主要集中在膛底，固相占比较大，在火药被点燃时会释放更多气体。

由图3可知，空隙率的分布呈现为膛底低弹底高，空隙率是表示气相体积占总体积大小的百分比。这是由于当速燃药被点燃时，会推动弹丸在导向管内移动，同时会先点燃弹丸底部的部分主装药，然后才会逐渐点燃膛底的主装药。

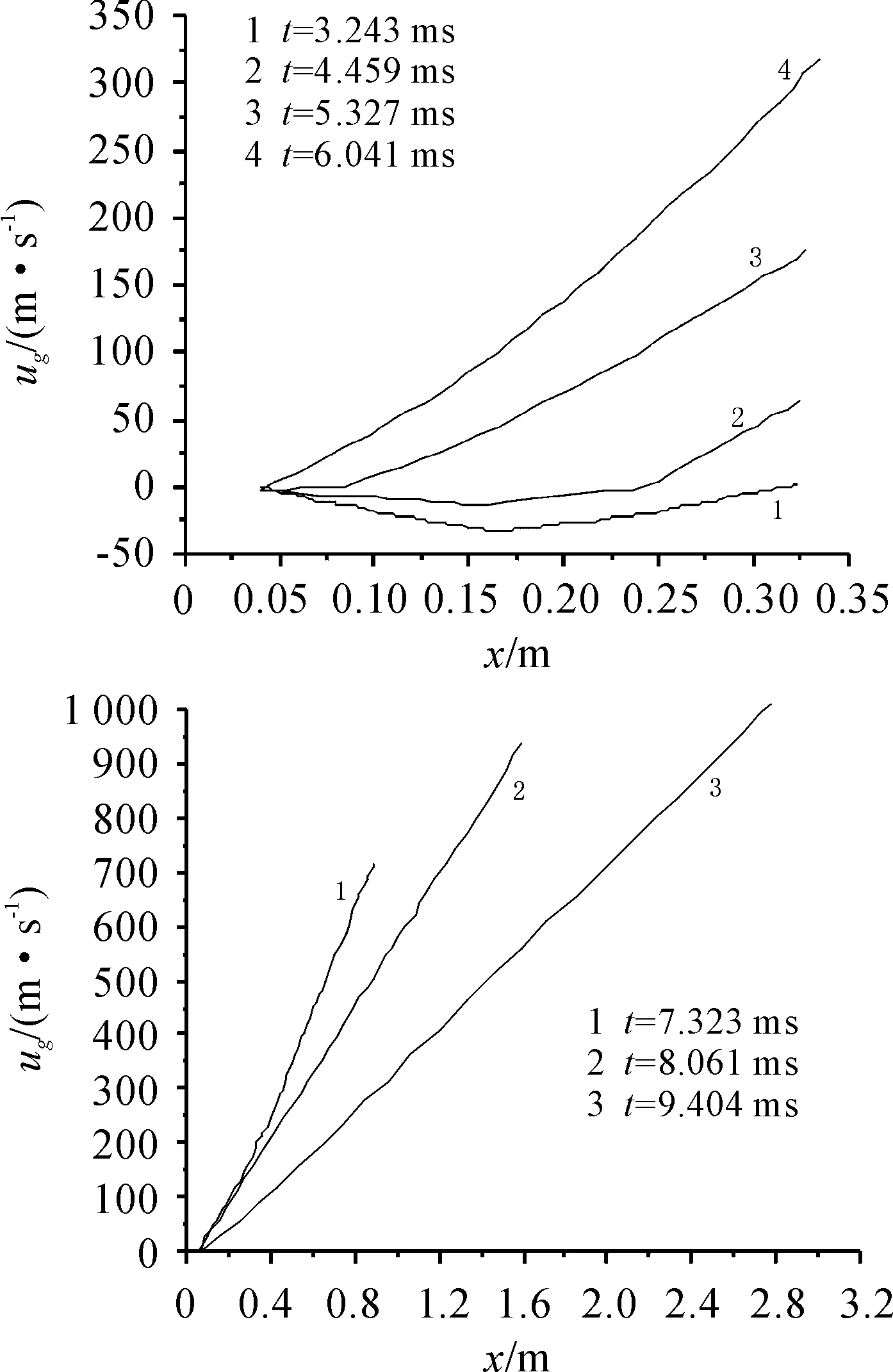
图4 气相速度分布图

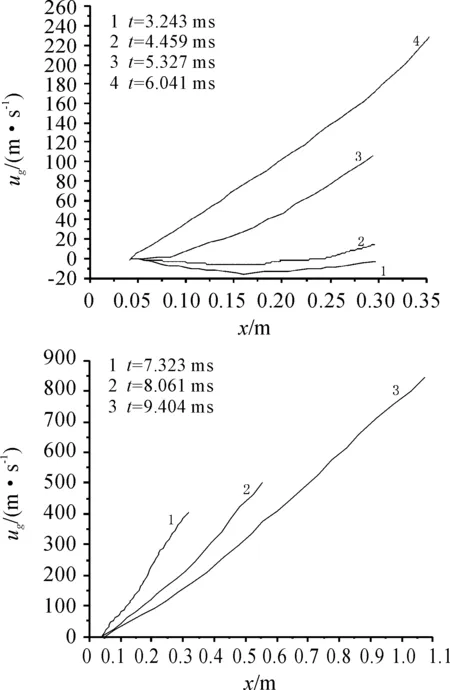
图5 固相速度分布图

由图4、图5可知在起始阶段，气相和固相速度有一段表现为负值，这是由于当速燃药被点燃后，会沿着药室反方向从弹底向膛底的顺序点燃主装药，此时火药燃气在推动弹丸运动的同时会推动主装药颗粒向后运动。之后随着弹丸运动，主装药被全部点燃，气相和固相速度迅速上升，且弹丸运动速度可看做弹底附近气相速度。

由图6可知：

1) 该装药条件压力波曲线具有波动性具有收敛性。当火药被点燃后压力波快速达到最大值并且迅速下降。第一个波峰最大，约为9.3 MPa，第一个波谷最小，约为-10 MPa，此后，振幅开始衰减，慢慢衰减为零。压力波分布不是稳定的周期振动，而是瞬变的非周期阻尼运动。

2) 压力波存在于点火后的初始阶段，最初由于局部点火，膛底颗粒密度高，空隙率低，形成第一个正波值，之后随着火药床的移动以及压缩，在弹底形成一个高密度区，当火焰传播到弹底使得弹底部位燃气快速产生形成了第一个负波值。

3) 之后火药床又被推动到膛底(表现为图4所显示的气相速度图和图5所表示的固相速度图中)，使得膛底火药颗粒密度高，燃气在膛底快速生成。振动周期和振动幅度随时间不断减小，最后为零。

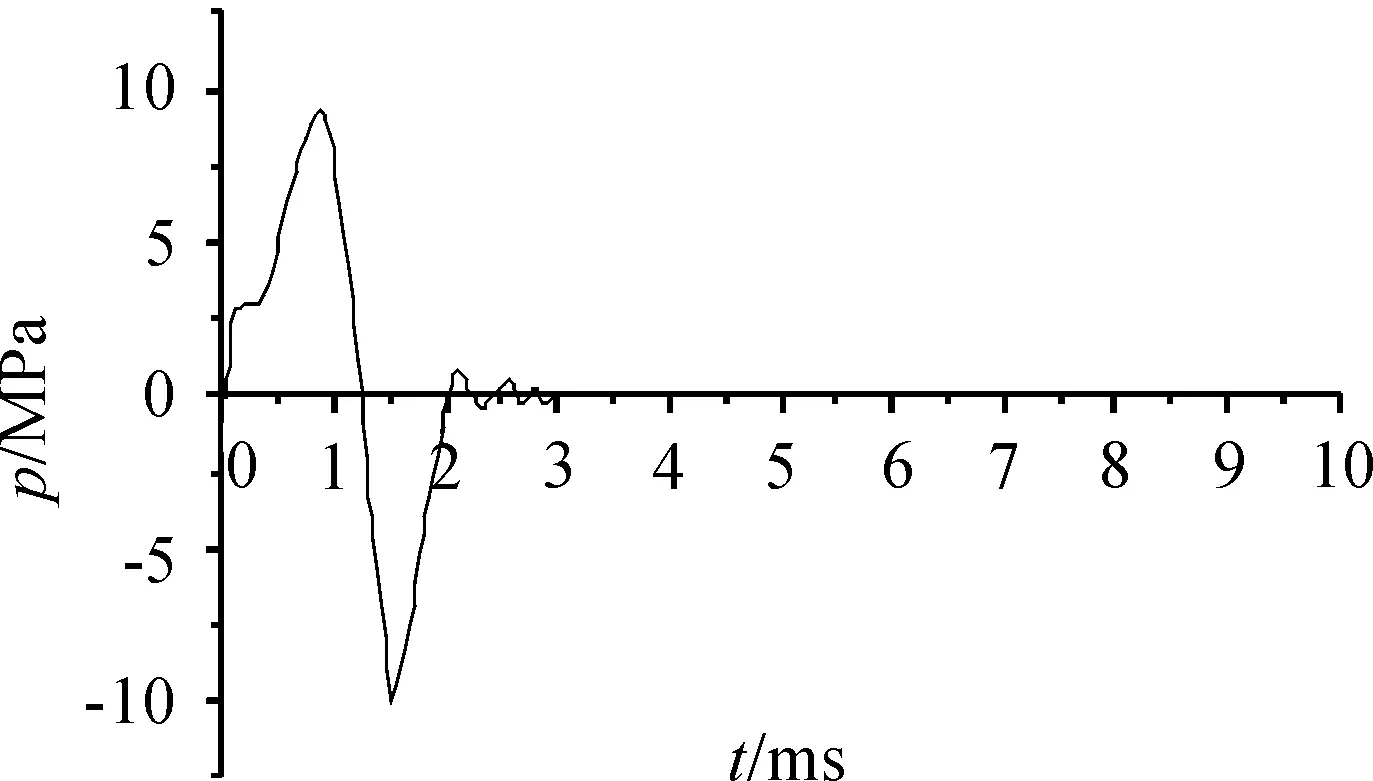
图6 压力波曲线

4 结论

击发底火后火药床在压力梯度作用下会在膛底与弹底之间运动，在该装药条件下，膛内压力波型具有收敛性，第一个正波值最大，约为9.3 MPa，第一个负波值最小，约为-10 MPa，出现一个正波值和一个负波值后，振幅逐渐衰减，在2 ms后压力波逐渐趋于零。