基于质量调谐技术的自旋弹丸姿态控制

杨 星,王 唯

(南京理工大学 瞬态物理国家重点实验室， 南京 210094)

现阶段有很多方法可以实现弹道控制，例如利用增阻减速型阻力执行机构结合自适应落点控制算法实现对弹丸射程的一维调控[1]、使用动力增程机构改变弹丸速度及运动方向[2]、以及通过舵翼附加气动力矩改变姿态角进而引起弹丸气动攻角和气动力的变化[3-4]等。在理论上，采用气动舵的控制精度较高，且可以实现连续调控；同时随着技术水平和工艺的提高，舵机体积日益减小，因此采用舵机的有控弹丸的有效载荷相对较大。尽管上述方法存在诸多优点，仍旧有一些缺陷不可避免，例如增加舵翼作为独立控制面时，受限于弹丸细长的外形，会在提供必要控制力(矩)的同时增加气动阻力，使原有弹丸的有效射程大幅减小。因此，如何能在不改变气动外形的前提下控制弹丸姿态运动进而实现弹道控制是现阶段的研究热点。

质量调谐技术[5]是一种利用附加的质量子系统平衡主系统受到的外力，用来减小主系统的受迫振动响应的方法。现阶段国内外都致力于将智能材料引入传统的质量调谐技术中[6]，例如电涡流质量调谐阻尼器[7]、混合动力调谐质量阻尼器(HATMD)[8]、杠杆式刚度可控阻尼器[9]等的出现，以及对传统质量调谐结构的改造[10-11]，都预示着子系统中的阻尼器和弹性元件将不再局限于常规的弹簧和阻尼器。随着相关技术的不断发展，质量子系统性能的按需即时调节已经成为可能。在航海领域，如何应用主动控制技术实现振动控制是当下的研究重点[12-14]。尽管质量调谐技术调控精准、效果显著，但在航空、航天等领域应用较少。

弹丸的姿态运动本质上可以简化为陀螺的角运动，其主轴在空间中的方位可根据文献[15]中提到的复球面理论映射到单位复球面上的点进行描述。如果弹丸内部存在一个类似陀螺的质量子系统与弹丸质心固联重合，就相当于在复平面上增加一个具有等效质量的等效“质点”。将这个质量子系统与弹丸通过恰当的约束进行联系，复平面内的双“质点”系统在等效作用力的运动与通常意义上的质量调谐系统具有相似的特性。

本研究参考质量调谐技术的基本原理，提出了一种基于双陀螺模型的姿态控制方法。基于选取的坐标系统，推导添加质量子系统的弹丸姿态运动模型。然后应用H∞控制方法推导姿态控制方程，以某型自旋稳定弹为例进行数值仿真，初步验证了本文提出方法的可行性与有效性。

1 原理分析与动力学模型

1.1 坐标系统的选取

相关平动与转动坐标系统的定义如下：

惯性坐标系Sg：本文使用的惯性坐标系与发射坐标系[16]的定义相同，其中坐标原点位于弹丸质心，xg轴在水平面内与初始射击方向相同；yg轴竖直向上；zg轴在水平面内，且由xg和yg的叉乘确定。

弹体坐标系St：弹体坐标系与弹丸固联，符合飞行力学的惯常定义[17]，坐标原点位于质心，各个坐标轴与惯性主轴重合，xt轴平行于弹体纵轴指向前；yt轴在弹体对称平面内，垂直于xt轴向上；zt垂直于弹体的对称平面，指向右。

为了区分弹丸与质量子系统，本文用x1t表示弹丸的弹体坐标系的横轴，x2t表示质量子系统的本体坐标系的横轴。

1.2 动力学模型

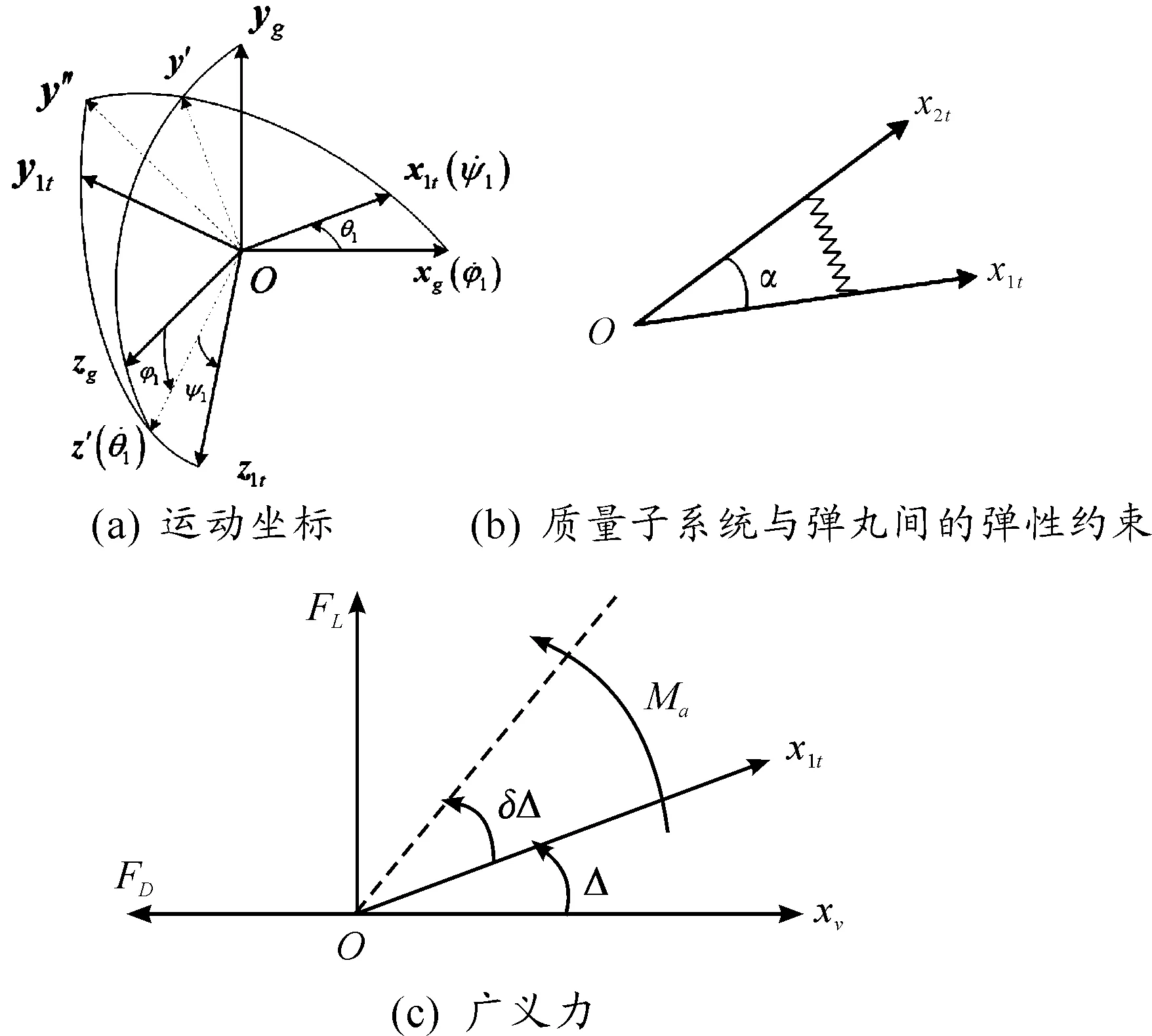
图1 弹丸姿态运动坐标及广义坐标定义

图1中，α表示弹丸主轴与质量子系统主轴间的夹角；Δ表示速度与主轴之间的夹角，也就是气动总攻角；xv轴的方向与弹丸质心速度方向一致；FD表示气动阻力，方向与质心速度方向相反；FL表示气动升力，方向与质心速度方向垂直；Ma表示气动翻转力矩。尽管通过速度坐标系定义主轴方向更为直接，但是拉格朗日方程在惯性系中具有最简单的形式，因此这里的欧拉角都是相对惯性坐标系定义的。

根据坐标转换原理[17]，弹体坐标系S1t相对惯性坐标系Sg的角速度在S1t中的投影为：

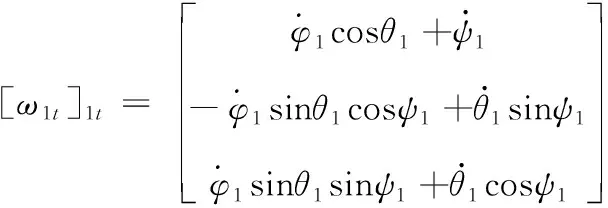
(1)

其中，符号[·]a表示向量在a坐标系中的投影。同理，可推导出与质量子系统固联的本体坐标系S2t相对惯性坐标系Sg的角速度在S2t中的投影。

按照欧拉角定义，给出x1t在惯性坐标系中的投影：

(2)

将[x1t]g简单地表示为x1。于是气动总攻角可以通过向量内积表示为：

(3)

其中，V为弹丸质心的速度。

考虑气动力矩的作用，升力FL和阻力FD分别通过升力系数Cl、零升阻力系数C0和阻力系数Cd确定；类似的，通过气动翻转力矩系数CMa可以确定气动翻转力矩Ma：

(4)

(5)

(6)

其中，Cl和Cd的量纲均为kg/m/Rad，C0的量纲为kg/m，Ma的量纲为kg/Rad。

选取φ1、θ1、ψ1、φ2、θ2、ψ2为广义坐标，由于本研究只考察弹丸的姿态运动，所以没有包含平动自由度。弹丸主轴与质量子系统主轴间的夹角α与广义坐标的关系可表示为：

cosα=cosθ1cosθ2+sinθ1cosφ1sinθ2cosφ2+

sinθ1sinφ1sinθ2sinφ2

(7)

假定质量子系统与弹丸的惯性主轴分别与各自坐标系固联且重合，且分别关于x1t轴和x2t轴对称；同时假定二者的惯性矩在y1t、z1t和y2t、z2t方向上的投影相同，定义弹丸与子系统的各主轴的惯性矩在各自坐标轴上的投影依次为I1、I2、I2和J1、J2、J2。系统总动能可表示为：

(8)

假定气流速度不变，选定θ1=0为零势能参考平面，则系统的势能可表示为：

(9)

其中，ks为两系统间的弹性系数，量纲Nm/Rad；α0为一常数，量纲为Rad，表示弹性约束的平衡位置；

由此，由L=T-U求得拉格朗日函数为：

(10)

对方程式(3)进行变分运算，得到：

(11)

在姿态运动中，由于升力FL和阻力FD不做功，对姿态角没有影响，由此可以得到总虚功的表达式为：

δW=|Ma|δΔ

(12)

则与各个广义坐标对应的广义力依次为：

(13)

(14)

Qψ1=Qφ2=Qθ2=Qψ2=0

(15)

其中，

(16)

容易看出，在式(13)～式(15)中，等式右端均包含了因式Δ/sinΔ。由于sinΔ出现在分母上，当Δ→0时，在数值计算中会导致Δ的相关项奇异。但是按照极限运动的基本规律，当Δ→0时，因式Δ/sinΔ→1。所以在下文的数值仿真计算过程中，将Δ作为自变量，为因式Δ/sinΔ编写了一个自定义函数。该函数基于级数近似的方法，当Δ趋近于零时，通过计算有限项泰勒级数给出因式的近似值。

根据拉格朗日方程原理，得到添加质量子系统后系统在空间中运动的微分方程：

(17)

(18)

(19)

(20)

(21)

(22)

联立式(17)～式(22)，即可确定包含质量子系统的弹丸的运动。

观察式(10)，发现拉格朗日函数中不显含ψ1和ψ2，对式(19)和式(22)两边积分，令：

(23)

(24)

其中，C1和C2均为常数。

为了简化论证，在弹丸与质量子系统之间添加约束φ2=φ1+π。将其代入式(7)中，得到：

cosα=cos(θ1+θ2)

(25)

于是得到∂α/∂φ1=∂α/∂φ2=0和α=θ1+θ2。于是，方程式(17)和式(20可以分别整合并改写为：

(26)

借助式(23)、式(24)和式(25)，简化式(17)～式(22)，得到简化的姿态运动模型：

(27)

(28)

(29)

其中，

μ=I2sin2θ1+J2sin2θ2

(30)

2 控制器设计

(31)

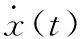
依照H∞控制设计，将式(31)整理成下面的状态依赖的类线性微分方程：

(32)

其中：w(t)为外界扰动；z(t)为输出向量；矩阵A、B1、C1是与x(t)相适应的函数矩阵。在一般的H∞控制问题中，对于给定的标量γ，令γ>0，当且仅当x(0)=0时，有如下关系：

(33)

如果系统满足上述条件，则可以称系统的L2增益小于等于γ，根据现有理论可以给出使系统稳定的哈密尔顿——雅克比不等式(Hamilton-Jacobi-Isaacs，HJIs)，根据舒尔补引理(Schur complement)，可将HJI转化为系统的有实界不等式，用于控制器的求解。具体的推导过程参考文献[18]，下面设计适用于包含质量子系统的弹丸姿态控制器。

引入H∞控制器，则状态空间中的系统方程可表示为：

(34)

其中：y(t)为输出向量；z(t)为表现控制器作用的性能向量；u是控制输入，同时也是控制器的输出信号。矩阵Cs和Ds用来平衡y(t)和z(t)，且所有向量和矩阵都具有与输入输出信号数量相适应的维数。

设计与系统相适应的状态反馈控制器K。令u=Ky，当存在标量γ，使如下有实界不等式

(35)

X>0

(36)

其中，M(x)=AX+B2W+(AX+B2W)T。当线性矩阵不等式(35)和不等式(36)有可行解W*时，u=W*(X)-1x就是系统的一个状态反馈H∞控制器。

3 数值仿真

本节运用Matlab进行数值仿真，验证提出方法的有效性。

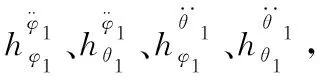
C1=C2=I6

D11=D12=D21=06×1

其中，I3,3表示3×3的单位阵的第3列；aij(i=1,…,6，j=1,…,6)分别为：

借助PBH秩判据，验证本研究提出系统的可控性和可观性。代入矩阵，可得：

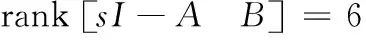
(37)

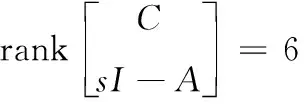
(38)

因此，文中提出的包含质量子系统的弹丸姿态运动模型满足完全可控性和完全可观性。

给定模型中相关参数(见表1)，按照式(35)中的约束条件，求解状态反馈控制器。

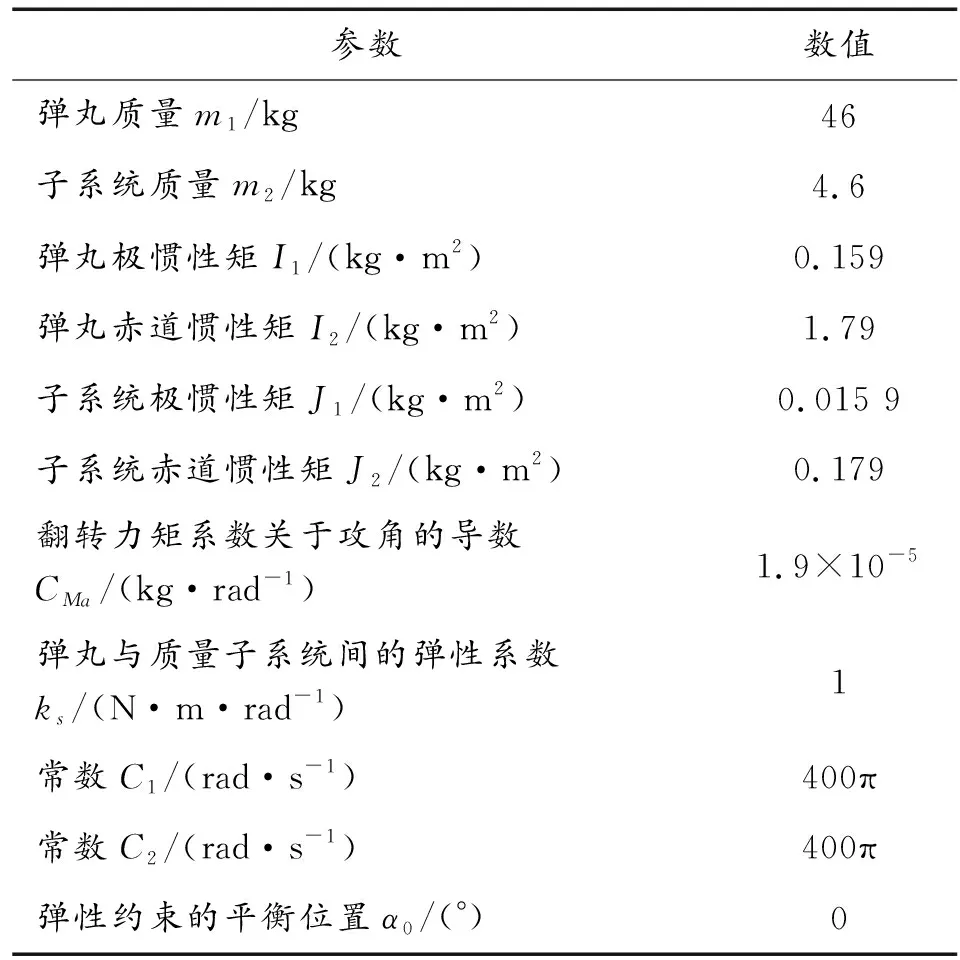
表1 相关参数

应用Matlab中的LMI工具箱求解控制器，得到控制矩阵K。仿真结果如图2所示。

由图2可以看出，添加控制器后，φ1的结果呈周期性振荡，θ1的振幅减小。由此可以看出，添加子系统后，受控弹丸的主轴偏离惯性坐标横轴的角度减小。

4 结论

基于质量调谐技术的作用原理，提出通过在弹丸内部增加一个类陀螺结构的质量子系统的方法对自旋弹丸进行姿态控制。仿真结果表明，添加质量子系统后，弹轴偏离平衡位置的幅度明显减小，验证了方法的有效性。今后将继续探究质量及系统对弹丸姿态运动的影响机理，以及将此模型用于调控弹丸姿态的非线性控制设计。

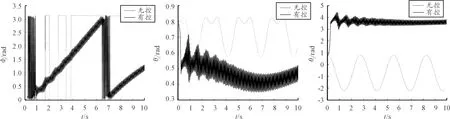
图2 添加质量子系统的弹丸的姿态运动