陶瓷靶板冲击破坏近场动力学研究
王 帅, 刘 宁, 周 飞
(南京理工大学 机械工程学院, 南京 210094)
陶瓷材料作为一种先进的高新技术材料,具有高强度、高硬度、高耐磨、耐腐蚀、抗高温以及低密度等优良的抗冲击特性,已成为一种重要的装甲防护材料。但是,陶瓷是一种脆性材料,受一次打击后容易发生破碎飞溅,靶板的抗弹性能随之降低。陶瓷材料受弹体撞击后经历材料损伤、裂纹形成扩展并最终破坏的复杂响应过程。目前对陶瓷靶板的抗冲击性能和破坏机理研究多集中在实验工作和唯象认识,深入研究陶瓷材料破坏机制已成为装甲防护领域中的研究热点。
国内外学者针对陶瓷材料冲击破坏问题开展了大量的实验研究,申志强等[1]通过设计7.62 mm穿甲子弹侵彻陶瓷靶板实验,分析了不同区域的破坏形态;Lundberg[2]通过X光摄像技术测定了钨弹作用于陶瓷靶板的界面击溃与侵彻的过渡速度。数值计算已成为研究侵彻问题的重要方法, 陶瓷材料冲击破坏数值模程,数学表达形式为一组包含空间导数的偏微分方程组,然而在面对断裂破坏不连续问题时位移偏导数并不存在,从而出现了求解困难。
一种新兴的基于非局部思想的近场动力学方法(Peridynamics,PD)从根本上解决了传统数值方法面临的求解困难,该方法采用积分形式基本方程分析求解,适用于物体连续或不连续任何区域,在模拟裂纹萌生、扩展、分离等不连续问题时表现出了独特优势[6]。
Kilic[7-8]对PD理论的本构模型、裂纹萌生及稳定性等问题进行了分析,并根据实际些情况对PD本构模型做了相应改进,使其适用于各种材料破坏分析。Wang等[9]通过改变特定的影响因素,模拟了极地船螺旋桨与冰面的接触问题,分析了叶片上铣削载荷的变化规律。秦洪远等[10]通过改进非局部键基近场动力学模型,提出了用来反应混凝土岩石类材料的近场动力学模型,分析了不同初始裂纹对构件的破坏影响规律。从模拟结果来看,近场动力学在脆性材料研究领域具有很好的实用性。
本文基于键基(bond-based)近场动力学本构模型研究陶瓷靶板冲击破坏行为,为降低模型的“网格”依赖性,采用非规则布点方法离散计算域,发展陶瓷靶板穿甲侵彻数值模拟程序,模拟陶瓷靶板损伤破坏的动态过程,分析靶板的破坏发生机理与抗弹耗能机制,并对比了不同速度下靶板损伤程度变化规律。
1 键基近场动力学基本理论
近场动力学理论中,通过虚功原理得到的近场动力学运动方程表达式为
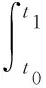
(1)
T与U分别代表物质本身具有的动能与势能,经过拉格朗日变换,推导出如下表达式
(2)
式中
t(u′-u,x′-x,t)=-t′(u-u′,x-x′,t)=
(3)
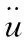
1.1 本构力函数
由微势能推出的f为内部粒子之间的本构力函数,包含材料所有本构信息,变形前后两粒子之间本构力大小与粒子之间的相对位移关系,即
(4)
式中:g为体积微元修正系数,大小取决于粒子在近场邻域中的位置,y与y′为x与x′粒子变形后位置,计算涉及材料参数被限定为固定泊松比约束下的唯一常数c,c值大小取决于材料属性,可由微势能原理推导出计算式(5),其中κ为材料体积模量;代表粒子之间相对伸长率,表达式如下
(5)
(6)
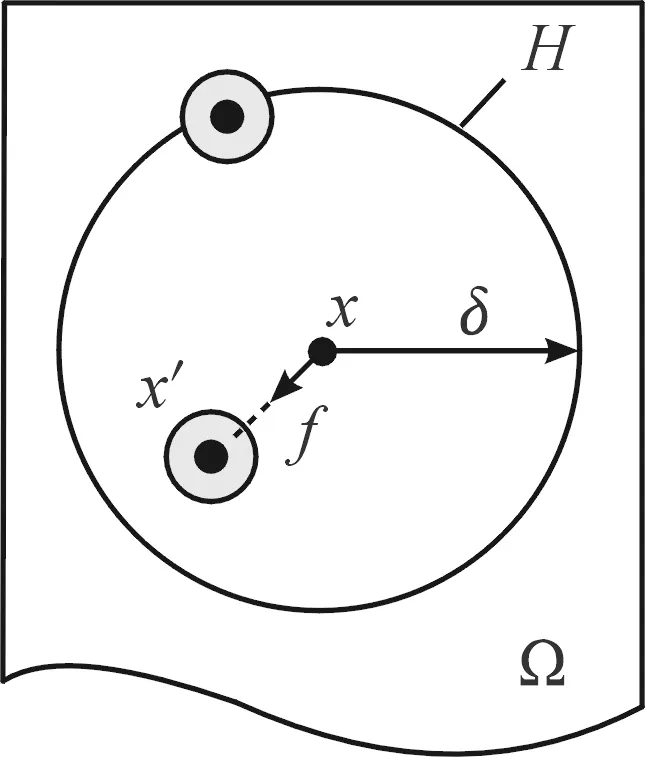
图1 近场动力学模型中粒子相互作用关系
1.2 断裂判据
当键两端粒子相对位移达到一定程度,s值超过极限相对伸长率即判定该键发生断裂,在三维问题中表征键之间极限相对伸长率的s0表达式为
(7)
式中G0为粒子之间的断裂能,在PD理论数值模拟计算中,极限相对伸长率随时间变化,表达式为
sc(t)=s0-αsmin(t)
(8)
式中:α为泊松比,smin为前一时刻粒子近场邻域中应变最小值,两粒子之间键的失效判定函数为
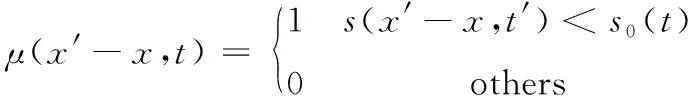
(9)
当粒子在其近场范围内与其他粒子之间键断裂数量到达一定数量,代表该粒子处发生了断裂,这个“程度”可由粒子的损伤系数表示,即由近场域内与该粒子有相互作用的失效的键的数量与总键数的比值表示,即
(10)
2 数值模型
2.1 控制方程离散形式
利用CFD前处理软件GAMBIT,对计算域进行有限元网格划分,通过提取单元节点信息实现对计算域的非规则节点划分,降低节点布置方式对PD计算结果的影响。对任一节点i,只受其近场邻域范围内节点的作用,基本方程离散形式为
(11)
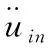
(12)
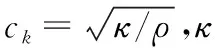
2.2 弹靶冲击接触算法
弹丸着靶后,建立弹靶接触算法实现对靶板毁伤过程,其接触模型如图2所示。将弹丸视为刚性体,弹丸运动过程中不断把靶板节点从其运动轨迹上排挤开,受排挤靶板节点速度可表示为
(13)
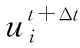
(14)
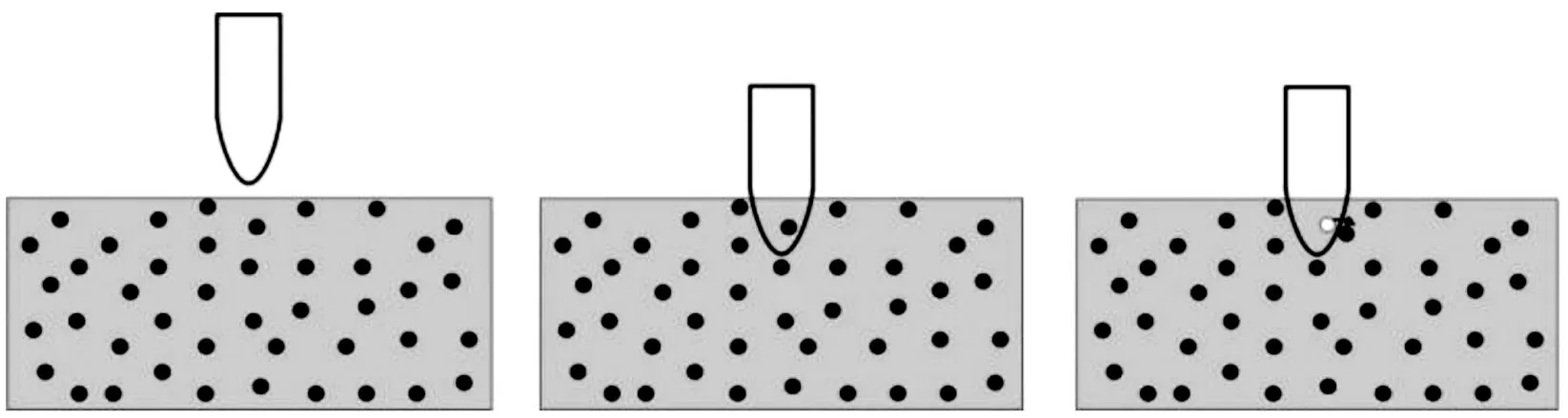
图2 弹靶接触模型
2.3 短程排斥力
在近场动力学模型中,当粒子摆脱键力束缚成为自由粒子后,为防止发生非物理穿透现象,建立短程力模型
(15)
式中dji代表j,i粒子之间短程距离,短程力只存在排斥力,cs表达式如下
(16)
短程力作用距离表达式为
dji=min{0.9||xj-xi||,1.35lji}
(17)
2.4 体积微元修正系数
考虑非局部作用积分项,如图1所示,积分域为H,部分粒子处于邻域边界,积分项体积微元不完全处于邻域内,此时需要对处于边界上的粒子体积微元进行修正,体积微元修正系数表达式如下
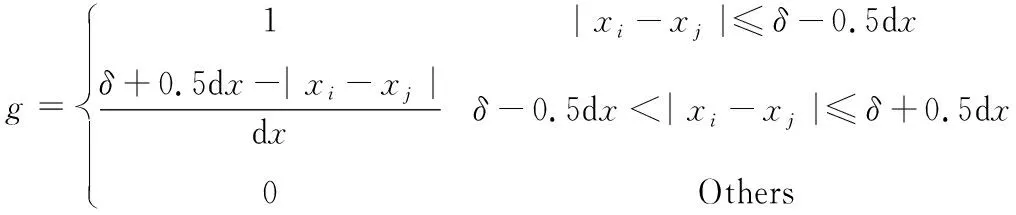
(18)
3 弹丸侵彻陶瓷靶板计算分析
建立了陶瓷靶板弹丸冲击模型,如图3所示,靶板为Al2O3陶瓷材料,长和宽均为80 mm,厚度为hc=6 mm,质量密度ρ=3 500 kg/m3,杨氏模量E=300 GPa,泊松比α=0.25。弹丸为7.62 mm穿甲弹,质量m=7.9 g,冲击速度为v=530 m/s。靶板离散为71 940个不规则分布节点,时间步长取Δt=5.7×10-8s,共计算2 000步。
图3 冲击模型
3.1 计算结果
图4为7.62 mm子弹冲击陶瓷靶板计算结果,由图可见,靶板弹着点附近大量陶瓷节点的PD键全部断裂,从靶板分离形成自由粒子,构成了粉末化破坏区域,该区域向外形成了放射性径向裂纹及环向裂纹,靶板破坏为大量的陶瓷碎片。靶板最终破坏形貌的PD计算结果与试验图像吻合较好,较好地刻画了裂纹损伤的产生发展过程,而传统有限元方法只能粗略模拟出径向与环向裂纹[5],显示了PD方法处理陶瓷材料冲击破坏问题的优势。

图4 仿真损伤结果(左)与实验[1] 损伤结果(右)
由PD方法仿真得出的环向裂纹平均半径为29 mm,接近试验结果中的半径为30 mm的环向裂纹半径,在不同厚度靶板时所得到的中心粉碎区域半径与实验中粉碎区半径如表1所示。误差e为仿真结果与试验相比较而来的误差,误差小于5%,也进一步验证了仿真结果的准确性与可靠性。
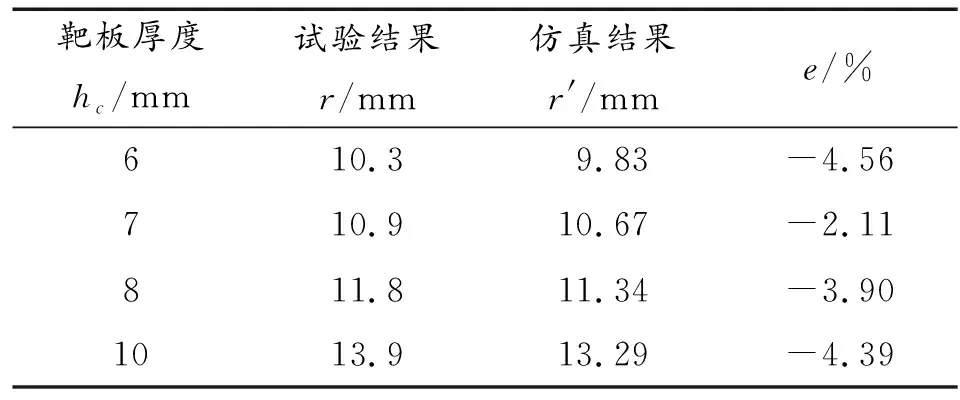
表1 粉碎区域半径试验与仿真结果对比
3.2 靶板破坏过程分析
由PD方法仿真得到靶板破坏过程,可将靶板冲击破坏过程分为3个阶段。
第一阶段,开坑阶段。子弹着靶后,弹丸在与靶板接触部位产生强制性破坏,使陶瓷表面产生界面击溃,在弹着点处形成弹坑,弹坑逐渐发展形成贯穿性损伤,如图5所示。

图5 靶板渐进损伤图
第二阶段,陶瓷锥形成阶段。陶瓷靶板由界面击溃向侵彻转变,弹丸着靶产生冲击压缩波,经边界反射后形成拉伸波,在应力波反复作用下,粒子之间相互作用逐渐弱化,键损伤的不断积累,在靶板内部形成了逐渐扩大的锥形破坏域,即陶瓷锥,如图6所示。锥形域内完全损伤粒子居多,呈粉碎性破坏,此过程靶板耗能机制主要为陶瓷的粉碎耗能。
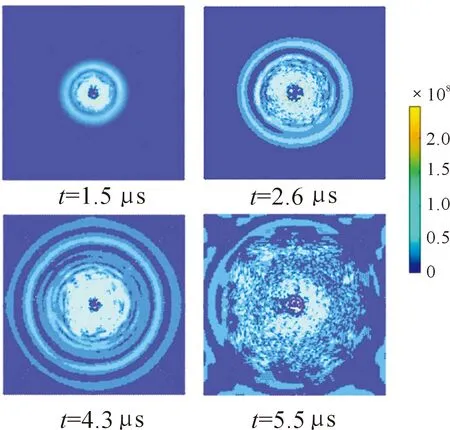
图6 应力波云图
由理论公式计算陶瓷锥形成时间[11]
(19)
式中:CL为纵波波速,vcrack为裂纹扩展速度,由文献[12]中的假设,vcrack=CL/5。得到陶瓷锥形成时间为3.6 μs,PD计算结果陶瓷锥形成时间为3.9 μs,图7为弹丸侵彻过程中剩余速度时间曲线,在0~3.9 μs期间,弹丸速度迅速降低到476 m/s,之后速度缓慢下降到465 m/s,说明在陶瓷锥形成阶段中,弹丸动能损耗最大,约占总体耗能的82%。
第三阶段,裂纹扩展阶段。伴随着弹体的运动,陶瓷锥形破坏域不再继续扩大,陶瓷锥粉碎耗能结束。与此同时靶板表面裂纹不断扩展,由于部分裂纹尖端区域能量过高,导致尖端出现次级裂纹,次级裂纹之间相互贯通形成了环形裂纹,进而使靶板发生破碎现象,此过程耗能机制主要取决于裂纹的扩展耗能。
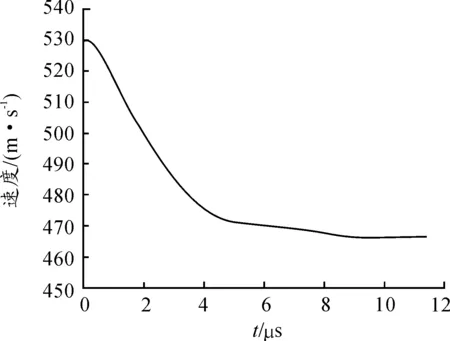
图7 弹丸剩余速度时间曲线
定义区域内完全损伤粒子数目与总粒子数比值为区域破碎程度,统计40 μs时不同区域破碎程度,其云图如图8所示。在红色区域(距中心0~5 mm,5~10 mm)分别为0.989 0与0.790 0,该区域粉化末破坏情况严重,而且可以看出靶板破片尺度与距着弹部位距离成正比,说明弹体在侵彻过程中,弹丸动能不断被吸收耗散,弹体能量不断减弱,当陶瓷靶板裂纹扩展至远端时,大尺度碎片会阻碍裂纹的扩展,使区域内破碎单元保持相对的完整性。
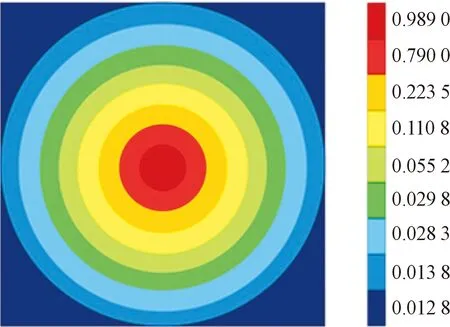
图8 不同区域破碎程度云图(40 μs)
3.3 应力波传播过程
在破坏形成的3个阶段中,应力波传播过程对破坏起主导作用。由冲击载荷产生的压缩应力波在陶瓷靶板内部传播,遇到边界后发生反射,由PD计算得到不同时刻应力波传播半径如图9所示,计算纵波波速约9 430 m/s。在冲击动力学中,应力波波速理论公式如下
(20)
其中:CL为纵波波速,λ,μ为拉密常数,得到理论纵波波速为10 142 m/s,可见PD计算结果与理论值相近,PD结果较好地再现了应力波的传播过程。
3.4 子弹速度对陶瓷靶板损伤程度的影响
为了研究不同冲击速度下靶板损伤程度,取子弹速度分别为100,200,300,400,530 m/s时,靶板厚度为6 mm,定义整个靶板完全损伤粒子数占总粒子数的百分比为靶体损伤程度,得到靶体损伤程度随子弹侵深的变化关系,如图10所示。从图中可以看出,靶板破坏速度随弹丸速度的提高而减小,这说明破坏速度只取决于靶板内部应力波的传播与叠加过程。但是随着子弹速度不断增大,靶板最终损伤量不断增加,说明子弹速度越高,靶板内部破坏越剧烈,破坏程度与子弹速度呈正相关,当贯穿完成后,损伤量增速趋于平缓,同时弹丸速度越大,贯穿完成所需时间越短。
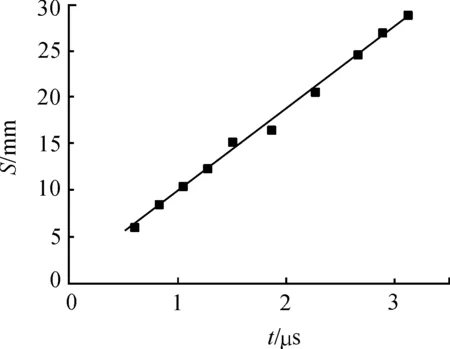
图9 应力波曲线
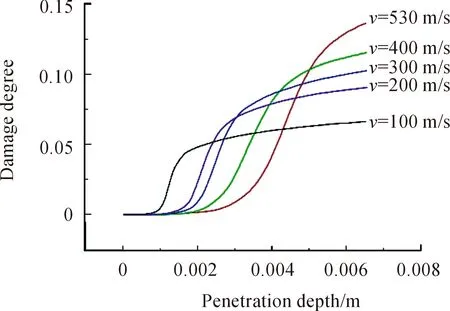
图10 不同速度下靶体损伤程度
4 结论
1) 计算模型引入了非规则布点方法,降低模型对“网格”的依赖性,模拟得到最终破坏形貌与实验结果吻合良好,所得环向裂纹平均半径接近真实情况。
2) 陶瓷靶板抗弹耗能机制主要包括陶瓷锥形成过程耗能与裂纹的扩展耗能,以陶瓷锥形成过程耗能为主,约占总体耗能的82%。
3) 在破坏过程中,冲击压缩波,与边界反射的稀疏拉伸波对陶瓷锥形成以及裂纹的形成发展起主导作用,由PD方法计算得到的应力波传播速度接近理论值10 142 m/s,陶瓷锥角形成时间接近理论计算值3.6 μs。
4) 在靶板厚度为6 mm时,冲击速度越大,靶板损伤量增幅越大,总体损伤程度越大。
5) 近场动力学理论可直接准确模拟断裂等大变形问题,为穿甲毁伤过程靶板开裂及裂纹扩展过程的数值模拟提供了新方法。

