叶片式液压摆动油缸的动态特性仿真研究*

李 昭，谢良喜，罗 刚，罗中正，加 闯

(武汉科技大学 机械自动化学院，武汉 430081)

0 引言

摆动油缸输出力矩很大，当驱动大负载时，要求有较高的低速平稳性和较高的动态品质。摆动油缸在流量或负载出现变化时，就会产生转子速度变化和油腔压力变化的瞬态过程。摆动油缸的动态特性分析就是对这一瞬态过程中转子速度和油腔压力变化进行分析。如果摆动油缸没有好的动态性能，就会出现运行不稳定的现象，甚至出现不连续工作的情况，因此研究摆动油缸的动态特性是非常必要的。

薛晓虎[1]分析了起重运输机械阀控液压马达回路的动态性能，介绍了固有频率和阻尼比对系统动态性能的影响。吴若麟[2]通过优化自伺服缸结构改变固有频率从而提高响应速度，但忽略了阻尼比对动态特性的影响。杨国来[3]通过推导传递函数，对阀控液压马达系统进行动态特性仿真研究，发现加入PID控制可以提高系统的抗负载扰动性能。徐海军[4]对某推进器中的液压摆动关节进行了动力学建模，并通过Bode图研究了该关节的动态特性。王大伟[5]利用泵控液压马达系统的相关流量方程，通过Simulink生成仿真模型研究了系统动态特性。虽然国内学者对一些液压马达和摆动机构的动态特性进行了分析，但由于摆动油缸密封系统复杂，缺少综合考虑固有频率和阻尼比对摆动油缸动态特性影响的理论研究。

本文在已解决摆动油缸密封系统可靠性[6]的基础上，运用改进的摆动油缸动态特性数学模型对摆动油缸动态特性进行分析研究，比较了数学模型改进前后的角速度响应曲线和高压腔压力曲线，并指出影响摆动油缸响应快速性和运动平稳性的主要因素。

1 摆动油缸结构与工作原理

摆动油缸是液压系统的执行元件，结构组成包括：缸体定子(定子)、缸体转子(转子)、端面密封、叶片密封、叶片支撑、盖板等，如图1所示。其中密封系统包括：端面密封和叶片密封，且两个密封之间过盈配合。叶片密封、定子和转子将摆动油缸分为了两个密封腔，密封腔互不相通。端面密封安装于缸体两端位于叶片密封两侧，与叶片密封保持紧密接触，叶片密封安装于叶片支撑槽中，叶片支撑槽分为定子叶片支撑槽和转子叶片支撑槽，分别固定于定子内壁与转子外壁上。摆动油缸的进油孔与出油孔分别设置在定子叶片支撑两侧。当两个密封腔分别输入高低压油液时，两个密封腔之间的压力差作用于相应的转子叶片密封，而转子的叶片会将此作用力转化为转子上叶片支撑槽的压力，进而推动转子旋转，输出力矩。当变换两个密封腔输入的介质油压力时，就能形成摆动油缸的来回旋转运动，即摆动。

1.端面密封 2.定子 3.转子 4.叶片 5.盖板图1 摆动油缸结构

2 数学模型

摆动油缸-负载系统如图2所示，工作腔通入高压油，推动转子克服外负载逆时针转动，低压腔中的油液则经油管和液压阀进入油箱。为简化模型，设摆动油缸低压腔与油箱直接相通，即P2=0。摆动油缸的数学模型由其工作时油腔的流量平衡方程与转子的力矩平衡方程组成。

图2 摆动油缸动态分析简图

摆动油缸工作时油腔的流量平衡方程为[7]：

(1)

其中，b为叶片高度(mm)，ω为摆动油缸角速度(rad/s)，R为摆动油缸定子内腔半径(mm)，r为转子半径(mm)，λc为摆动油缸泄漏系数[m3/(s·Pa)]，Vc为摆动油缸油腔和输油管油液总体积(m3)，K为油液体积弹性模量(Pa)。

改进后的摆动油缸转子力矩平衡方程为：

(2)

对式(1)和式(2)作Laplace变换并整理得：

(3)

(4)

以Q(s)为输入，ω(s)为输出，可作出摆动油缸的方框图，如图3所示。

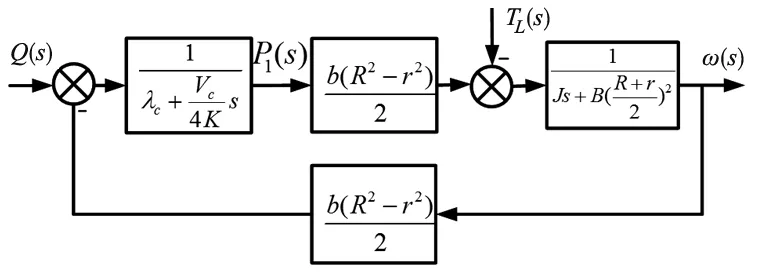
图3 摆动油缸动态方框图

摆动油缸的输入为流量和外负载，输出为角速度和力矩，因工作腔的工作压力反映输出力矩，故输出为摆动油缸转子角速度及工作腔压力。

由式(3)、式(4)可求得摆动油缸输出ω(s)为：

(5)

其中，D为摆动油缸工作腔单位弧度体积排量，系数A、B、C、D、E分别为：

由式(3)、式(4)可求得摆动油缸输出P1(s)为:

(6)

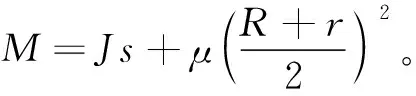
由式(5)、式(6)可求得摆动油缸固有频率ωn为：

(9)

叶片式液压摆动油缸阻尼比ζ为：

(10)

3 摆动油缸的Simulink建模

摆动油缸的各个参数如表1所示。

表1 摆动油缸参数表

Simulink是MATLAB中建立和分析动态系统模型的工具箱，具有图形化的操作界面，通过简单操作即可生成繁琐的仿真模型[8-9]。根据图3中摆动油缸方框图，利用MATLAB建立摆动油缸仿真模块图，如图4所示。

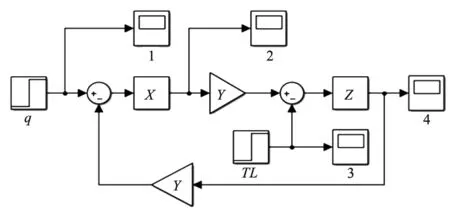
图4 摆动油缸仿真模块图

图中X、Y、Z分别为：

Y=0.00023

设置仿真时间为0.2s，当时间为t=0时对摆动油缸输入一阶跃流量q=4.2L/min,同时输入阶跃负载力矩TL=300N·m。

摆动油缸的动态特性数学模型改进前后的仿真结果如图5、图6所示。

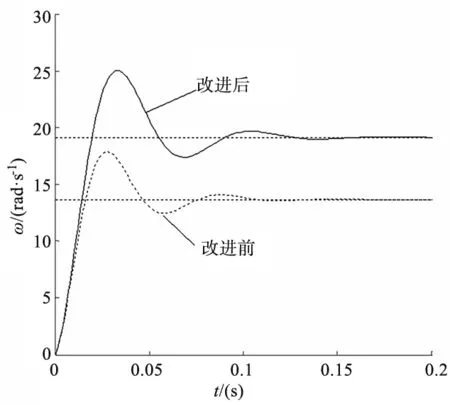
图5 角速度响应曲线

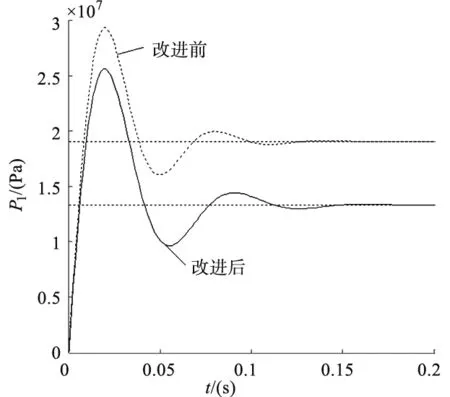
图6 高压腔压力曲线

可以看出，摆动油缸在阶跃流量和阶跃负载力矩的作用下，数学模型改进后的转子角速度从零开始上升，经过振荡最终稳定在19.1rad/s，而改进前的转子角速度最终稳定在13.7rad/s；数学模型改进后的高压腔压力经过振荡最终稳定在13.3MPa，而改进前的高压腔压力最终稳定在19MPa，可见数学模型中粘性阻尼产生的力矩对分析摆动油缸的动态特性的影响较大，因此对摆动油缸动态特性数学模型中的力矩平衡方程的改进是很有必要的。数学模型改进后的摆动油缸性能指标见表2。

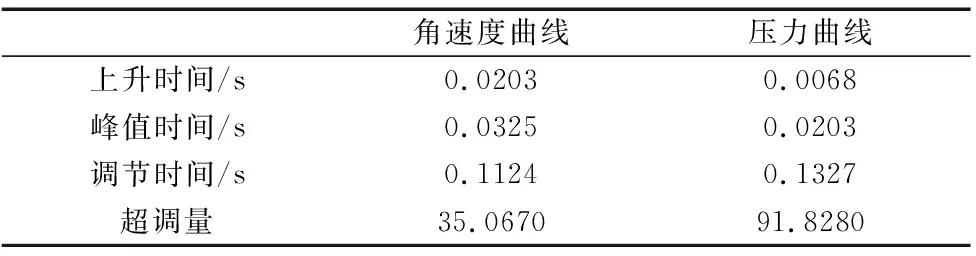
表2 摆动油缸的性能指标

3.1 响应快速性和运动平稳性分析

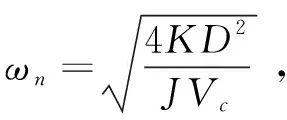
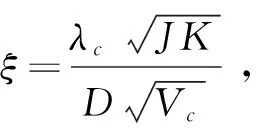
3.2 摆动油缸动态性能优化

由3.1分析可知，减小摆动油缸油腔与输油管油液总体积可同时增大摆动油缸的固有频率和阻尼比。通过优化减小输油管长度，使Vc由2×10-4m3减小到1.6×10-4m3，对比优化前后的角速度响应曲线和高压腔压力曲线如图7、图8所示，优化后摆动油缸性能指标见表3。

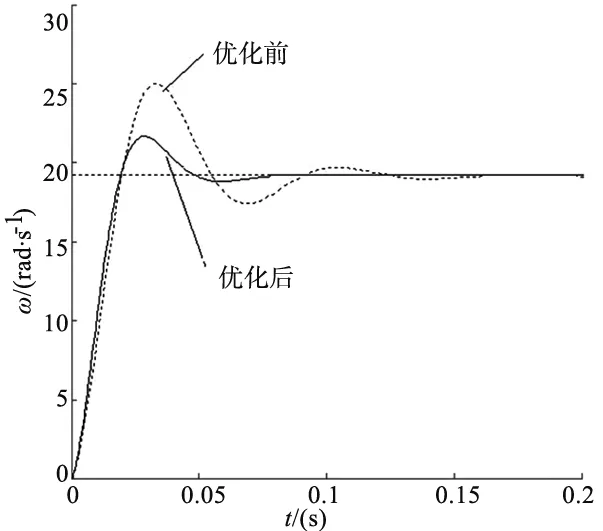
图7 角速度响应曲线

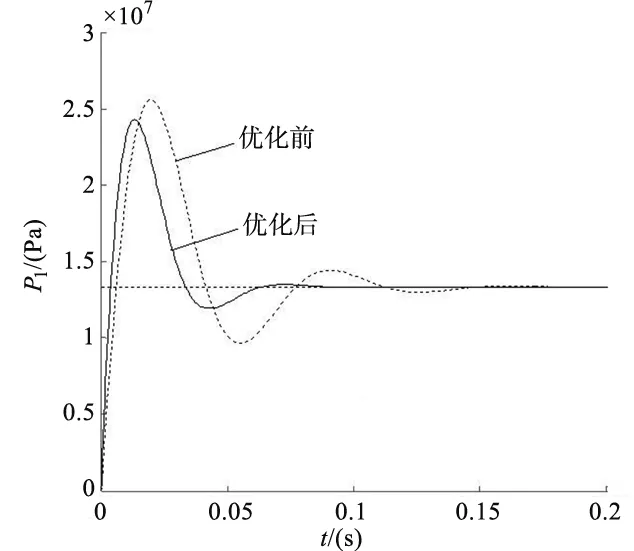
图8 高压腔压力曲线

角速度曲线压力曲线上升时间/s0.01940.0040峰值时间/s0.02800.0133调节时间/s0.04400.0581超调量13.115682.3238

优化后(表3)角速度曲线、压力曲线的上升时间、峰值时间、调节时间均比优化前(表2)小，表明优化后响应速度提升，并且优化后的超调量也由原来的91.828减小到82.3238，表明优化后稳定性提高。

4 结论

主要对摆动油缸动态特性数学模型进行了改进，并研究了摆动油缸的动态特性，最终可以得到以下结论：

(1)对比摆动油缸动态特性数学模型改进前后的动态特性曲线，发现改进前与改进后动态特性曲线差异较大，验证了数学模型改进的必要性。

(2)通过增大摆动油缸的固有频率可以提高其响应速度，增大摆动油缸阻尼比可以减小摆动油缸超调量，增强其稳定性。

(3)通过减小摆动油缸油腔与输油管油液总体积对摆动油缸动态性能优化，优化后的性能指标表明摆动油缸动态性能得到较大提升。