2024铝合金铣削加工表面残余应力仿真研究

郑耀辉，赵明月，刘 娜，王明海

(1.沈阳航空航天大学 航空制造工艺数字化国防重点学科实验室，沈阳 110136；2．中国航发沈阳黎明航空发动机有限责任公司，沈阳 110000)

0 引言

随着我国航空工业的飞速发展，航空用大型铝合金整体结构件因具有强度高、自身重量轻、承载能力大及抗破坏能力强等特点而在新一代航空产品中得到广泛应用。但由于整体结构件在铣削加工过程中普遍存在加工变形的问题，抑制乃至消除加工变形以提高整体结构件的加工精度己为大家所关注。研究表明已加工表面残余应力对零件的使用性能有着重要的影响[1-5]，残余拉应力会降低零件的疲劳强度，而残余压应力却恰恰相反，由于各部分的残余应力分布不均匀还会使工件发生变形，影响工件的形状精度和尺寸精度。因此，研究加工表面残余应力对保证零件表面质量有重要意义[6]。刘文文和刘长毅[7]建立了钛合金二维正交切削的热力耦合有限元仿真模型，研究了在不同切削条件下加工残余应力的分布规律，覃孟扬[8]研究了基于预应力的切削加工表面的残余应力，利用有限元软件进行正交模拟，研究预应力和切削参数对表面残余应力影响，孙雅洲[9]等人利用有限元模拟的方法对铝合金Al2A12进行了研究，分析了切削加工表面残余应力的分布及其影响因素，孙会来[10]、Jomaa W[11]等利用ABAQUS对7075-T651铝合金进行二维正交切削仿真，但仿真模型与实际切削过程有一定误差，国内外对切削加工表面残余应力的研究主要通过有限元分析和切削试验的方法建立残余应力的预测模型，研究单工艺参数对表面残余应力的影响，没有对切削参数相关的优化和切削亚表面进行进一步的研究[12-13]。2024铝合金是Al-Cu-Mg系可热处理强化的变形铝合金，综合性能较好，常用状态为T4态，广泛用于飞机蒙皮、骨架、肋梁、隔框等高强度结构件，对2024铝合金的研究主要集中在材料热处理和对其组织性能影响方面，对其切削加工及切削参数研究较少。

论文利用专业有限元切削软件对2024铝合金进行切削仿真，研究切削表面残余应力和亚表面残余应力的变化，并建立正交试验和单因素试验研究切削参数对切削表面残余应力的影响，进行参数优化。

1 有限元模型的建立

有限元仿真模型如图1所示，在铣削的实际过程中，刀具作进给运动，并伴随机床主轴的转动所以实际上铣刀同时作旋转和进给运动，运动轨迹是一条摆线，相邻的两个刀齿运动轨迹所围成的部分就是一个刀齿的切削面积，虽然切削厚度是连续变化的，但由于每齿进给量比较小，刀具的旋转速度又很高，所以其厚度变化非常小，可以将厚度连续变化的切削层简化成均匀厚度的等效切削层。[14]

工件材料选取材料库中的2024-T42材料，刀具选取刀具库中的硬质合金刀具，刀具直径20mm，刀尖圆弧半径0.02mm，前角18°，后角10°。利用软件中的自适应网格划分技术，工件和刀具网格划分的最大尺寸为0.1mm，最小为0.02mm。铣削参数为铣削速度750m/min，每齿进给量0.1mm/z，铣削深度2mm，铣削宽度6mm，工件和刀具的初始温度为20°，切削长度10mm，采用干铣削的加工方式。

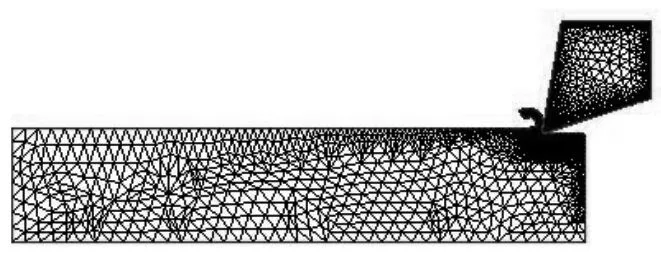
图1 2D铣削仿真模型

2 正交试验

如表1所示模拟采用四因素三水平的正交试验方案，根据四因素三水平的正交试验方案设计要求,选用不同的切削速度、每齿进给量、切削宽度和切削深度为研究的对象，对模拟结果(加工表面残余应力)进行相关的方差分析计算，研究切削参数对表面残余应力和铣削温度的影响。然后根据模拟结果，利用多元线性回归法来推导加工表面残余应力的预测公式[15]。最后通过实验，验证模拟和预测公式的准确性。

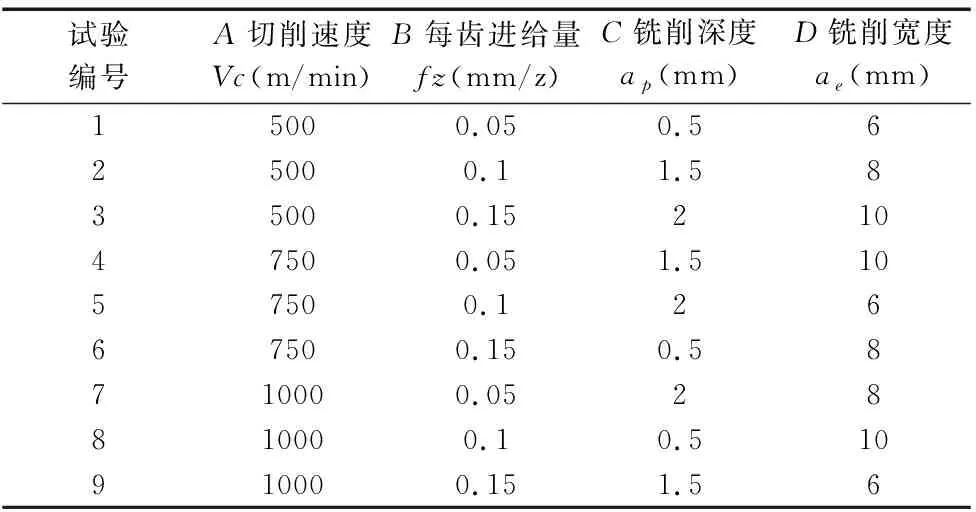
表1 正交试验设计

3 加工残余应力仿真结果分析

3.1 切削表面残余应力力分析

图2计算了切削速度Vc=750m/min，每齿进给量fz=0.1mm/z，切削深度ap=2mm，切宽ae=6mm时残余应力随表面深度的变化曲线，加工表面残余应力开始表现为残余拉应力，因为最外表面残余应力主要受温度影响，沿着深度方向在0～0.08mm的厚度变化范围内残余拉应力迅速降低，然后过渡为压应力，随着深度的增加温度对表层残余应力的影响越来越小，切削表面的残余应力主要受挤压效应的影响，压应力经历一个先增大后减小的过程，最后接近于0MPa，其中σmax为119MPa，σimin为-65MPa。

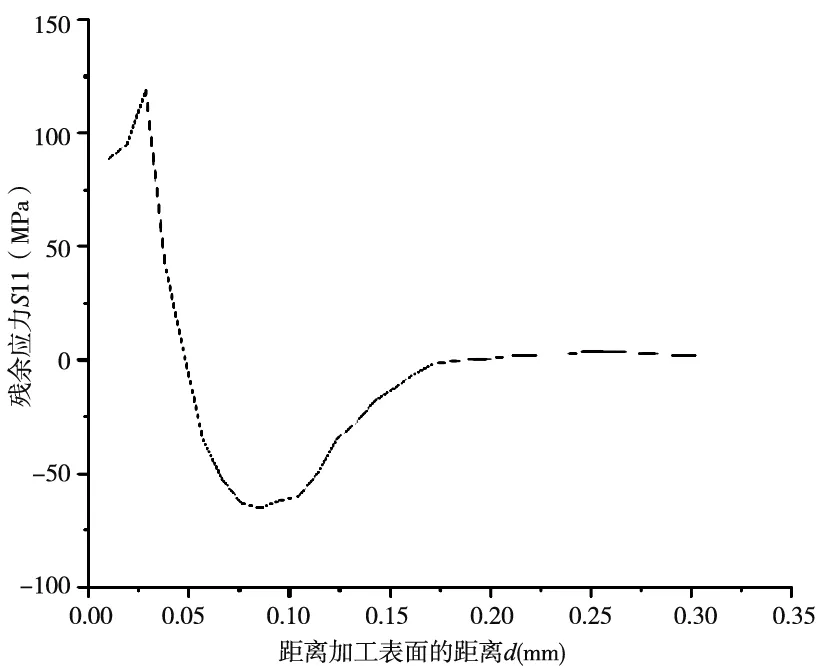
图2 切削加工残余应力仿真曲线

3.2 正交试验仿真结果分析

得到的仿真数据如表2所示，采用直观分析法对仿真结果展开分析，仿真结果分析表3为σimax数据分析，表4为σimin的数据分析，表5为T的数据分析。表中K1、K2、K3表示每个因素一个水平的求和，k1、k2、k3表示K1、K2、K3的平均值，R表示极差。

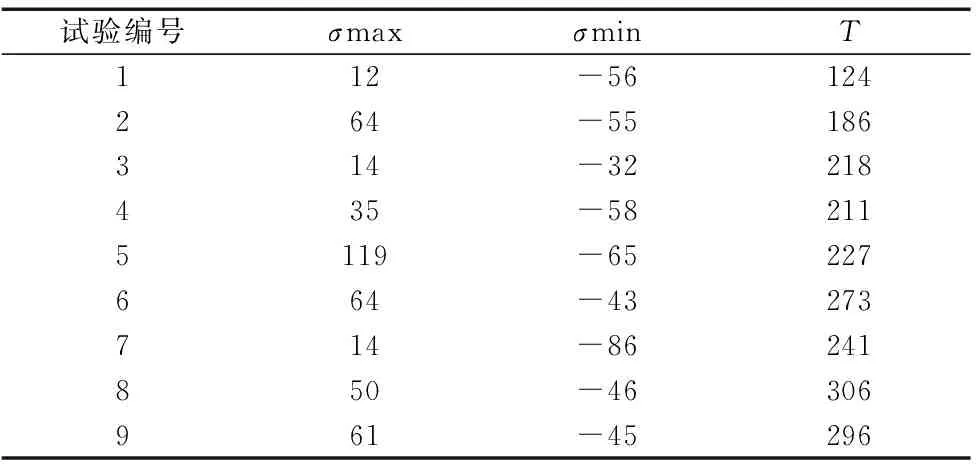
表2 仿真结果

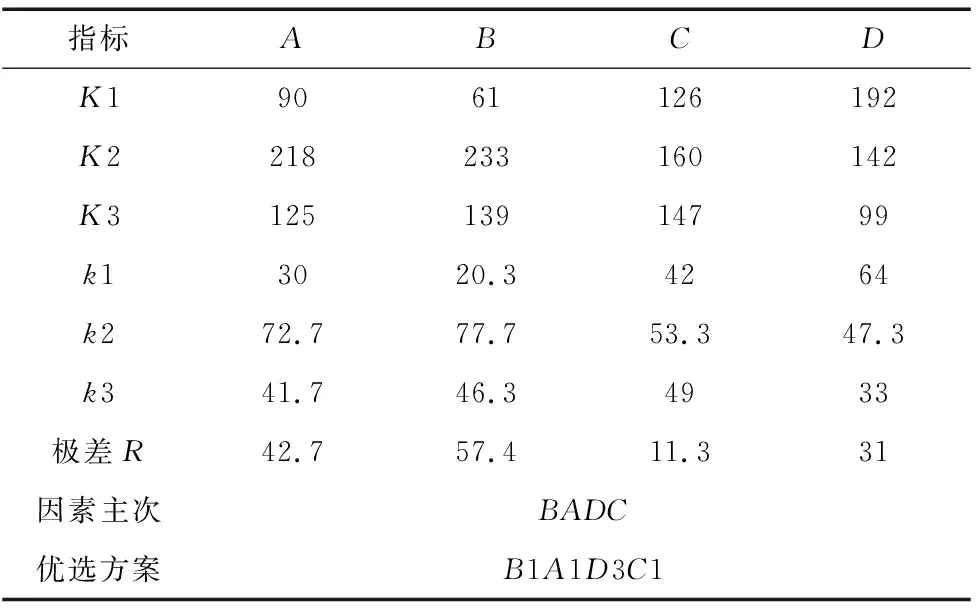
表3 σmax仿真分析

从表3可以看出，每齿进给量和铣削速度对σmax影响较为显著，因素主次为B>A>D>C，因此优选方案为B1A1D3C1，即每齿进给量0.05mm/z，切削速度500m/min，铣削宽度10mm，铣削深度0.5mm。

表4 σmin仿真分析

从表4可以看出，每齿进给量和铣削宽度对σmin影响较为显著，因素主次为B>D>C>A，因此优选方案为B3D3C1A1，即每齿进给量0.15mm/z，铣削宽度10mm,铣削深度0.5mm，切削速度500m/min。

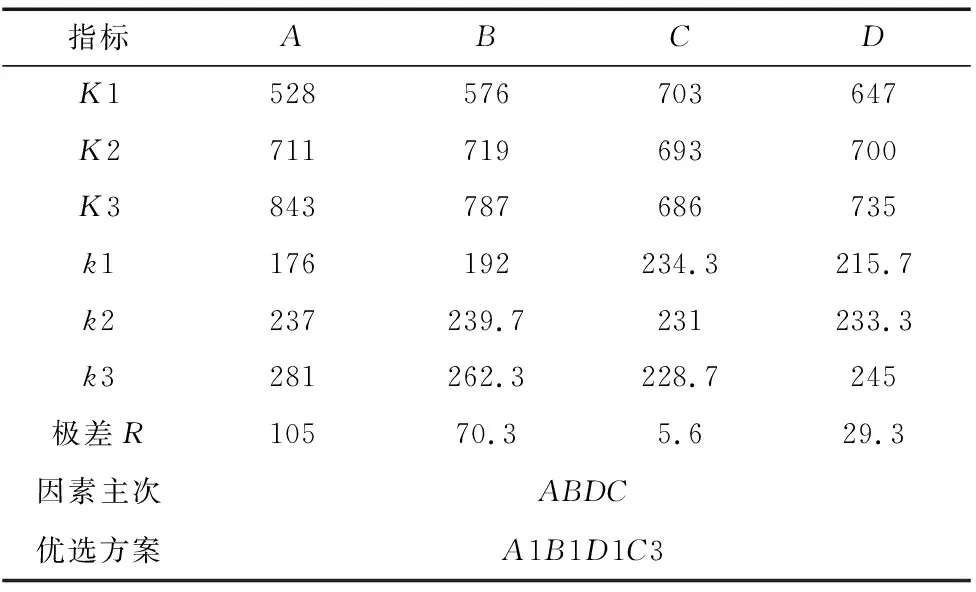
表5 T仿真分析

从表5可以看出，铣削速度和每齿进给量对T影响较为显著，因素主次为A>B>D>C，因此优选方案为A1B1D1C3，即切削速度500m/min，每齿进给量0.05mm/z，铣削宽度6mm,铣削深度2mm。

综上所述，为了控制加工表面残余拉应力的极值，选取切削速度500m/min、每齿进给量0.05mm/z、铣削深度0.5mm和铣削宽度10mm为最优参数，为了控制加工亚表面残余压应力的极值，选取切削速度500m/min、每齿进给量0.15mm/z、铣削深度0.5mm和铣削宽度10mm为最优参数。

3.3 残余应力预测公式

根据上面模拟的一系列数据，通过多元回归方程来推导一个残余应力极值的经验公式，假定该经验公式为：

σmax=Capn1aen2fn3vn4
σmin=Capn1aen2fn3vn4

C是系数为固定值，n1，n2，n3，n4分别是ap，ae，f，v的指数，对公式两边同时取对数：

lnσmax=lnC+n1lnap+n2lnae+n3lnf+n4lnv或者Y=n0+n1X1+n2X2+n3X3+n4X4

经验公式变成了多元线性方程，通过求n0，n1，n2，n3，n4的值来确定经验公式。

把正交方案中的数代入公式并利用MATLAB对试验结果进行多元线性分析，得出加工残余应力的经验公式为：

σmax=7.5716ap0.0201ae-0.8129f0.8203v0.7928
σmin=5.931ap0.1051ae-0.3935f-0.4353v0.2925

3.4 切削加工残余应力试验验证

为了验证仿真结果和经验公式的准确性，试验选取表6中的三组切削参数在立式加工中心进行铣削试验，如图3所示，利用小孔法测量表面残余应力[16-17]，正值代表残余拉应力，负值代表残余压应力，最后将切削参数代入残余应力预测公式，得到残余应力的公式计算结果，分别计算仿真，公式计算，实验值间的误差。

表6 对比试验方案

(a) 工件铣削加工 (b) 残余应力测量 图3 铣削加工和表层残余应力测量试验

试验值公式计算值模拟值σp/MPaσc/MPa相对误差σs/MPa相对误差6759.611%5912%4440.57.9%409%2220.66.3%214.5%

实验结果和相关计算结果见表7。从中可以看出有限元模拟值、公式计算值和实验值都存在一定的误差，但有限元模拟值最大误差率为12%，公式计算值最大误差率为11%,通过结果对比证明上面建立的有限元模型基本正确；在其他切削条件相同的情况下，通过公式来预测残余应力是可行的。

仿真结果与试验结果有一定误差，这是因为仿真是在较为理想的环境中进行，而试验过程中测得的残余应力是初始残余应力和切削加工表面残余应力叠加后的合力，同时又受到机床和装夹等的影响，就整体而言仿真结果与试验结果较为吻合，能够较为准确的预测表面残余应力极值的大小。

4 单因素对表面残余应力的影响

为了得到单一铣削参数对切削表面残余应力的影响规律，采用单因素试验法，切削速度、每齿进给量、铣削深度和铣削宽度每个影响因素选出3个数值，进行仿真研究，铣削工艺参数如表8所示。

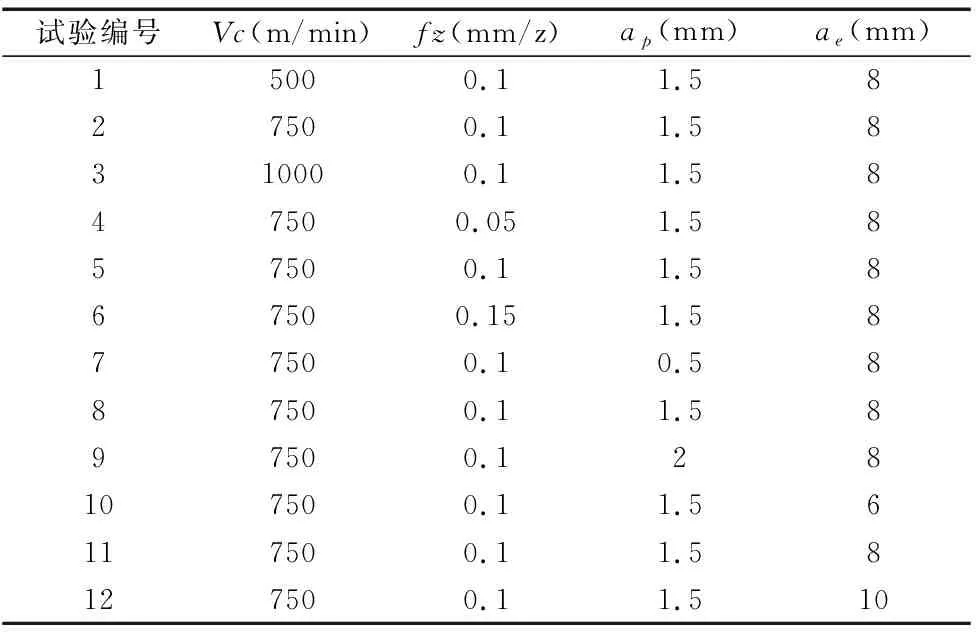
表8 铣削参数

4.1 切削速度对切削表面残余应力的影响

切削速度对切削表面残余应力的影响曲线如图4所示。当切削速度增大时，切削温度升高，由热应力引起的残余应力起主导作用，从而使表面产生残余拉应力，并随着切削速度的提高而增大；同时次表层的残余压应力有减小的趋势，残余压应力有向残余拉应力转化的趋势。

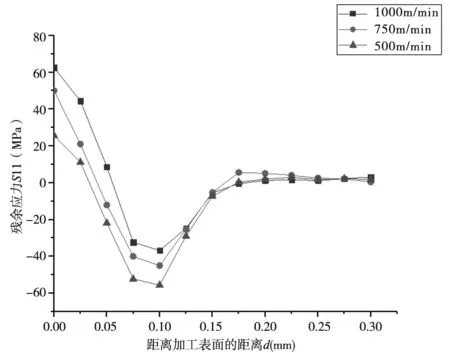
图4 切削速度对表面残余应力的影响曲线

4.2 每齿进给量对切削表面残余应力的影响

每齿进给量对切削表面残余应力的影响曲线如图5所示。随着每齿进给量的增大，表面残余拉应力增大，次表层残余压应力减小，这是因为进给的增大使单位时间内材料的切除量增多，刀具与工件之间的摩擦增大，产生的热增多，由热塑性变形造成的残余拉应力增大，使残余压应力向拉应力转变。

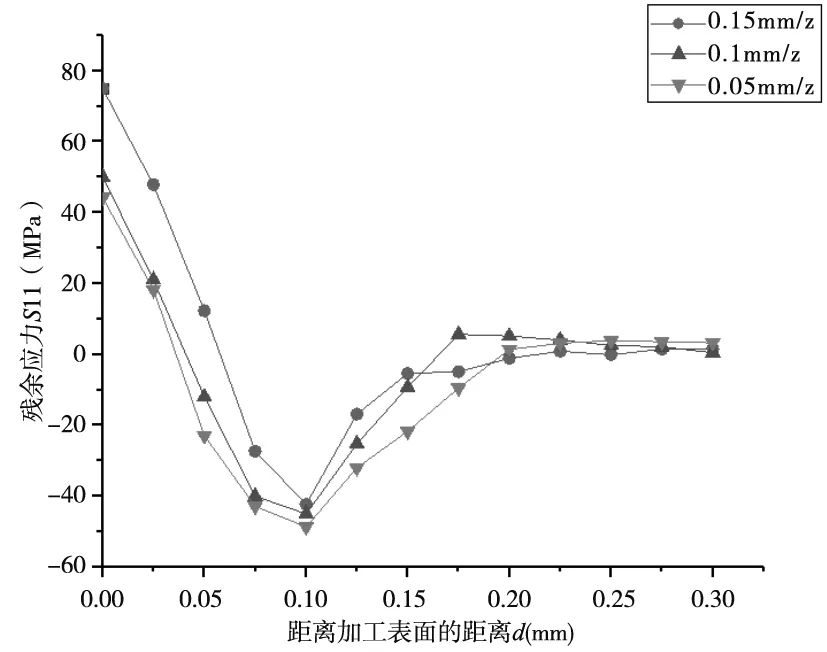
图5 每齿进给量对表面残余应力的影响曲线

4.3 切削深度对切削表面残余应力的影响

切削深度对切削表面残余应力的影响曲线如图6所示。切削深度对残余应力的影响不太显著，变形力会随着切削深度的增大而增大，但变形系数却相反，随着切削深度的增加而减小，导致摩擦系数减小，所以切削深度对表面残余应力的影响较小。

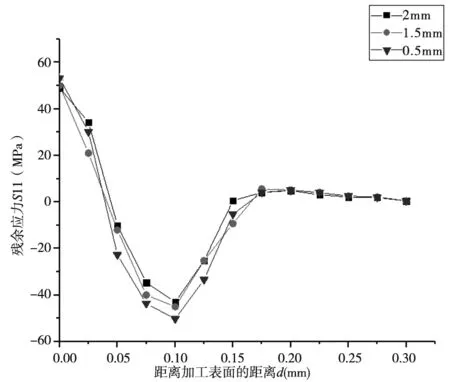
图6 切削深度对表面残余应力的影响曲线

4.4 切削宽度对切削表面残余应力的影响

切削宽度对切削表面残余应力的影响曲线如图7所示。随着铣削宽度的减小，金属的去除率减小，使形成切屑的阻力减小，使塑性凸出效应及热塑性变形不明显，由后刀面产生的挤光效应处于主导地位，所以工件表层残余拉应力向残余压应力转化的趋势。

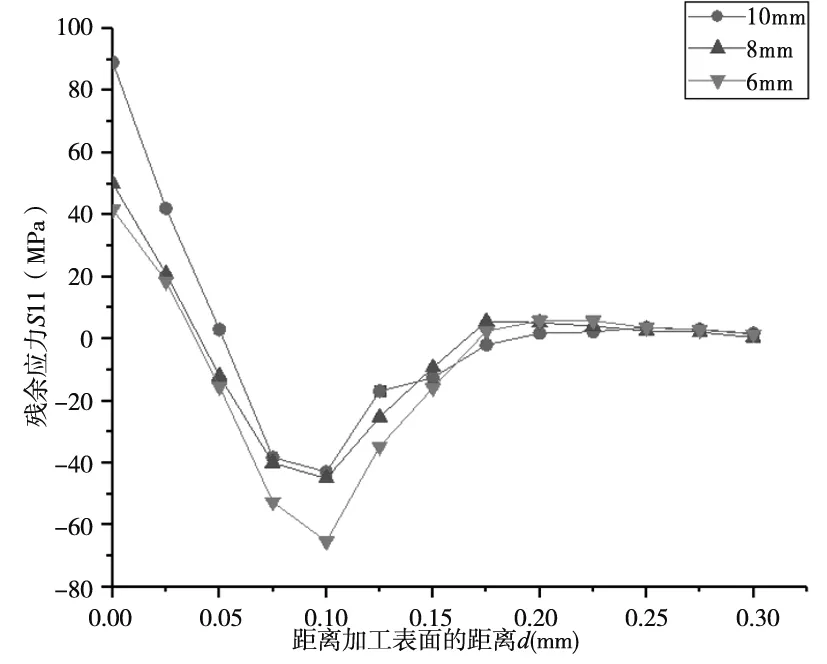
图7 切削宽度对表面残余应力的影响曲线

根据以上分析，切削速度、每齿进给量和铣削宽度对表面残余应力力的影响较大，切削深度影响较小。因此，在实际生产条件允许情况下，为了控制表面残余应力，提高加工质量，在铣削2024铝合金时，应采用较低的切削速度，较低的进给量、铣削深度和铣削宽度。

4.5 铣削参数对铣削温度的影响

铣削参数对铣削温度的影响规律曲线如图8所示。从图中可以看出，铣削温度随着切削速度的升高而增大，温度从180℃增大至286℃，增加了106℃，材料内部应变率随着切削速度的增大而增大，造成工件材料温度也上升。铣削温度随着每齿进给量和铣削宽度的增加而变大，分别增大了71℃和39℃，铣削深度对铣削温度的影响极小。

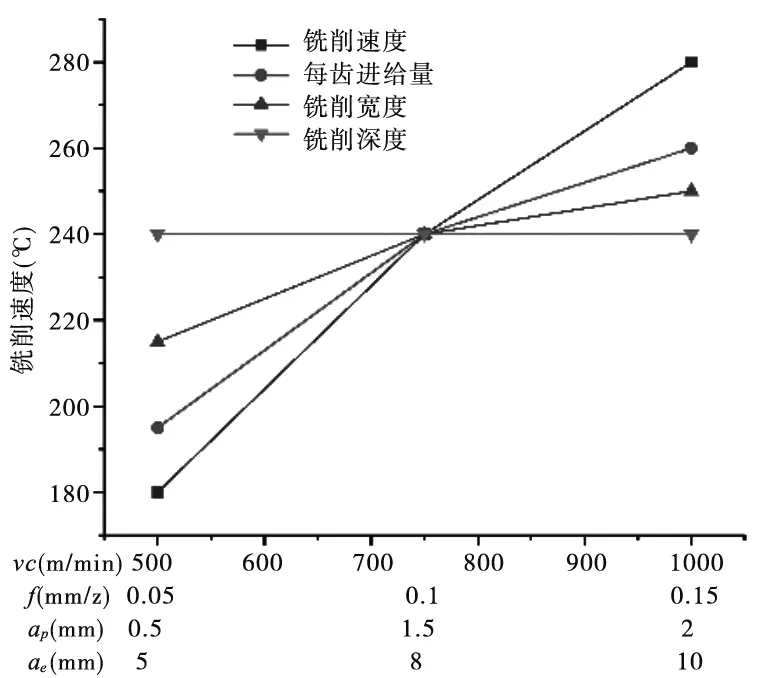
图8 铣削参数对铣削温度的影响曲线

5 结论

通过有限元分析软件对2024-T42铝合金的铣削过程进行仿真和铣削试验，可以得出以下结论：

(1)论文使用的有限元模型能够较为准确的预测2024铝合金的切削表面残余应力，切削加工试验结果与有限元模拟结果预测公式计算结果基本一致验证了有限元模型和预测公式的正确性。

(2)通过正交试验选出最优的铣削工艺参数，为了控制表层残余应力的极值，选取每齿进给量0.05mm/z，切削速度500m/min，铣削宽度10mm，铣削深度0.5mm；为了控制亚表面残余应力的极值，选取选取切削速度500m/min、每齿进给量0.15mm/z、铣削深度0.5mm和铣削宽度10mm为最优参数。

(3)建立了以切削参数为变量的加工表面残余应力极值预测公式，并进行了切削加工试验，残余应力试验结果与预测公式计算结果基本一致，验证了预测公式的正确性。

(4)切削深度对表面残余应力的影响较小，表面残余应力力随切削速度、每齿进给量、铣削宽度的变大而升高，因此，在实际生产条件允许情况下，为了控制表面残余应力，提高加工质量，在铣削2024铝合金时，应采用小的切削速度，小的进给量、铣削深度和铣削宽度，铣削温度随每齿进给量、切削速度和铣削宽度升高而变大，铣削深度对铣削温度的影响极小。