系统机械能守恒定律在连接体模型中的应用

四川

连接体是由若干个物体通过轻绳、轻杆等连接起来的系统，其涉及相互作用的物体多、受力和运动情况复杂，因此该类问题综合性较强，解决此类问题除了运用整体、隔离法外，还可以用系统机械能守恒定律求解。下面笔者从以下三种模型进行探讨。

一、速率相等的连接体模型

该模型的特点是两个物体通过不可伸长的轻绳连接，其速度方向均沿着绳且两物体速率相等。这种模型中单个物体机械能一般不守恒，但是系统的机械能守恒。

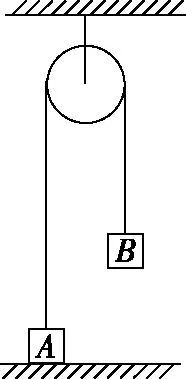
图1

【例1】如图1所示，物块A和B通过一根轻质不可伸长的细绳连接，跨放在质量不计的光滑定滑轮两侧，质量分别为mA=2 kg、mB=1 kg。初始时A静止于水平地面上，B悬于空中。先将B竖直向上举高h=1.8 m(未触及滑轮)然后由静止释放，一段时间后细绳绷直，A、B以大小相等的速度一起运动，之后B恰好可以和地面接触。取g=10 m/s2，空气阻力不计。求：

(1)B从释放到细绳刚绷直时的运动时间t；

(2)A的最大速度v的大小；

(3)初始时B离地面的高度H。

【答案】(1)t=0.6 s (2)v=2 m/s (3)H=0.6 m

(2)设细绳绷直前瞬间B速度大小为vB，则vB=gt=6 m/s。又因为细绳绷直瞬间，张力远大于A、B的重力，所以系统动量近似守恒，故mBvB=(mA+mB)v，解得A、B的速度v=2 m/s。然后A、B一起做匀减速运动，v=2 m/s即为A的最大速度。

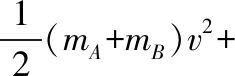
【点评】(1)细绳绷紧的瞬间系统动量近似守恒，但机械能不守恒。细绳绷直后A、B一起运动，A、B两物块组成的系统只有动能与重力势能之间的转化，所以系统机械能守恒。(2)选择表达式ΔE减=ΔE增进行求解，这样可以不必选择零势能参考平面，给解题带来了方便。

二、分速度相等的连接体模型

该模型的特点是A、B两个物体通过轻绳(或轻杆)相连，其中A物体的速度方向不沿绳(或杆)，B物体的速度方向沿绳(或杆)，我们可以将A物体的速度进行正交分解，这样其沿绳(或杆)的分速度大小就与B物体的速率相等了。这种模型中单个物体机械能一般也不守恒，但是A、B系统的机械能守恒。

【例2】如图2所示，有一半径为R的半圆形圆柱面MPQ，质量为2m的球A与质量为m的球B用不可伸长轻绳连接后挂在圆柱面边缘，现将球A从边缘M点静止释放，若不计一切摩擦，求：球A沿圆柱面滑到最低点P时速度大小及此时球B的速度大小。

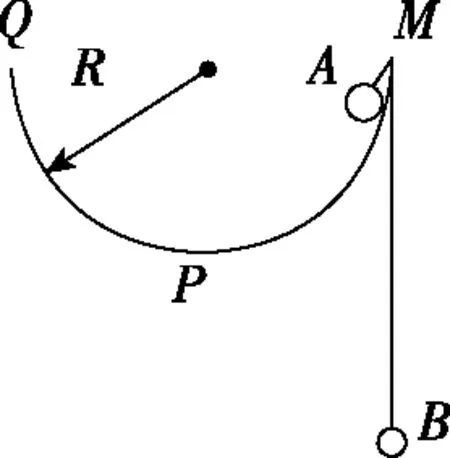
图2

图3

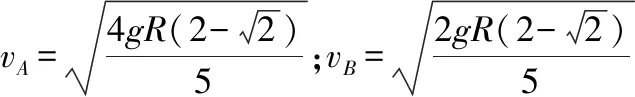
因为A、B系统只有重力做功，所以系统的机械能守恒，由ΔE减=ΔE增列出方程

【点评】该题目中很多学生错误地认为vA=vB，其实它们并不相等。由运动的合成与分解可知，球A在P点沿水平方向的运动是合运动，沿绳的运动是它的一个分运动，该分运动的速度大小与球B的速度大小相等。

【例3】如图4所示，滑块a、b的质量均为m，a套在固定直杆上，与光滑水平地面相距h，b放在地面上，a、b通过铰链用刚性轻杆连接。不计摩擦，a、b可视为质点，重力加速度大小为g。则

( )

A.a落地前轻杆对b一直做正功

C.a下落过程中，其加速度大小始终不大于g

D.a落地前，当a的机械能最小时，b对地面的压力大小为mg

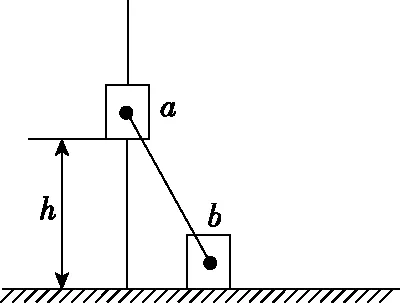
图4

图5

【答案】BD

(2)通过第(1)问的分析可知，b物体的速度先增大后减小，所以轻杆对b先做正功，后做负功，故A错误。

(3)因为a、b和杆组成的系统机械能守恒，所以a落地前当a的机械能最小时，b的机械能最大，速度最大，轻杆对它的作用力为0，故b对地面的压力大小为mg。当然轻杆对a的作用力也为0，所以a的加速度为g，C错误，D正确。

【点评】(1)该题是通过轻杆连接的系统，a沿杆竖直向下运动，b沿地面水平向右运动，两物体的速度不相等，但是它们沿杆的分速率是相等的，这是解决问题的关键。(2)当b物体的速度最大时，b的加速度为0，所受合力为0，则轻杆对b的作用力也为0，这是解答该题的又一个关键。

三、角速度相等的连接体模型

该模型的特点是两个物体通过刚性轻杆连接，因为它们在绕同轴转动的过程中在相等时间内转过的角度相等，所以这两个物体的角速度是相等的。这种模型中单个物体机械能也不守恒，但是系统的机械能守恒。

图6

【例4】如图6所示，长为2L的轻杆OB，O端装有转轴，B端固定一个质量为m的小球B，OB中点A固定一个质量为m的小球A，若OB杆从水平位置静止释放，则在它转到竖直位置的过程中，求：

(1)A、B球摆到最低点的速度大小分别是多少？

(2)轻杆对A、B球所做的功分别是多少？

(3)轻杆对A、B球做的总功是多少？

【错因分析】上述解法错误地认为轻杆对小球的作用力沿着杆的方向，对A、B两个小球不做功。事实上轻杆在向下摆动的过程中，轻杆对小球的弹力并没有沿着杆的方向，轻杆对小球是做了功的，所以A与地球组成的系统机械能不守恒，同样B与地球组成的系统机械能也不守恒。

【正解】(1)选A、B和地球为系统，系统中只有动能与重力势能发生了相互转化，故系统机械能守恒，则

又因为两小球的角速度相等

假设轻杆对A球做功为WA，由动能定理得

同理，假设轻杆对B球做功为WB，由动能定理得

(3)轻杆对A、B球所做的总功W=WA+WB=0。

【点评】该题轻杆对小球A做负功，对小球B做正功，轻杆对小球的作用力并没有沿杆的方向，轻杆的作用是实现A球与B球之间机械能的传递。

综上，用系统机械能守恒定律求解连接体问题时，其解题的策略有：

(1)选系统并判定系统的机械能是否守恒。

(2)选公式。机械能守恒定律常用的有三种表达式：①E1=E2(系统的初、末机械能相等)；②ΔEk=-ΔEp(系统动能的增量等于系统势能的减少量)；③ΔEA=-ΔEB(系统由两个物体组成时，A的机械能增量等于B的机械能减少量)。其中①式必须选择零势能参考平面，显得有些繁琐；②、③两式可不必选择零势能参考平面，且可统一成ΔE减=ΔE增，更显简洁、方便。