寓数于形 以形解数

陈太琼

摘  要：数学思想是数学的灵魂所在，也是解决数学问题的重要思路。数形结合作为一种应用非常广泛的数学思想方法，为学生认识抽象的数学知识提供了直观形象的材料。为此，教师应通过寓数于形、以形解数、数形结合的途径，充分结合“数”的准确性和“形”的直观性，引导学生更加全面地认识数学本质，拓宽学生的解题思维，提高学生的解题效率，促使学生数学学习效率的提升。

关键词：小学数学;数学思想;数形结合;教学策略

数形结合思想的本质是将复杂抽象的数量关系与简单直观的图形关系有机结合起来，通过充分挖掘题目中的已知条件和结论之间的隐含关系，利用数的精确化和形的直观化来研究数学问题，从而使得问题的求解变得更加简单直观。在小学数学教学中渗透数形结合思想方法，可以深刻地揭示数学的本质，启迪学生多角度、多层次地思考问题，有利于发展学生的思维能力，这对于培养学生数学思维和提高学生数学学习效率具有极为重要的理论与实践意义。

■一、寓数于形，帮助学生全面准确地理解知识

寓数于形是指利用精确的代数知识来解决比较抽象复杂的几何问题，引导学生通过画图等方式，从“数”的角度揭示“形”的规律，通过分析数量关系来判断几何图形的性质，更好地衬托出数学学科严密性与抽象性统一的本质特征。

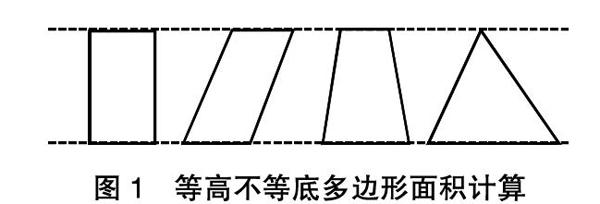
比如，在教学苏教版五年级上册“多边形面积的计算”这一内容时，笔者给出了这样一道习题：计算下面每个图形的面积（如图1），并对它们的面积进行对比，你能发现什么？

■

图1  等高不等底多边形面积计算

在教学过程中，笔者首先引导学生回忆三角形、长方形、梯形和平行四边形面积的计算公式，然后让学生利用直尺测量工具，对图1中四个图形的底边和高分别进行测量，由于这四个图形全部位于两条平行线之间，所以它们的高是相等的，只需要测量一次就可以了。到此，学生已开始从“形”逐渐向“数”的方向转变。经过测量，学生得到了图形的有关数据，再根据图形计算公式，就能轻易求出各个图形的面积。此时，学生对计算出的面积结果进行比较，未能从中发现什么，这是由于小学生的知识与经验缺乏所导致的，因此教师必须给予适当的引导。笔者带领学生再次回归题目——我们根据测量的数据，得出长方形、平行四边形、梯形和三角形的面积大小是相等的。也就是说，在等高的情况下：当面积相同时，三角形的底为平行四边形底的两倍;当长方形和平行四边形的底也相同时，他们的面积相同，长方形是一种内角为90度的特殊平行四边形;当梯形上下底边的和与三角形底边相等时，梯形的面积和三角形面积相等，而三角形是一种上底为0的特殊梯形。那么，面积相等的这四个图形，其周长大小是一样的吗？学生再次通过计算发现，面积相等的四个图形，其周长不一定会相等且周长由大到小的排序依次为平行四边形、长方形、三角形和梯形。笔者通过对这道例题的分析，不仅帮助学生回顾了图形面积和周长的计算公式，而且利用数的精准性，让学生更加深刻地掌握了图形的特征，有利于学生在原有认知基础上达到更深层次的认识。可见，寓数于形，能让学生从“数”的角度去体验图形的特征及转变，通过算一算、想一想的方式，引导学生发现其中蕴含的数学知识，体验数学学习的乐趣，让学生积极主动地投入数学学习中去。

■二、以形助数，帮助学生更好地理解抽象的数

“以形助数”是利用图形简单化和直观化的特点，帮助学生更好地理解抽象的数，从而更加轻松、便捷地求解题目。数学具有较强的抽象性，而小学生的思维仍然处于一种直观的形象思维中，运用数形结合思想，可以帮助他们顺利地从形象思想过渡到抽象思维，更好地理清数与形之间的关系，并能用图形的直观来研究有关数的问题。

比如在教学苏教版六年级上册“长方体和正方体体积”这一内容时，是从平面几何过渡到了立体几何。在教学中，我们发现学生虽然能对体积的计算公式熟记于心，但在对具体实物进行判断时却显得茫然而不知所措，出现这一现象的根源在于学生未能将体积的数的概念与实物大小之间的关系对应起来。为了有效解决上述问题，笔者首先利用乌鸦喝水的故事创设教学情境，帮助学生建立体积的表象，并逐渐从立方厘米、立方分米到立方米进行螺旋式上升，为学生初次学习有关体积知识奠定基础;然后让学生分组利用课前准备好的小正方体物品，摆出任意大小的长方体，分别测量它的长、宽和高，并思考自己的长方体一共用了多少个小正方体？如何计算该长方体的体积？小正方体和长方体之间有什么关系呢？学生通过观察对比、动手实践等多种方式，逐渐将体积单位与实物大小之间的关系对应起来，这样就利用直观化的形更好地帮助学生理解了体积公式中数的内涵。

■三、数形结合，提高学生解决问题的能力

数形结合是指在求解数学问题时综合利用寓数于形和以形助数的思想方法，即同时从“数”和“形”入手，通过分析已知条件和结论，寻找“数”与“形”之间的内在联系，以此达到高效率解决数学问题的目的，从而促进学生解题能力的提升。

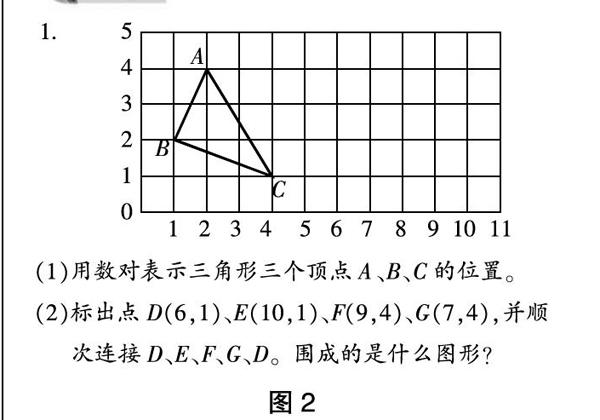
比如在教学苏教版五年级下册“确定位置”这一内容时，由于学生在一年级和二年级已经学习过“位置认识”的相关知识，加之学生在日常生活中也经历了很多隐含数对的知识与经验，于是笔者在本节课的教学中结合课后习题中的练一练（如图2），为学生提供了探究的机会，引导学生通过对比、分析、思考与交流的過程，学会用数对的方法来确定位置，有效培养了学生的空间观念。

在教学过程中，笔者首先引导学生在方格纸中寻找三角形三个顶点A、B和C的位置，并尝试利用数对的形式进行表达。同时，为了避免学生在找位置的过程中出现串行的问题，笔者强调要利用三角尺来寻找位置，这样既提高了寻找速度也避免了错误。为了更好地帮助学生理解数对与图形之间的关系，笔者继续让学生将三角形ABC向上、下、左、右任一方向平移3个单位，操作发现：在平移的过程中，三角形的图形没有任何变化，变化的只有顶点位置的数对。这样用数对来表示位置的方法，巧妙地将数与形结合在一起，通过平移操作让学生更加清晰地认识到：数对的变化只能引起图形位置的变化，而对图形的大小及形状没有任何影响，这也说明了数对与方格上的点是一一对应的关系。

■四、结语

综上所述，小学数学是培养逻辑思维的重要课程。生活化数学概念及数学的抽象性使得数形结合思想在教学中的应用更加广泛，这不仅使数学知识更利于学生理解与掌握，而且能让学生体会到数学学习的快乐和有趣并整理出一套逻辑清晰且合理的数学学习方法，大大拓宽了学生的解题思路，也为学生学习更高层次的数学知识奠定了方法基础。