探讨函数零点在导数不等式中的应用
——“隐零点(虚拟零点)”与“小不等式”的巅峰对决
四川
函数零点是沟通函数、方程、不等式的重要载体,其充分体现了数学核心素养,体现了函数与方程、数形结合、转化与化归思想在中学数学中的应用,从近几年高考试题来看,函数零点问题备受青睐,特别是在研究函数与导数零点存在,但又不能求出零点的具体值时,常根据二分法思想找出零点的大致范围,再借助零点范围及其等量关系,解决不等关系或参数范围问题,从而由考查函数零点的知识性逐步向工具性转变,这也体现新课标精神由知识立意向能力立意转变,本文与大家一起探讨函数“隐零点(虚拟零点)”为载体艺术与“小不等式”过渡转化在导数不等式中的应用.
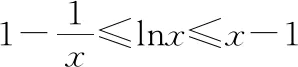
类型一:以“隐零点(虚拟零点)”为载体过渡对决“小不等式”证明不等关系
例1.已知函数f(x)=ex-ln(x+m).
(Ⅰ)设x=0是f(x)的极值点,求函数f(x)在[1,2]上的最值.
(Ⅱ)当m≤2时,证明f(x)>0.
试题分析:问题(Ⅰ)根据函数极值点处导数的函数值为零建立等量关系,求出参数的值;再判断f(x)在[1,2]上的单调性,从而求出f(x)的最值.
问题(Ⅱ)当m≤2时,要证f(x)>0.即证ex-ln(x+m)>0,
思路1:因ln(x+m)≤ln(x+2),放缩即证当m=2时f(x)>0即可;
思路2:直接证明,二次求导,利用讨论的思想证明其最小值大于零;
思路3:利用小不等式ex≥x+1放缩证明.
试题解析:(Ⅰ)最大值e2-ln3,最小值e-ln2.



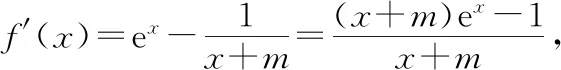
设g(x)=(x+m)ex-1,而g′(x)=(x+m+1)ex>0,所以g(x)在(-m,+∞)上单调递增,当x→-m时,g(x)→-1,当x→+∞时,g(x)→+∞,必存在一个数x0,使得g(x0)=0,则当x∈(-m,x0)时,g(x)<0,f′(x)<0,f(x)单调递减;
当x∈(x0,+∞)时,g(x)>0,f′(x)>0,f(x)单调递增;故f(x)min=f(x0),


综上,当m≤2时,f(x)>0.
解法3:对x∈R时,设k(x)=ex-x-1,则k′(x)=ex-1,令k′(x)=0得x=0.
当x∈(-∞,0)时,k′(x)<0,k(x)单调递减;
当x∈(0,+∞)时,k′(x)>0,k(x)单调递增.
故k(x)min=k(0)=0,即k(x)=ex-x-1≥0得ex≥x+1(当且仅当x=0时取等号).
当m≤2时,要证f(x)>0,即证x+1>ln(x+m).

当x∈(1-m,+∞)时,h′(x)>0,h(x)单调递增.
故h(x)min=h(1-m)=2-m≥0.因为前后不等式不能同时取到等号,
所以当m≤2时,f(x)>0.
评析:此题第(Ⅱ)问解法1充分利用参变量的放缩,大大减小计算量,但解法1、2本质都是先运用零点存在性定理确定导函数有零点,并对其零点设而不求,然后采取整体代换的策略,把最值表达式中的超越式转化为普通代数式,构造关于零点的函数,结合零点的范围,利用函数单调性,基本不等式,放缩等手段求最值达到证明不等式.解法3,先利用ex≥x+1把超越不等式放缩成普通的代数不等式,再构造函数证明不等关系.三种方法的共性都是想办法把超越不等式转化为普通不等式,再构造新函数解决问题.
变式训练1:已知函数f(x)=x2-(a-2)x-alnx(a∈R).
(Ⅰ)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求函数y=f(x)的单调区间;
(Ⅲ)当a=1时,证明:对任意的x>0,f(x)+ex>x2+x+2.
试题解析:(Ⅰ)2x+y-2=0.
(Ⅱ)当a≤0时,f(x)的单调递增区间为(0,+∞);



当x∈(0,x0)时,h′(x)<0,函数h(x)单调递减;
当x∈(x0,+∞)时,h′(x)>0,函数h(x)单调递增;

即ex-lnx-2>0在(0,+∞)上恒成立,
所以对任意x>0,f(x)+ex>x2+x+2恒成立.
解法2:对x∈R时,设k(x)=ex-x-1,则k′(x)=ex-1,令k′(x)=0得x=0,当x∈(-∞,0)时,k′(x)<0,k(x)单调递减;当x∈(0,+∞)时,k′(x)>0,k(x)单调递增;故k(x)min=k(0)=0,即k(x)=ex-x-1≥0得ex≥x+1(当且仅当x=0时取等号),

当x∈(0,1)时,h′(x)<0,h(x)单调递减;
当x∈(1,+∞)时,h′(x)>0,h(x)单调递增;
故h(x)min=h(1)=0,即h(x)=x-1-lnx≥0得lnx≤x-1(当且仅当x=1时取等号).
当a=1时,要证不等式f(x)+ex>x2+x+2可变为ex-lnx-2>0,由ex≥x+1与lnx≤x-1即证x+1-(x-1)-2≥0恒成立,由于不能同时取到等号,故对任意的x>0,f(x)+ex>x2+x+2.
类型二:以“隐零点(虚拟零点)”为载体过渡求解参数的最小(大)整数问题
例2.已知函数f(x)=(x-1)ln(x-1).
(Ⅰ)设函数g(x)=-a(x-1)+f(x)在区间[2,e2+1]上不单调,求实数a的取值范围;
(Ⅱ)若k∈Z,且f(x)+x-1-k(x-2)>0对x>2恒成立,求k的最大值.
试题分析:问题(Ⅰ)转化为g′(x)=0在[2,e2+1]有零点.
问题(Ⅱ)当x>2时,采用分参思想,构建新函数,转化为求解函数的最值问题,在通过隐零点过渡找到最值的范围,从而确定所求整数的最值.
试题解析:(Ⅰ)a的取值范围为(1,3).
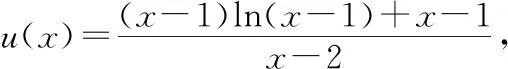


因为x>2,所以v′(x)>0,即v(x)在(2,+∞)上单调递增.
又因为v(4)=-ln3+1<0,v(5)=-2ln2+2>0.
所以∃x0∈(4,5),使得v(x0)=0即u′(x0)=0,所以u(x)在(4,x0)上递减,在(x0,5)上递增.
所以u(x)min=u(x0)
=x0-1∈(3,4).
k 评析:此题第(Ⅱ)问通过分参构造第一个函数,求导寻找最值,借助隐零点过渡构造第二个函数,结合隐零点的范围,确定第二个函数的值域,从而确定整参变数的最值. 变式训练2:已知函数f(x)=xlnx+ax+b在点(1,f(1))处的切线为3x-y-2=0. (Ⅰ)求函数f(x)的解析式; 试题解析:(Ⅰ)f(x)=xlnx+2x-1. 所以h(x)在(0,+∞)上为增函数.又h(2)=1-ln3<0,h(3)=2-ln4>0, 故存在唯一的x0∈(2,3)使得h(x0)=0,即x0-1=ln(x0+1). 当x∈(0,x0)时,h(x)<0, 所以g′(x)<0,所以g(x)在(0,x0)上为减函数; 当x∈(x0,+∞)时,h(x)>0, 所以g′(x)>0,所以g(x)在(x0,+∞)上为增函数. 所以k>x0+2.因为x0∈(2,3),所以x0+2∈(4,5).因为k∈Z,所以k的最小值为5. (Ⅰ)当a<0时,讨论函数f(x)的单调性; 试题分析:问题(Ⅰ)在函数定义域(0,+∞)上求导,再通过因式分解讨论单调性. 思路3:利用不等式ex≥x+1在x=0时取等号,求得实数b的取值范围. 试题解析:(Ⅰ)函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减. (Ⅱ)解法1:利用“隐零点(虚拟零点)”为载体过渡构建k(x)=xlnx. g(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,g(x)min=g(x0), 解法2:利用“隐零点(虚拟零点)”为载体过渡构建k(x)=xex. g(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,g(x)min=g(x0), 解法3:利用不等式ex≥x+1在x=0时取等号求解.



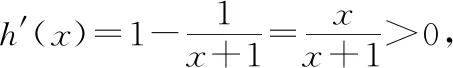
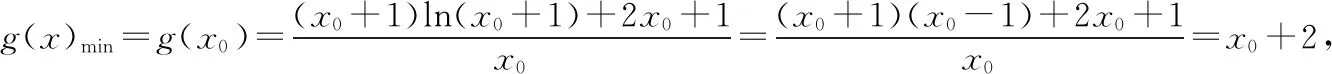
类型三:以“隐零点(虚拟零点)”为载体过渡对决“小不等式”求参数的范围