高考全国卷立体几何“球”的考查特点和备考策略

广东

随着课程改革实施的推进，“新课程标准(2017版)”逐渐为一线教师所熟悉，与“旧课程标准(2013版)”相比，不论是课程体系的设置，还是具体的内容要求，都发生了不同程度的变化.其中，与空间几何体相关的内容要求发生了较大的变化，主要体现在三个方面：第一，删除了三视图，以及与三视图有关的平行投影和中心投影；第二，提高了关于球、棱柱、棱锥、棱台表面积和体积公式的要求，行为动词从“了解”调整为“知道”和“能用”；第三，提高了关于简单空间图形的要求，从“简易组合”调整为“简单组合”.课程标准的变化在2018年的高考试题中也有所体现，未出现与三视图有关的试题，因此，高考备考有必要研究三视图以外的其他题型，本文对历年全国卷与球有关的试题进行了深入的分析，与读者分享.

1.历年全国卷高考“球”的试题考点统计

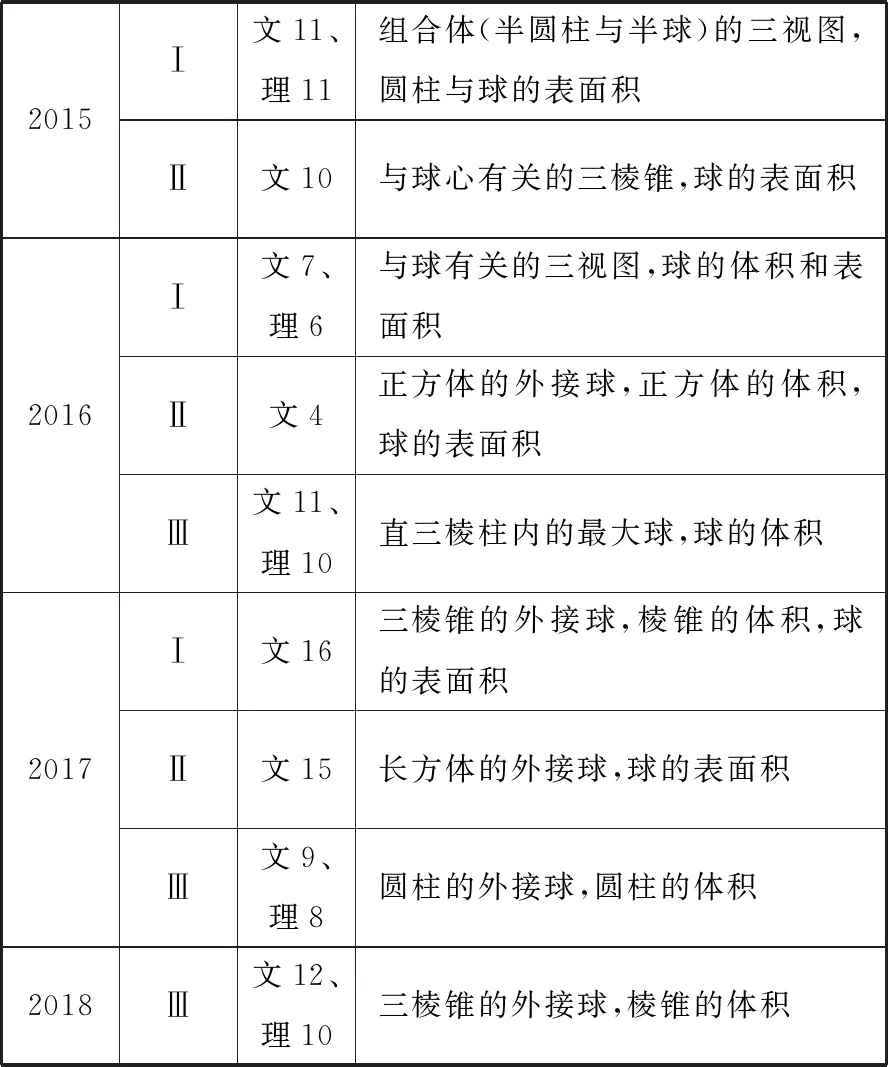
续表

通过对历年全国卷高考试题的研究，不难发现与“球”有关的考题极具规律，重在考查常见几何体与球组成的简单图形，以及常见几何体的表面积和体积.下面结合2019年高考考试说明和全国卷高考试题具体分析“球”的考查内容、方式，以及备考策略.

2.全国卷高考“球”的考查特点及备考策略

2019版《普通高等学校招生全国统一考试大纲说明》(文、理相同)中与“球”有关的描述主要有“认识柱、锥、台、球及其简单组合体的结构特征”“能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述三视图所表示的立体模型，会用斜二测法画出它们的直观图”“了解球、棱柱、棱锥、棱台的表面积和体积的计算公式”.通过考试说明来看，高考对“球”的考查内容和形式与以往保持一致，依然会体现在对“球的结构特征”“识图、画图”“表面积和体积公式”等方面的考查.

2.1突出对简单几何体外接球的考查

例1.(2017·全国卷Ⅲ理·8)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为

( )

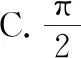
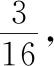
【备考策略】对简单几何体外接球的考查，多以长方体、正棱柱、正棱锥、圆柱、圆锥为考查核心，复习备考时可将几何体分为柱体、锥体两大类.对于长方体、正棱柱等柱体，可以利用圆柱作为载体来研究其外接球的问题，研究方法类似于例1；对于正棱锥等锥体，可以利用圆锥作为载体来研究其外接球的问题，研究方法类似于例2.反之，也可以利用圆柱的内接柱体、圆锥的内接锥体来设计一些几何体的外接球问题，合理拓宽备考路径.

2.2强调对球的几何性质的考查

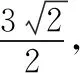
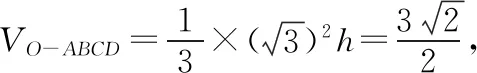
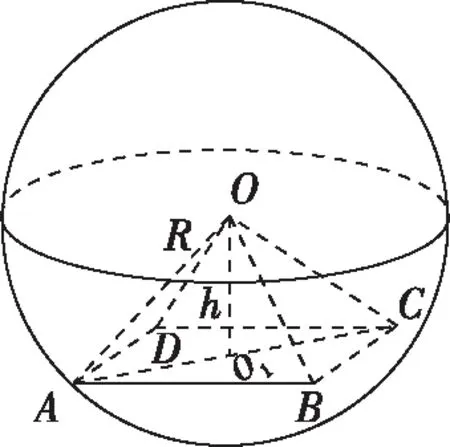
【备考策略】对球的几何性质的考查，以性质R2=r2+d2为考查核心，其中R为球的半径，r为小圆的半径，d为小圆圆心到球心的距离.复习备考时，可从两个角度对例3进行变式设计，角度一：将球内正四棱锥替换成其他常见几何体(如三棱锥等)或平面图形，如截面圆(2013年卷Ⅰ文15、2012年文8)、矩形(2011年理15)等；角度二：将球内几何体替换成球外几何体，如将球放置于正方体上(2013年卷Ⅰ理6)等.不论几何图形如何变化，都可以通过培养学生利用截面的眼光寻找几何图形中的直角三角形，来强化球的几何性质的应用.

2.3注重对与球有关的几何图形画图能力的考查

例4.(2017·全国卷Ⅰ文·16)已知三棱锥S-ABC的所有顶点都在球O的球面上，SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9，则球O的表面积为________.

( )

【备考策略】上述两道试题的难点集中体现在几何图形的画图能力上，充分体现了几何直观素养的命题导向.其中，例4体现了静态的几何图形，画图时需要引导学生选择恰当的图形(平面SAC或平面SBC)作为底面，例5体现了动态的几何图形，画图时需要引导学生选择相对静态的图形(平面ABC)作为底面，不论哪种几何图形，在画底面的直观图形时，都需要引导学生画好水平基线.总之，球的复习备考要关注几何图形的画法教学，培养学生的画图能力.

2.4指向与球有关的三视图识图能力的考查

( )

A.17π B.18π

C.20π D.28π

2.5着眼于几何体内最大球的考查

例7.(2016·全国卷Ⅲ理·10)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC，AB=6，BC=8，AA1=3，则V的最大值是

( )

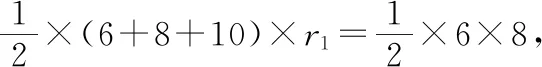
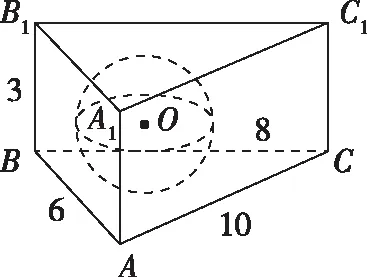
【备考策略】与几何体的外接球相比，全国卷很少考查几何体的内切球，例7的考查与内切球有一定的联系，但是能力要求较高.作为新兴题型，复习备考可以考虑从常见几何体的内切球问题开始，掌握轴截面法和等体积法等基本方法，再复习几何体内的最大球问题，强化分类讨论的思想方法，以及平面化的研究方法，从水平轴截面和竖直轴截面两个维度求解几何体内最大球的半径，突破新兴题型.

3.一点感想