螺旋槽旋转密封瞬态启停工况动态特性分析
(北京航天发射技术研究所 北京 100076)
在车辆传动领域,旋转密封是一种特殊形式的端面动密封,广泛应用于传动系统的液控旋转机构中,如液力变矩器、湿式离合器、制动器等。在这些机构中,旋转密封保证压力油从静止件流入旋转轴进行动力传递,并维持系统油压,因此它是保证整个传动系统正常工作的重要环节,其一旦失效将导致整个传动系统的故障[1]。
表面微槽型旋转密封由于其良好的流体动压效应,能够改善摩擦面的润滑状态,达到流体动力润滑状态[2]。目前,针对微槽型旋转密封的文献往往立足于工况参数一定的稳态特性[2-3]。然而,旋转密封工作条件复杂多变,并往往伴随有外界冲击,尤其是启停工况下转速的突变。显然在启停过程中油膜的挤压效应具有显著影响,忽略挤压效应对旋转密封性能的分析将产生较大的误差。
在端面密封、推力轴承领域,多数学者采用摄动法分析其动态特性参数[4-6]。然而,该方法无法获得关键的润滑特性参数,如泄漏量、摩擦转矩与粗糙峰承载力。GREEN等[7-8]在气体机械密封动力学方面做出了突出的贡献,研究了静环偏心、动环径向跳动及动态稳定性等问题。目前,对于旋转密封还没有文献结合实际工作状态建立其动力学模型,并进行动态响应分析。因此,本文作者耦合动力学、润滑力学与接触力学,结合实际工作状态建立了螺旋槽旋转密封的摩擦动力学模型,分析启停工况下旋转密封的动态特性。
1 摩擦动力学模型与计算方法
1.1 动力学模型
在车辆传动系统中,旋转密封典型的应用形式如图1所示,其作用为密封旋转轴和配油衬套之间的压力油。在油液压力和自身弹力的作用下,密封环端面与旋转轴内侧壁相接触形成动密封面A,密封环外圆面与配油衬套内环壁相贴紧形成静密封面B,螺旋槽位于密封面A上。由于密封面A与对偶面的相对旋转运动且有较大的压紧力,将产生强烈的摩擦磨损。因此为提高密封环工作可靠性,需对密封面A润滑状态进行重点研究。图1示出了密封环在x轴方向上的受力情况,可表达为
(1)


图1 旋转密封工作原理图
1.2 流体润滑模型
图2所示为旋转密封的螺旋槽结构示意图。ri和ro分别为密封环内外径,rg为螺旋槽外圆半径,pi和po分别为内外径压力,h0为液膜厚度最小值,hg为螺旋槽槽深,在非槽区液膜厚度为h0,在槽区液膜厚度为h0+hg,θl和θg分别为台区和槽区对应的角度,β为螺旋角,Ng为槽数。定义量纲一化参数周向槽台比δθ=θg/(θg+θl)、 径向槽台比δr=(rg-ri)/(ro-ri)。
液压油是旋转密封润滑介质。考虑挤压效应,等温条件下理想液体柱坐标雷诺方程[9]可以描述为
(2)
式中:r为径向坐标;θ为圆周坐标;p为油膜压力;ω为密封副相对旋转角速度;ρ为油液密度;μ为油液动力黏度;h为油膜厚度;t为时间。

图2 螺旋槽结构示意图
在实际工作过程中,端面液膜可能产生空化现象。为了提高计算效率,文中采用Reynolds边界条件。由于密封环的中心对称性,计算时选取一个计算周期(即一个槽区和相邻的两个半台区)。因此,式(2)的积分边界条件为
(3)
其中,θ0=2π/Ng。
螺旋槽的存在给式(2)的求解带来了困难,文中采用贴体坐标变换[10]的方法生成计算网格,这样网格边界与槽台、槽坝边界相重合,实现一个计算单元内的膜厚的一致。采用有限体积法[2]对式(2)进行离散,应用Gauss-Seidel松弛迭代方法求解密封端面压力分布。迭代计算收敛后,在计算区域积分可以得到螺旋槽旋转密封性能参数:
流体的承载力
(4)
流体摩擦转矩
(5)
流体泄漏量
(6)
1.3 粗糙峰接触模型
粗糙峰接触特性采用统计接触模型进行描述。根据CHANG等[11]的接触模型,粗糙峰承载力可以表示为
Fas=Fe+Fp
(7)
其中,Fe和Fp分别表示粗糙峰弹性与塑性变形条件下的承载力,计算公式如下
(8)
(9)

基于JACKSON和GREEN微凸体弹塑性接触理论[12],划分弹性与塑性接触状态的临界变形量可表示为
(10)
粗糙峰表面形貌特征可以由三个特征参数描述:粗糙峰点密度η、粗糙峰综合粗糙度σ与微凸体平均曲率半径R[13]。这三个特征参数可以根据表面粗糙峰分布信息计算获得。
1.4 外圆面摩擦力
根据密封环运动状态,外圆面摩擦力可分为滑动摩擦力与静摩擦力。文中假设外圆面最大静摩擦力与滑动摩擦力相同。作用于外圆面的载荷Fr由密封环油液压力与自身弹性恢复力两部分组成,可表达为
(11)
式中:pk为单位面积密封环弹力;L为密封环宽度。
假设外圆面滑动摩擦因数为fcf,则最大静摩擦力Ff_max=fcf·Fr。因此,瞬态启停工况下静摩擦力由下式给出
Ff_st=-sign(Fld+Ffl+Fas)·min(Ff_max,abs(Fld+Ffl+Fas))
(12)
式中:sign()为符号函数。
同样地,滑动摩擦力如下
(13)
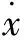
1.5 计算方法
由于流体与粗糙峰承载力强烈的非线性及相互耦合特性,式(1)的求解常采用线性多步法,例如NDF与BDF算法[14]。文中采用可变阶数同时自动调整步长的NDF算法[15]对式(1)进行求解,获得瞬态启停工况下密封环动态响应规律。
2 模型验证
文中计算结果与QIU和KHONSARI[16]的试验结果对比如图3所示。可以看出,计算结果与试验结果匹配得很好。但是,当转速大于300 r/min时,计算结果稍大于试验结果,这可能是因为计算选取的油液温度为油池温度,该温度小于实际试验中摩擦副的温度,导致计算时油液黏度较大,从而使计算得到的摩擦因数较大。

图3 计算结果与试验结果对比
3 结果与讨论
以典型螺旋槽旋转密封为例进行分析,其结构和工况参数如表1所示。特别地,采用触针式表面形貌测量仪对密封面进行分析,计算得到粗糙表面的粗糙峰综合粗糙度σ,粗糙峰点密度η与微凸体平均曲率半径R。为了反映密封环瞬态启停工况下的极限工作能力,文中分析工况为转速阶跃响应,转速变化情况如图4所示,在t=0.01 s转速从1 000 r/min分别阶跃到2 000、3 000、4 000、5 000 r/min,在t=0.02 s又阶跃下降到1 000 r/min。

表1 螺旋槽旋转密封结构与工况参数

图4 转速阶跃变化
按照表1进行计算,螺旋槽旋转密封在瞬态启停工况下的动态特性如图5所示。
由图5(a)可知:在t=0.01 s,随着转速阶跃升高,流体动压效应瞬间增强,相应地流体承载力阶跃增大(如图5(c)所示),因而最小油膜厚度逐渐升高;在之后的0.005 s之内,最小油膜厚度趋于稳定。相同地,对于4 000和5 000 r/min,在转速阶跃下降的t=0.02 s,膜厚逐渐下降并在0.005 s内恢复稳定;而对于转速阶跃下降的2 000和3 000 r/min,膜厚保持不变。膜厚变化规律不同的原因是外圆面摩擦力特性导致的。转速从4 000和5 000 r/min阶跃下降到1 000 r/min后,主动力的合力大于最大静摩擦力;而转速从2 000和3 000 r/min阶跃下降到1 000 r/min后,主动力的合力小于最大静摩擦力,所以此时密封环继续保持稳定工作状态,膜厚保持不变。总的来说,转速越高带来更强的流体动压效应,密封环摩擦面膜厚越大。
同样地,密封环速度的波动也是由于流体动压效应。由图5(b)可知:在t=0.01 s,转速的提高使流体承载力增大,密封环速度迅速升高,膜厚变大,但膜厚与速度的增大有减小流体承载力的作用,所以之后密封环速度逐渐减小,并在0.005 s内趋近于0;在t=0.02 s,由于转速的阶跃变化带来密封环速度的阶跃变化,密封环速度首先向x轴负方向阶跃增大到一定值,随后逐渐趋于0,使得挤压效应成为影响流体润滑特性的主要因素。对于不同幅值的转速阶跃变化,转速阶跃幅值变化越大,对密封环瞬态平衡影响越大,因而密封环速度波动越大。转速阶跃增大与阶跃减小时,密封环速度变化不对称,这是由于密封环外圆摩擦力的存在。在转速阶跃下降时,外圆摩擦力方向由x轴负方向变化为x轴正方向,外圆摩擦力方向变化带来其阶跃变化,阻止密封环沿x轴负方向速度的增大,严重削弱挤压效应,有效保护密封环膜厚的减小,阻止密封环向混合摩擦状态进一步发展,有利于保持密封环的流体润滑状态,减小摩擦磨损。
由图5(c)可知:在t=0.01 s,转速的阶跃升高,流体承载力的阶跃增大,但同时快速升高的密封环速度有很强的反挤压效应,因而转速阶跃变化后流体承载力快速下降;与之相反,在t=0.02 s,沿x轴负方向增大的密封环速度有很强的挤压效应,所以流体承载力阶跃减小后快速升高;在转速稳定状态时,即密封环速度较小时,此时流体动压效应重新成为主导因素,油膜厚度是影响流体承载力的主要因素。
与流体承载力不同,粗糙峰承载力是固体的接触,其与密封环的接触程度即膜厚直接相关,与流体动压效应不直接相关。所以,粗糙峰承载力随膜厚的增大而减小,随膜厚的减小而增大,其不会阶跃地增大或减小。由图5(d)可知:转速从1 000 r/min阶跃升高到5 000 r/min后,粗糙峰承载力变为0,说明此时膜厚提高到较大值,旋转密封从混合润滑状态进入完全的流体动力润滑状态。特别地,密封环在启动之前和停机之后,虽然外界工作状态参数一样,但粗糙峰承载力并不相同,这是由于膜厚的不同。停机之后较启动之前油膜膜厚变大,粗糙峰接触程度降低,粗糙峰承载力下降,因此停机之后旋转密封有更好的润滑条件。
如图5(e)所示,转速与膜厚对流体摩擦转矩的影响最大。因此,启动与停机瞬时,转速越高,流体摩擦转矩越大;转速稳定后,流体摩擦转矩与膜厚反相关。
流体泄漏量主要受挤压效应、膜厚与转速的影响,它的变化规律与流体承载力的类似。在启动时,密封环速度的极剧增大,反挤压效应大大增强,流体泄漏量变为负值(如图5(f)所示),说明此时旋转密封出现回流现象。在停机工况,情况相反,挤压效应使流体泄漏量增大。

图5 瞬态启停工况动态特性参数变化规律
4 结论
(1)在启停工况中,螺旋槽旋转密封有稳定且快速的阶跃响应,其能够在0.005 s内恢复到稳定工作状态。
(2)在启动和停机时,首先是流体动压效应主导螺旋槽旋转密封的润滑状态,之后挤压效应成为主要作用因素,然后流体动压效应重新成为主导因素。
(3)启停工作过程中,对于特定结构参数的螺旋槽旋转密封,设计合适的外圆面摩擦力有利于保持较大的膜厚,减小粗糙峰接触程度,改善润滑条件。

