往复密封数值仿真模型及试验验证*
黄 兴 夏迎松2 黄 乐 郭 飞3 贾晓红3 王文虎
(1.广州机械科学研究院有限公司 广东广州 510700;2.安徽中鼎密封件股份有限公司 安徽宣城 242300;3.清华大学摩擦学国家重点实验室 北京 100084)
橡塑密封是工业设备的关键、核心基础零部件之一,是设备安全可靠运行的重要保障。而往复密封又是一种常用橡塑密封形式,开展其性能研究,研制高性能往复密封对加快我国工业强国的进程具有重要意义。
往复密封的研究起始于20世纪30年代,直到最近十几年随着计算机的普及和数值方法的完善,往复密封的数值研究才得以发展[1]。近些年不少学者基于有限元方法开展了往复密封力学性能和结构分析[2-4]。但通过有限元分析方法只能获得密封圈的应力应变状态,通过这些信息只能间接判断密封圈的性能优劣,这是由于有限元分析只能对密封圈的受力变形进行求解,未能考虑润滑介质的影响,无法得到可直接表征密封圈性能的摩擦力、泄漏量等参数的大小。
因此,本文作者基于混合润滑建立往复密封数值仿真模型,实现密封性能参数如摩擦力、泄漏量的仿真计算,并通过往复密封基础试验台开展斯特封台架试验,验证模型计算结果的正确性,从而为往复密封的设计评价提供参考。
1 往复密封系统及仿真模型
图1给出了一种斯特封往复密封系统。斯特封处于压缩状态安装在缸筒沟槽上,其单向密封的作用,斯特封压缩量的大小由斯特封及其安装沟槽的内外径尺寸共同决定。工作时,轴在外力的驱动下做往复运动,斯特封的图示右侧会承受介质压力。
稳态下,斯特封的密封接触区存在3个力,分别是斯特封弹性变形产生静态接触压力psc、流体动压产生的油膜压力pc以及粗糙峰接触产出的粗糙峰接触压力pcon。其中,油膜压力与粗糙峰接触压力之和与静态接触压力的大小相等[5]。

图1 斯特封的往复密封系统示意图
1.1 计算流程
数值仿真流程就是通过修正油膜厚度使上述这3个力达到平衡状态,求解过程如图2所示。
首先,通过有限元分析软件ANSYS对密封件进行固体力学分析求解密封件的静态接触压力psc和影响系数矩阵In,然后假定初始膜厚分别通过流体力学分析、接触力学分析求解油膜压力pc、粗糙峰接触压力pcon,再通过变形力学分析基于影响系数法确定油膜厚度的修正量,反复迭代最终达到的三力平衡状态,获得此时的接触区的油膜厚度、油膜压力、粗糙峰接触压力等信息,进而求出密封件泄漏量和摩擦力等性能参数。

图2 数值仿真流程图
1.2 固体力学分析
通过有限元分析方法模拟密封件的受力变形,获得密封圈的静态接触压力和影响系数矩阵。由于斯特封的结构和受力具有轴对称特点,为了提高计算速度,节省计算机资源,分析采用了2D轴对称模型[6];选用高阶单元PLANE183作为分析单元;选用Mooney-Rivlin模型作为密封件弹性体的材料本构模型,通过标准的单轴拉伸压缩实验获得材料的应力应变关系,再由ANSYS软件拟合得到Mooney-Rivlin模型中的材料参数;选用四边形网格对模型进行网格划分[7](如图3所示)。

图3 网格划分
通过四大载荷步进行有限元分析,第一个载荷步是模拟斯特封的O形圈与耐磨环的过盈配合,第二个载荷步是通过对活塞或缸筒施加X方向的位移载荷模拟斯特封的预紧装配状态,第三大载荷步是通过对斯特封施加均布压力模拟其承压工作状态,均布压力的施加边界通过循环迭代的方法获取,第四大荷步则是用于计算斯特封接触区的影响系数矩阵In。
1.3 流体数值计算
油膜稳定状态下密封性能参数通过求解一维雷诺方程获得,方程中引入空化指数F和通用变量Φ来表征空化效应,同时基于统计学采用流量因子描述唇口粗糙度对流场的影响,密封接触区的粗糙峰接触力利用Greenwood-Williamson接触模型进行计算,变形分析中通过利用影响系数法得到密封件接触区的法向变形[8-10]。
2 试验台架
通过往复密封基础试验台架开展斯特封密封特性的试验研究,来验证数值仿真模型的正确性。往复密封实验台的基本结构示意图如图4所示,包括高低温箱、被试缸、驱动缸、支撑平台、拉压力传感器、泄漏量测量系统、位移传感系统、温度传感器等。其中高低温箱具有制冷和加热功能,可实现-45~120 ℃范围内的温度变化,且底部装有滚轮,可以视实际需要配合被试缸开展往复密封件的高低温试验。被试缸与驱动缸之间装有拉压力传感器,通过传感器测量往复运动过程中密封圈的摩擦力。

图4 往复基础试验台示意图
被试缸的结构如图5所示,缸中有2个密封槽块,用以安装被试密封件,拉压传感器测得的就是被试缸中2个密封圈的摩擦力合力,单个斯特封的摩擦力近似等于测量值的1/2。
图5 被试缸结构示意图
由于正常安装的斯特封在工作中是零泄漏的,因此试验时将其进行反装,使其发生泄漏,从而实现其泄漏量测量。
3 计算结果及分析
选择规格为φ36 mm×φ46.7 mm×4.2 mm斯特封开展台架试验,斯特封耐磨环的材料为PTFE,O形圈的材料为NBR,分析其在不同介质压力、不同速度下正反装的摩擦力与泄漏量,并通过试验台架验证计算结果的正确性。相关参数如下:NBR材料Mooney-Rivlin模型参数C10=0.88 MPa,C01=2.27 MPa,C11=4.01 MPa,PTFE材料的弹性模量E=900 MPa,泊松比ν=0.4,摩擦因数f=0.1。内外行程压力pf=0.1~35 MPa,环境压力pa=0.1 MPa,空化压力pcav=0,往复速度v=0.05~0.5 m/s,行程长度B=0.4 m,缸径Di=36 mm,润滑油黏度μ=0.04 Pa·s。
通过美国zygo公司的Zegage形貌测量仪测量斯特封的表面粗糙度,测量结果如图6所示,通过多次测量取平均值得出斯特封密封面的方均根粗糙度值σ=4.5 μm。

图6 斯特封耐磨环表面形貌测量结果
在速度0.3 m/s,介质压力0.1~35 MPa下测量斯特封的摩擦力。摩擦力仿真结果与试验结果对比情况如图7所示。可以看出:不同介质压力下的仿真结果与试验测量结果都比较接近,变化趋势也比较吻合,说明数值模型的计算结果有较高的参考价值。
在速度0.5 m/s,介质压力35 MPa下对斯特封进行了试验,测量了反装斯特封往复运动10万次过程中的泄漏量,并对比反装斯特封泄漏量的仿真计算结果,对比情况如图8所示。可以看出:试验与仿真结果比较接近,变化趋势非常吻合,说明数值模型的泄漏量的计算结果有较好的参考价值和可信度,由于仿真计算未考虑斯特封往复运动过程中的磨损现象,使得试验后期测得的泄漏量比仿真计算结果偏大。

图7 摩擦力随压力变化对比结果
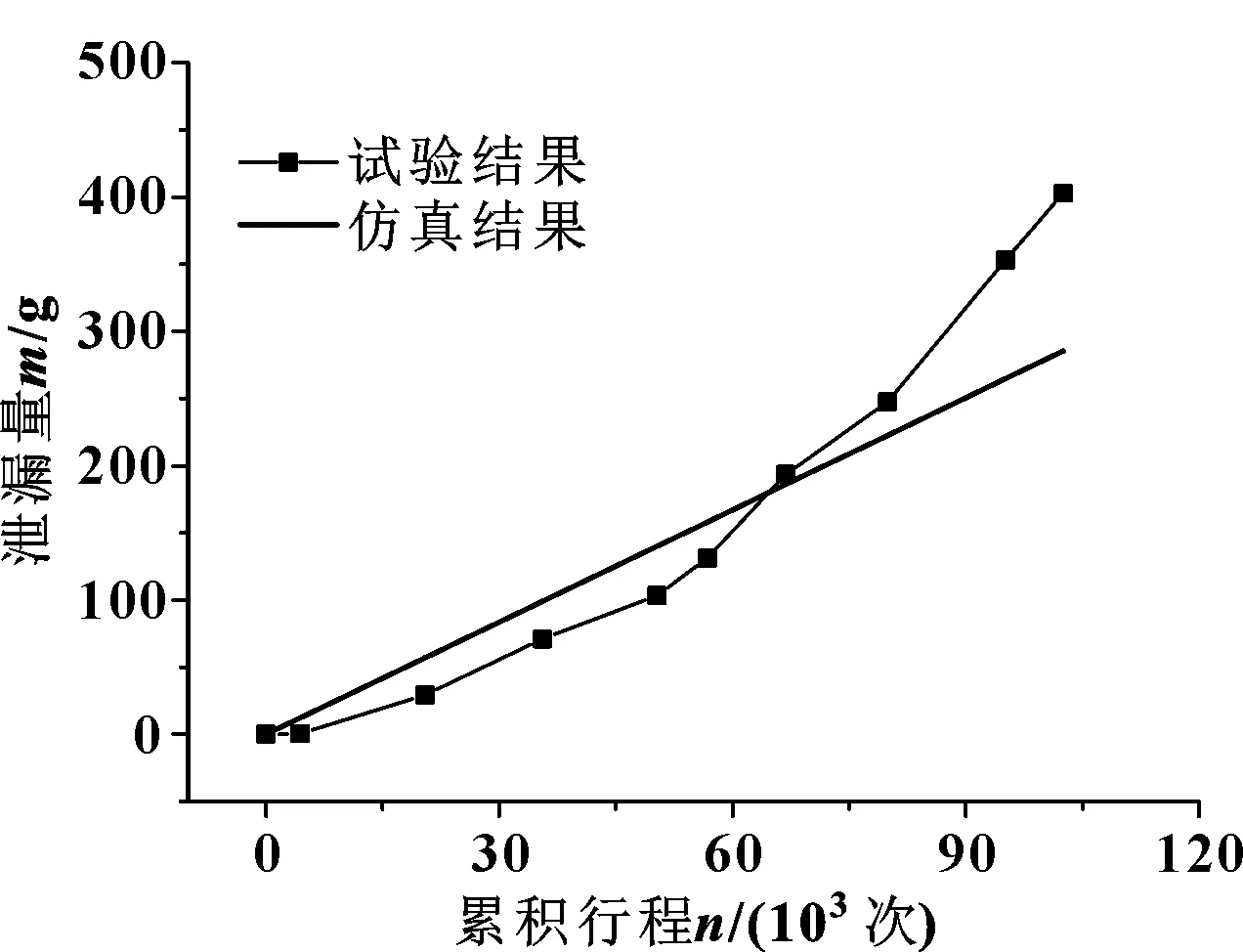
图8 泄漏量测量与仿真结果对比
4 结论
(1)综合考虑密封系统的固体力学分析、流体力学分析、接触力学分析以及变形力学分析,建立了往复密封的混合润滑理论模型,实现往复密封摩擦力、泄漏量等性能参数的仿真计算。
(2)选择典型的往复密封件斯特封开展往复密封台架验证试验,对往复密封最重要的性能指标摩擦力和泄漏量的仿真计算结果进行验证,发现两者吻合较好,说明数值模型的计算结果有较高的参考价值。
(3)斯特封的瞬时摩擦力随着介质压力的升高而增大,反装斯特封的泄漏量随着往复行程的累积而增加,但由于斯特封运动过程中的磨损等原因,其泄漏率并非线性增加,因此要实现累积泄漏量的准确预测是一件困难的事,需要综合考虑密封工作过程中材料和结构的的动态变化。

