水蒸气润滑螺旋槽干气密封性能分析*

(昆明理工大学化学工程学院 云南昆明 650500)

蒸汽轮机是目前广泛应用的原动机，蒸汽轮机效率的不断提高是一直追求的目标。采用各种密封(汽封)技术有效控制蒸汽轮机的泄漏(漏气控制)是提高其效率的一项重要措施[1]。研究人员利用多种类型的汽封，通过相应调整和整合多方面性能，达到优化汽封的效果，不仅提高了运行效率，还提高了机组的可靠性能。如曾宪平和任建兴[2]成功地将蜂窝式密封技术应用在汽轮机中。但研究也表明，超大或超小的芯格尺寸的蜂窝汽封的泄漏量仍很大[3]。

为了进一步减小汽轮机汽封泄漏量，可考虑采用螺旋槽干气密封方式。螺旋槽干气密封泄漏率很小，John Crane公司已有相应的产品[4]。在螺旋槽干气密封中，考虑实际气体效应对其性能有较大影响，许多研究人员对此进行了研究。宋鹏云等[5]以氢气为研究对象，分析了实际气体效应对螺旋槽干气密封性能的影响。孙雪剑等[6]应用RK方程求解了天然气实际气体的压缩因子，并用于分析天然气干气密封的性能。宋鹏云等[7]考虑实际气体效应，修正了可压缩流体润滑的雷诺方程，分析了实际气体效应对 T 形槽干气密封稳态性能和动态性能。许静等人[8]研究了气体热效应对干气密封性能的影响。

水蒸气润滑干气密封是一类特殊的干气密封，端面的润滑气体为水蒸气。一般认为，水蒸气不能当作理想气体，应考虑实际气体效应。本文作者通过近似解析法，以水蒸气为研究对象，考虑实际气体效应，分析了水蒸气润滑螺旋槽干气密封的稳态性能，包括端面开启力、气膜刚度、泄漏率、摩擦功耗、热平衡膜厚等。

1 几何模型与基本假设

1.1 几何模型

图1所示为典型的泵入式螺旋槽干气密封端面几何模型，其由槽区、台区和密封坝区组成。图中ro为密封环的外半径，rg为螺旋槽根处的半径，ri为密封环的内半径，ω为密封环旋转角速度。

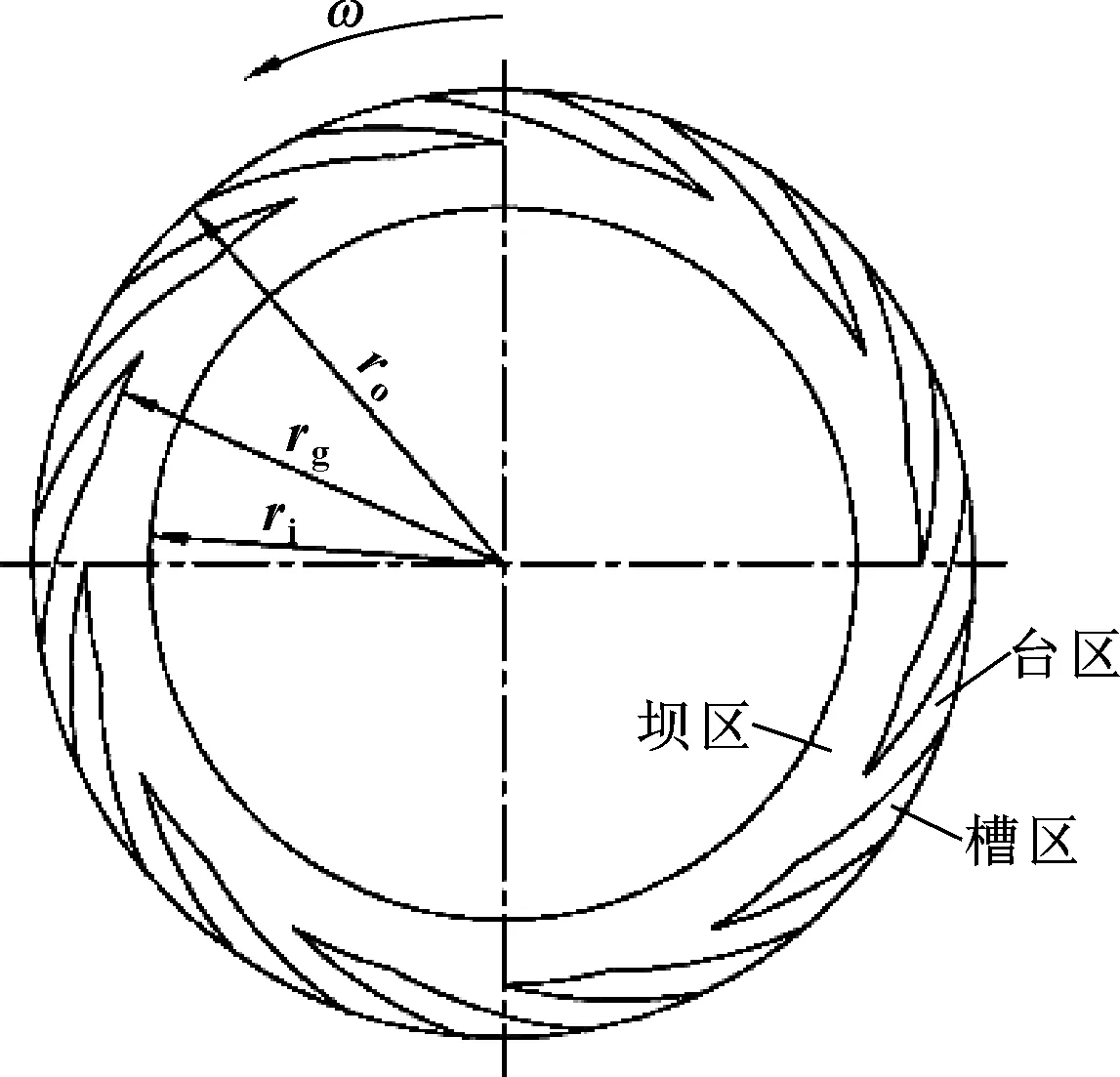
图1 泵入式螺旋槽干气密封端面几何模型

1.2 基本假设

文中研究基于以下基本假设[9]：

(1)不考虑润滑气体的体积力和惯性力；

(2)气体为牛顿流体，等温连续流动，黏度保持不变，流动为层流；

(3)两密封面非接触，严格对中；

(4)忽略表面粗糙度的影响；

(5)气体在固体界面无滑移。

2 数学模型

2.1 水蒸气的实际气体效应表达

实际气体效应表达可采用实际气体状态方程，如二阶维里方程、三阶维里方程、RK方程等各种方法，在压力较高的情况下，实际气体行为明显不同于理想气体，压缩因子Z不等于1。选取温度为300 ℃，针对水蒸气，各种计算方法得到的压缩因子如图2所示，其中的国际标准是指(IAPWS 97)，可由文献[10]获得。通过查取水蒸气的比容V，再用实际气体方程pV=ZRT求解出Z。在中低压下，RK方程与国际标准的平均误差为0.783 9% ，可以采用RK方程计算水蒸气的压缩因子Z。

图2 水蒸气的压缩因子

实际气体状态的R-K方程表达式[11]如下：

(1)

气体状态方程为

pV=ZRT

(2)

式(1)改写为

(3)

式(3)可得气体比容V的三次方程

(4)

将气体状态方程pV=ZRT代入式(4)可得

(5)

假定Z=x+1/3，则式(5)可化为可用卡尔丹公式求解的一元三次方程形式，即

(6)

令

可得

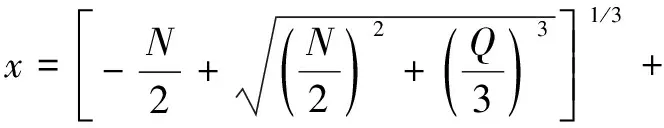
则

(7)

由于实际气体状态方程为

ρ=pM/(RTZ)

(8)

则实际气体的密度表达式为

(9)

其中，

(10)

(11)

2.2 实际气体效应修正的气膜压力

采用无限窄槽理论，依据Muijderman理论[12]，可得气体沿密封环的径向压力分布控制方程。

密封坝区：

(12)

螺旋槽的槽台区：

(13)

式中：μ为水蒸气的黏度，可从文献[10]查得；St为气体通过密封端面的质量流量；h为非槽区的气膜厚度；h1为槽区的气膜厚度，h1=h+t，t为螺旋槽的槽深；ω为密封环的旋转角速度；g1、g5、g7为螺旋槽函数，分别为

g5=(1+γH3)(γ+H3)+H3(1+γ)2cot2α

g7=(1+γ)H2(1+cot2α)(γ+H3)

式中：γ是台宽与槽宽的比值；α为螺旋角。

将式(8)分别代入方程(12)、(13)，可得到实际气体气膜控制方程。

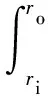
(14)

气膜刚度反映了抵抗干扰的能力，它是单位膜厚变化后引起的开启力变化，可在平衡膜厚h的基础上施加一个膜厚微扰hε，计算施加膜厚微扰后开启力Fε，则气膜刚度计算式为

(15)

3 结果分析与讨论

为具体研究水蒸气螺旋槽干气密封的性能，考虑水蒸气分别为理想气体和实际气体时，计算泵入式水蒸气润滑螺旋槽干气密封的密封性能。

3.1 计算案例

文中计算案例的结构参数和操作参数选自参考文献[13]。其中，ro=77.8 mm，ri=58.42 mm，rg=69.00 mm，α=15°，γ=1，t=0.005 mm；操作条件：pi=0.101 3 MPa，密封环的旋转角速度ω=1 087.08 s-1。

介质为水蒸气，其温度为300 ℃，等温流动。气体普适常数R=8.314 J/(mol·K), 温度300 ℃下的气体黏度μ=20.29×10-6Pa·s，临界温度Tc=373.946 ℃，临界压力pc=22.064 MPa。中低压情况下，压力对气体黏度的影响可以忽略。

利用式(9) 、(12) 、(13)可得到实际气体水蒸气的螺旋槽干气密封径向压力分布p(r)、泄漏率St及开启力F。同样地，设定压缩因子Z=1，可获得水蒸气理想气体的干气密封性能。

3.2 计算结果及分析

3.2.1 端面开启力

水蒸气在不同压力和不同气膜厚度下的端面开启力计算结果如图3所示。可以看出：在相同压力下，随着膜厚的增加，端面开启力减少；中低压时，水蒸气实际气体和理想气体的开启力几乎相等；高压时(5 MPa)，水蒸气实际气体的开启力略大于水蒸气理想气体。典型端面开启力数据如表1所示。可以看出，随着外压增大，表现为实际气体效应增强，相对误差增加。

图3 不同压力和气膜厚度下水蒸气开启力比较

压力p/MPa膜厚h/μm开启力F/kN实际气体理想气体相对误差ΔE/%0.52.039.962 408 819.959 853 74-0.025 647 11223.0515.103 620 4415.054 691 26-0.323 956 60855.0832.088 080 3831.833 985 79-0.791 865 964

3.2.2 气膜刚度

水蒸气在不同压力和不同气膜厚度下的气膜刚度计算结果如图4所示。

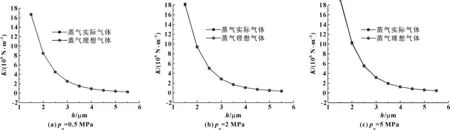
图4 不同压力和气膜厚度下水蒸气气膜刚度比较

可以看出：在相同压力下，随着膜厚的增加，气膜刚度减少；水蒸气实际气体刚度几乎等于水蒸气理想气体刚度。典型的气膜刚度数据如表2所示。可以看出，将实际气体考虑成理想气体，相对误差在0.5%左右。

表2 不同压力和气膜厚度下水蒸气气膜刚度比较

3.2.3 泄漏率

在不同压力和气膜厚度下，水蒸气泄漏率的计算如图5所示。可以看出：水蒸气的泄漏率，在不同压力下情况是不同的，在低压情况下(0.5 MPa)，随膜厚的增加，泄漏率先减小后增加；在中高压情况下，随着膜厚的增加，泄漏率增加。

如图5(a)所示，低压时，随着膜厚的增加，泄漏率先减小后增加，这一现象可以用密封坝泄漏率公式(16)解释。密封坝泄漏率公式[14]为

(16)

图5 不同压力和气膜厚度下水蒸气泄漏率比较

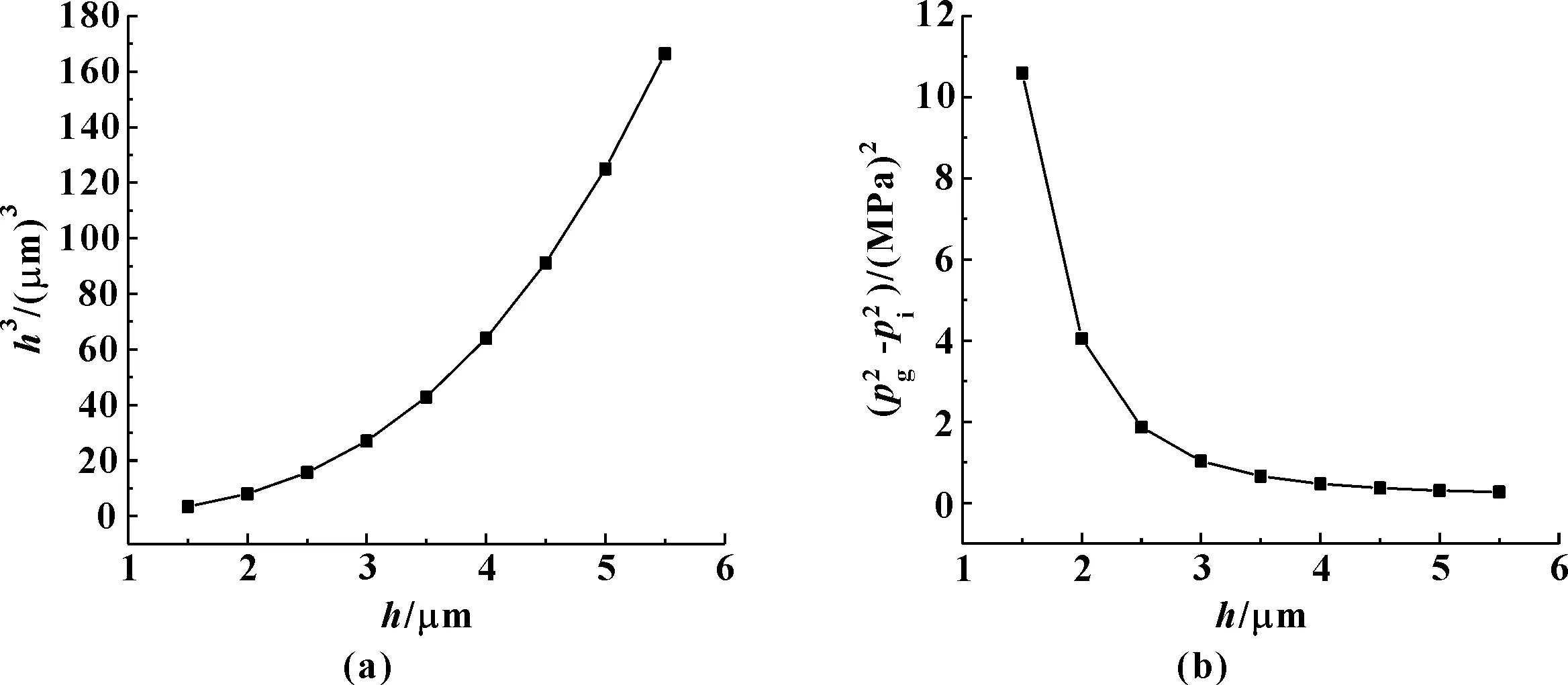
图6 低压下(p=0.5 MPa)膜厚h与泄漏率相关参数h3及的关系

如图5(a)所示，低膜厚时，实际气体与理性气体的泄漏率偏差略大。从表3可以看出，当压力为0.5 MPa时，低膜厚情况下，槽根压力大，压缩因子小，即实际气体偏离理想气体，此时相对误差较大，导致实际气体与理想气体的泄漏率偏差略大。

表3 气体通过密封端面泄漏率St的结果比较(0.5 MPa)

典型的泄漏率数据如表4所示，随着外径处压力po的增大，实际气体效应增加，表现为其相对误差加大。与开启力和气膜刚度相比，理想气体与实际气体泄漏率的相对误差要大得多，即实际气体效应对泄漏率的影响更为明显。

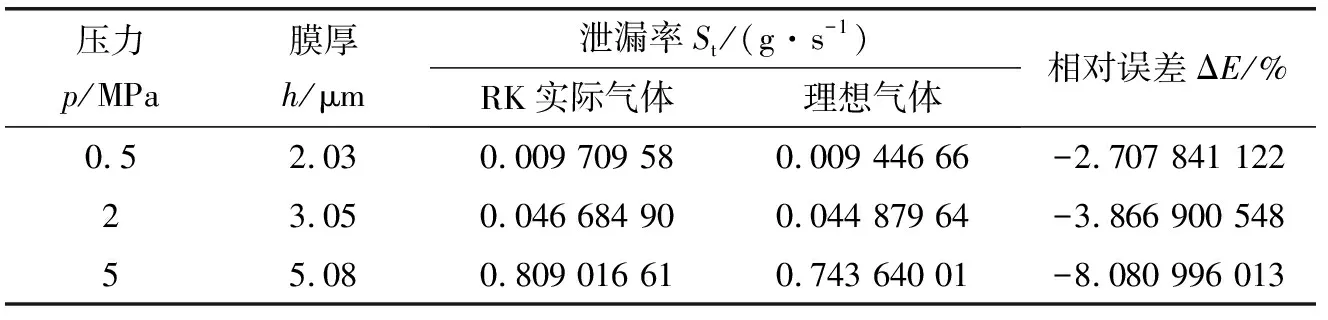
表4 通过密封端面的泄漏率St (RK 方程)

3.2.4 气膜摩擦力矩

直接利用牛顿剪切定律，总摩擦力矩公式[15]为

(17)

摩擦力矩随膜厚的关系如图7所示，可以看出，随着膜厚的增加，摩擦力矩随之减小。摩擦功耗是端面摩擦力矩与旋转角速度的乘积，因此摩擦功耗也是随着膜厚的增加而减小。

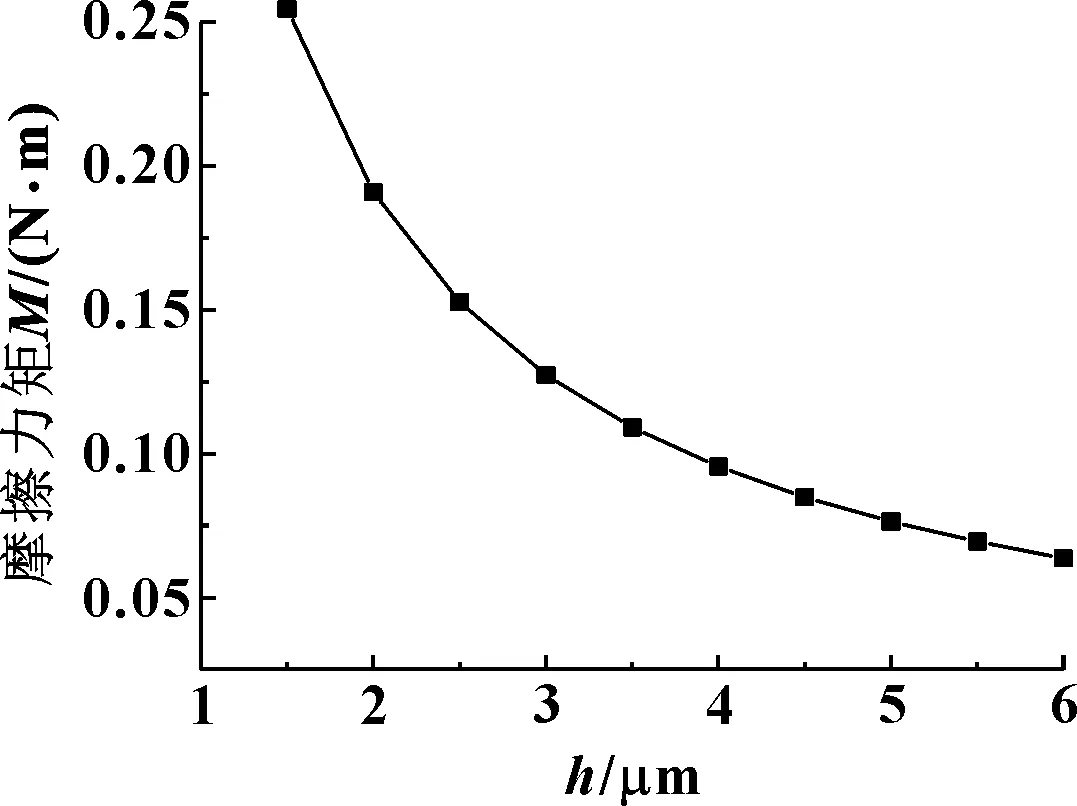
图7 端面摩擦力矩随膜厚的变化

3.2.5 热平衡膜厚

螺旋槽区和密封坝区在内的气膜因黏性剪切产生的热量[16]为

(18)

式中：ri为密封环内半径，mm；rg为槽根处半径，mm；ro为密封环外半径，mm；μo为外径处气体动力黏度，Pa·s；ω为密封环旋转角速度，rad/s。

气体因膨胀吸收的热量，设外径处气体温度为To，气体单纯因绝热膨胀，温度降为Ti，则吸收的热量为

(19)

式中:St为干气密封气体泄漏量，g/s；cp为气体比热容，J/(kg·K)；Rc为气体常数，J/(kg·K)；k为气体绝热指数。

假设端面间气体为理想气体，流动为绝热过程，根据热力过程方程可得

(20)

将式(20)代入式(19)，可以得到

(21)

由式(21)可知，对于给定操作参数的干气密封，气体单纯因膨胀吸收热量只与泄漏量St有关。依据前面计算泄漏率的方法，求解泄漏率，从而算出气体因膨胀吸收的热量W。剪切发热和膨胀吸热随膜厚的关系如图8所示。

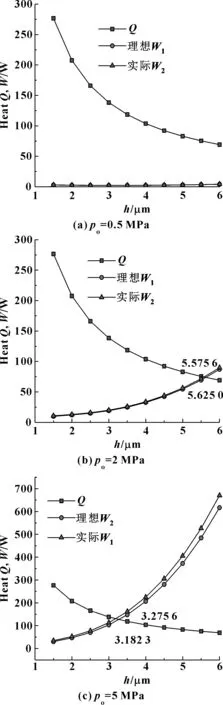
图8 剪切发热和膨胀吸热随膜厚的变化

当压力为0.5 MPa时，如图8(a)所示，水蒸气考虑为理想气体时，在常见的工作气膜厚度范围内，剪切发热速率始终大于膨胀吸热速率，不能达到热量平衡，无法获得热量平衡膜厚。此时，气膜温度要升高。

当压力为2 MPa时，如图8(b)所示，单位时间内，气膜剪切产生热量Q，实际气体膨胀吸热W1，理想气体膨胀吸热W2。经数据拟合得到：

Q=3.072h2-54.157h+312.67

(22)

实际气体膨胀吸热

W1=7.956 5h2-18.915h+55.022

(23)

理想气体膨胀吸热

W2=7.316 1h-17.172h+48.707

(24)

分别联合式(22)、(23)及式(22)、(24)求解得出热量平衡膜厚。水蒸气考虑为理想气体时，热平衡膜厚ho=5.625 0 μm，即达到热量平衡，端面气体总体上处于一个等温状态；水蒸气考虑为实际气体时，热平衡膜厚ho=5.575 6 μm，即达到热量平衡，端面气体总体上处于一个等温状态。

当压力为5 MPa时，如图8(c)所示，单位时间内的剪切发热量Q不随压力变化，剪切产生热量Q同式(22)，只需拟合实际膨胀吸热W1及理想膨胀吸热W2。

实际膨胀吸热

W1=1.023 5h2-2.742 6h+13.754

(25)

理想膨胀吸热

W2=0.985 4h-2.545 4h+12.798

(26)

分别联合式(22)、(25)及式(22)、(26)求解得出此时的热量平衡膜厚。水蒸气考虑为理想气体时，热平衡膜厚ho=3.275 6 μm；水蒸气考虑为实际气体时，热平衡膜厚ho=3.182 3 μm。

4 结论

(1)选取温度为300 ℃，适宜用RK方程进行压缩因子Z的计算。并分别与国际标准进行对比，可以看出，中低压下，用RK方程求解压缩因子Z是可行的。

(2)典型端面开启力实际气体与理性气体的相对误差在0.8%左右，气膜刚度的相对误差在0.5%左右。与开启力和气膜刚度相比，理想气体与实际气体泄漏率的相对误差要大得多，即实际气体效应对泄漏率的影响更为明显。

(3)随着膜厚的增加，摩擦力矩随之减小。实际气体行为对摩擦力矩无影响。

(4)当温度为300 ℃，压力为2 MPa时，水蒸气考虑为理想气体时，热量平衡膜厚ho=5.625 0 μm；考虑为实际气体时，热量平衡膜厚ho=5.575 6 μm。压力为5 MPa，理想气体状态下，热量平衡膜厚ho=3.275 6 μm；实际气体状态下，热量平衡膜厚ho=3.182 3 μm。