基于热耦合的滑动轴承两相流场特性数值研究*
(东南大学火电机组振动国家工程研究中心 江苏南京 210096)
滑动轴承是汽轮机、压缩机等大型旋转机械的重要支撑部件,轴承内部润滑油流动是复杂的剪切流,伴有润滑油与轴颈、轴承的摩擦以及润滑油空化等现象,其中摩擦产生的热量直接影响润滑油黏性,进而影响轴承的压力分布、承载力、动力特性等宏观特性。因此,结合传热学、气液两相流理论对深入研究轴承内部润滑油流动具有重要的意义。
目前,轴承动力润滑理论主要可分为基于雷诺方程的方法和计算流体方法。其中,基于雷诺方程的方法获得了广泛的应用,但在考虑油膜径向流动、回流与进油混合作用、空化效应的影响方面,存在一定的局限性。LUND和TONNESEN[1]基于雷诺方程的温度计算结果与实验数据在收敛区基本相符,但是在发散区有较大的差异。MITSUI等[2]和FERRON等[3]对比了实验和理论分析得到的滑动轴承热动力特性。上述的轴承热动力特性研究均没有考虑油膜空化效应,而大量的实验表明油膜发散区是油与汽的混合[4-5]。
计算流体力学(CFD)能求解复杂的几何形状、物性参数、边界条件等特性。GUO等[6]使用CFD计算了轴承的静特性和动力特性。DELIGANT等[7]利用CFD分析了轴承的压力场和温度场。郭瑞、张楚等人[8-9]运用CFD技术研究了空化效应对轴承的影响。汤世炎、郭红等人[10-11]对动静压轴承的油膜温度场进行了分析,但选取的绝热边界与实际情况存在偏差。张振山等[12]研究表明,不同热边界条件对热流体动力润滑分析的结果有较大的影响。
本文作者综合考虑油膜的能量方程、转子和轴瓦的导热特性,以及润滑油的黏温效应和两相流特性,建立滑动轴承流场三维CFD计算模型,分析轴承温度场分布、压力分布等特性,为工程应用和轴承设计提供一定的参考。
1 轴承转子热耦合模型
1.1 流固热耦合模型
轴承间隙内润滑油为强烈的剪切流动,流体微团摩擦产生热流,通过求解油膜能量方程、转子和轴瓦的热传导方程,耦合转子与油膜、轴瓦与油膜边界的热量传递,得到轴承的温度场。
润滑流体能量方程:

(1)
转子和轴瓦导热方程:

(2)
润滑油和转子、轴瓦之间的耦合壁面传热条件:
Tf=Ts
(3)
qf=qs
(4)
转子、轴瓦与空气的对流换热边界:
q=ha(Ta-Ts)
(5)
式中:下标k代表第k相属性;f、s、a代表流体、固体、空气属性;α为体积分数;ρ为密度;H为显焓;v为速度;p为相对压力;λ为导热系数;T为温度;q为热流量;h为对流传热系数。
1.2 油汽两相流模型
根据目前的研究,油膜发散区润滑介质为复杂的气液两相流形态,文中采用混合模型计算两相流特性。
1.2.1 两相流控制方程
油膜连续性方程和动量方程:
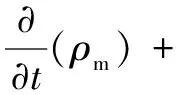
(6)

(7)
两相流混合密度和黏度:
ρm=αvρv+αgρg+(1-αv-αg)ρl
(8)
μm=αvμv+αgμg+(1-αv-αg)μl
(9)
润滑油黏温方程:
μl=μ0eβ(T0-T)
(10)
式中:下标m、v、g、l分别代表混合物属性、汽体相属性、气体属性、润滑油属性;g为重力加速度,F为体积力;μ为动力黏度;vdr,k为漂移速度;μ0为参考温度T0下的动力黏度;β为黏温系数。
1.2.2 全空化模型控制方程
在发散区油膜会发生破裂,根据全空化模型[8],可以得到两相流中的气相输运方程:
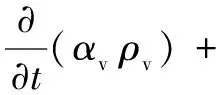
(11)
当p≤pv时
(12)
当p≥pv时
(13)
式中:Re为空化相变率;Rc为凝结相变率;vch为特征速度;σ为表面张力系数;Cε与Ce为经验系数。
2 计算模型网格结构和验证
2.1 模型网格划分
文中研究的轴承的几何参数如表1所示。
文中计算区域包括转子、油膜、轴瓦3个部分,转子表面一部分与油膜耦合,其余部分与空气进行对流换热;轴瓦的内表面与油膜耦合,外表面与空气进行对流换热。润滑油从水平方向(X轴)的两侧管道进入,从两端(Z轴)流出,转子旋转方向与Z轴正向成右手定则。图1(a)所示为整体模型网格图,图1(b)所示为其中的油膜网格图,其中,X轴负方向水平位置进油口为进油口1,正方向为进油口2;周向角度θ沿旋转方向计算,起始0°设置为X轴负方向。

表1 轴承几何参数
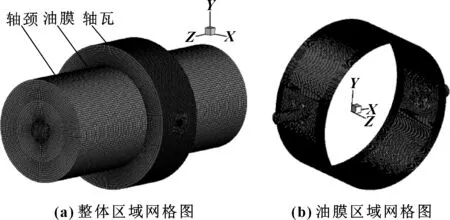
图1 计算区域网格图
根据结构特点对计算区域进行网格划分,轴瓦的周向、轴向、径向的网格节点配置为360×60×12,转子的节点配置为120×180×20。油膜的周向、轴向分别取360、120个节点。相对其他几何参数,油膜径向尺寸数量级很小,模型的网格质量和经济性主要由径向网格数量决定,因此在径向取10、15、20个节点进行网格独立性检验。表2显示网格数大于1 655 k时,最大压力和承载力变化较小,满足计算精度,后续计算采用方案2的网格配置。

表2 不同网格方案下的计算结果
2.2 轴承转子热耦合模型的验证
文献[1]对轴承热动力特性进行了详细研究,将文中的轴承温度场计算结果与文献[1]的实验结果进行比较,如图2所示。计算时采用了文献[1]的参数:轴承半径50 mm,轴承宽度55 mm,转子跨距458 mm,半径间隙668 μm,偏心率0.55;转速5 000 r/min,进口油温50 ℃。

图2 实验和计算结果对比图
由图2可知:(1)计算温度和实验测量的温度分布总体上一致,最大偏差不超过2 ℃;(2)在收敛区,温度在周向10°~150°迅速上升,最高温度在周向150°处,之后温度迅速下降,与实验测量值很好地吻合;(3)在油膜发散区,温度在周向190°~220°上升,油膜间隙变大,润滑油摩擦生热作用减弱,温度在周向220°~350°下降。文中考虑了发散区的油膜空化效应,因而计算结果与实验测量值吻合较好。
3 计算结果及分析
以某轴承实验台的轴承为研究对象,其主要参数为:轴承偏心率ε=0.5,偏位角49.8°,转速1 000 rad/s;基准压力101 325 Pa,进油表压108 kPa,出口表压为0;润滑油密度ρl=876 kg/m3,50 ℃动力黏度μ=0.012 5 Pa·s,黏温系数β=0.032 79[13],比热容c=2 000 J/(kg·℃),导热系数λ=0.15 W/(m·℃),汽化压力为3 500 Pa;轴瓦和转子的导热系数λs=50 W/(m·℃),轴瓦和转子表面的对流换热系数h=50 W/(m·℃),环境温度20 ℃[1]。
3.1 温度场分析
图3示出了轴瓦内壁温度分布,可知:(1)轴瓦的最高温度75 ℃位于周向147°,在最小膜厚下游,最低温度58 ℃位于周向0°,靠近进油口1,温度分布总体趋势与文献[2]的实验结果符合;(2)由于动压效应,油膜受到剪切和摩擦,产生的热量使下轴瓦从进油口1到最小膜厚处的温度从60 ℃逐渐上升到75 ℃;(3)进油口2的温度迅速下降14 ℃,这是因为低温进油对轴瓦的冷却作用;(4)低温进油与循环油混合作用,使得油温显著降低,而且由于空化效应,发散区流体密度、黏度下降,上轴瓦的温度变化较少;(5)下轴瓦内壁的轴向温度基本不变,由于发散区复杂的两相流,上轴瓦内壁的温度呈现出明显的中间高两边低。

图3 轴瓦内壁温度分布图
3.2 轴承转子热耦合模型和绝热边界模型的比较
图4给出了文中模型与绝热边界模型[11]温度计算结果的比较,采样线为图3中轴瓦内壁的中心线。

图4 轴瓦内壁采样线温度分布
图4表明,绝热模型的温度分布明显高于文中模型,平均约高出10%,这是因为绝热模型忽略了传热损失,与实际情况存在偏差。
由图5可知:(1)2种模型的压力分布趋势相同,最高压力幅值不同;(2)绝热模型的压力计算结果比文中模型偏小,绝热模型的平均温度较高,由黏温效应可知,润滑油黏度变小,动压效应减弱。

图5 轴颈表面压力分布
3.3 进口油温对轴承特性的影响
上述温度场分析表明进口油温对轴承特性有很大的影响,而且在现场工作条件下,油温作为调整轴承特性的主要手段,因此文中研究了不同进口油温对轴承特性的影响,结果如图6所示。

图6 不同进口油温下的轴承特性(n=1 000 rad/s)
由图6(a)、(b)可知,油膜最大压力、油膜承载力随着进口油温升高逐渐降低,温度升高30 ℃,油膜最大压力、油膜承载力降低了约25%;文中模型的油膜最大压力、油膜承载力高于绝热模型,但是随着油温增加,两者偏差逐渐减小。
由图6(c)可知,随着油温提高,文中模型和绝热模型的润滑油温升都逐渐下降,这是因为高温的润滑油黏度小,剪切应力小,摩擦产生的热量少。
图6(d)中,空化体积比是气相区域体积占油膜体积的比例。图6(d)表明,随着油温升高,空化体积比逐渐减少,油膜发散区的空化效应减弱;总体上,文中模型的空化体积比低于绝热模型,但是随着油温升高到55 ℃,两者偏差逐渐减小。
综上所述,进口油温对轴承特性有很大的影响,轴承工作时应合理选用进口油温。
4 结论
(1)考虑轴承热传导和空化效应建立的轴承转子热耦合系统模型与实际工作状况更加符合。
(2)轴瓦的最高温度位于最小膜厚下游,下轴瓦的温度逐渐升高,而上轴瓦的温度变化较少。
(3)热耦合系统模型的压力分布趋势与绝热模型相同,绝热模型的压力计算结果比热耦合系统模型偏小。
(4)随着进口油温升高,油膜最大压力、承载力、空化体积比、进出口温差下降,并且热耦合系统模型与绝热边界模型的计算结果偏差变小。

