基于U型统计量的泊松过程参数变点检验

范梓淼, 田梦琴

(新疆农业大学 数理学院，新疆 乌鲁木齐 830052)

引 言

变点问题是统计学中的热门研究方向，在金融、医学、气象学和计算机领域等方面有广泛地应用。该问题源于质量检测与监控。现今，变点的应用不再局限于工业质量的检测中，更广泛地被应用于经济、医学、计算机等领域。[1]例如，在医学中，心电图韵律的检测及流行病中传染病的传染率检测；计算机领域中，图像识别和图形边界的判断等都依赖于变点的发展使用。另外，在生态环境和突发灾难方面，变点研究方法也发挥着重大作用。因此对变点问题的深入研究有着重大意义。

泊松过程由法国数学家Poisson Simeon-Denis首先提出的，是一个时间连续状态离散随机过程，是记录随机事件发生次数累加的独立增量过程[2]。泊松过程不仅是作为计数过程的重要随机过程模型，也是重要随机过程的特例，且通过泊松过程可以构造其他独立增量过程，所以其在随机过程中占重要位置。研究泊松过程变点问题，也为进一步研究随机过程奠定了一定基础，是有意义的。本文基于泊松过程，采用U统计量方法研究参数变点的假设检验问题。

U统计量是由W.Hoeffding于1948年引入统计学研究中的，它被广泛地应用于非参数统计学研究中。缪柏其、魏登云通过U统计量研究了刻度参数变点的统计推断[3-5]；Horváth通过U统计量讨论了分布函数的变点问题[6]；Csörgö,M，Orasch等在变点问题研究的其他应用中都使用了U统计量[7]。

U统计量的定义为：设X1,X2,…,Xn为独立随机变量，φ(x1,x2,…,xm)为其某一对称函数，mn。则以φ(x1,x2,…,xm)为核构造的统计量

称为U统计量。

1 泊松过程参数变点模型

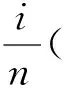
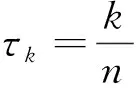
X1,X2,…Xτ0～P(λ1)，X(τ0+1),…Xn～P(λ2)

(1)

其中P(λ)为参数λ的泊松过程。

关于泊松过程变点的问题可以化为如下假设检验问题:

H0:λ1=λ2vsH1:λ1≠λ2

(2)

2 U统计量法

为叙述方便，首先给出以下定义

设X1,X2,…,Xmi.i.d～F，Y1,Y2,…,Yni.i.d～G，

对于对称函数φ(x1,x2,…,xm;y1,y2,…,yn)，定义

φij(X1,X2,…,Xi;Y1,Y2,…,Yj)=E[φ(X1,X2,…,Xm;Y1,Y2,…,Yn)|X1,X2,…,Xi;Y1,Y2,…,Yj]，

σij2=Varφij(X1,X2,…,Xi;Y1,Y2,…,Yj)，1im，1jn。

定理1 若X1,X2,…,Xn为来自泊松过程的独立随机变量，定义

若k满足

(3)

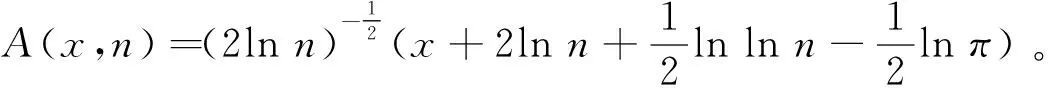
为了证明定理1，需指出以下引理。

引理1[8]设随机变量X1,X2,…,Xn，i.i.d.～F，Var(X1)<，φ(x,y)为R2上的二元可测函数，且|φ(x,y)|bEφ(Xi,Xj)=0,i≠j。

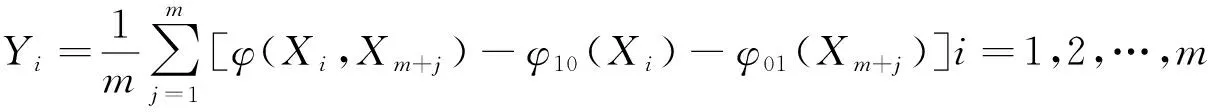
则存在常数C>0，对∀ε>0，当m充分大时，

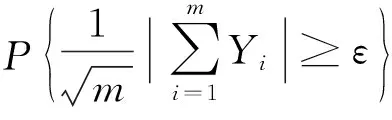
引理2[8]设X1,X2,…,Xni.i.d～F，φ(x,y)为R2上的二元可测函数，且

|φ(x,y)|b，Eφ(Xi,Xj)=0,i≠j，Eφ(Xi,Xj|Xi)=0。

设Un是以φ(x,y)为核的U型统计量，则对∀ε>0，δ>0，当n充分大时，有

由Uk的定义知

-φ01(Xj1)-φ01(Xj2)+φ10(Xi1)+φ10(Xi2)+φ01(Xj1)+φ01(Xj2)]

▷U1+U2

定理2 若n和k满足定理1的条件(3)，则

证明:

-φ12(Xi2;Xj1,Xj2)+φ12(Xi1;Xj1,Xj2)+φ12(Xi2;Xj1,Xj2)+φ02(Xj1,Xj2)-φ10(Xi1)-φ10(Xi2)

-φ01(Xj1)-φ01(Xj2)]

-φ12(Xi1;Xj1,Xj2)]

由φ(Xi1,Xi2;Xj1,Xj2)定义知，|φ(x,y)|

∴当Xk+1,Xk+2,…,Xn给定时，由引理2可得，

同理，当X1,X2,…,Xk给定时，

由引理1

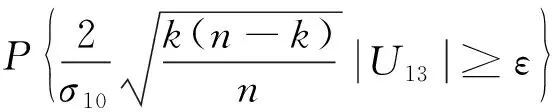
U14和U15符合引理2条件，所以有，

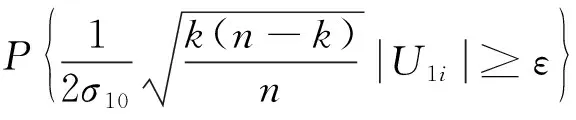
∴存在c(ε)，使得

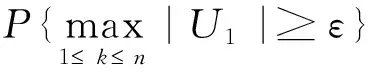
由定理1条件知，当n充分大时，上述不等式右边小于n-2，由Borel-Cantelli引理知，该定理成立。

其中c>0为任一常数。

引理4[8]若{Z(t),t≥0}为一平稳高斯过程，且

ρ(τ)=E[Z(t)Z(t+τ)]=1-|τ|+ο(|τ|),τ→0

定理1证明:

由定义知

设{B(t),t≥0}为标准布朗运动，进行如下运算，有

由引理4和定理条件，有

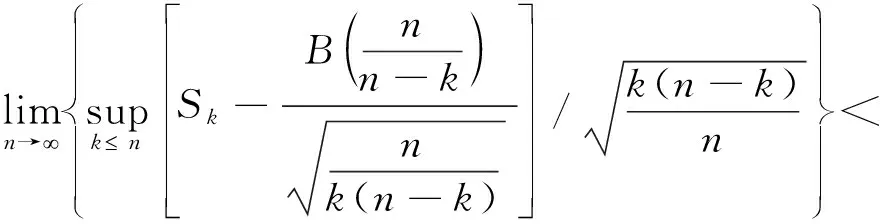
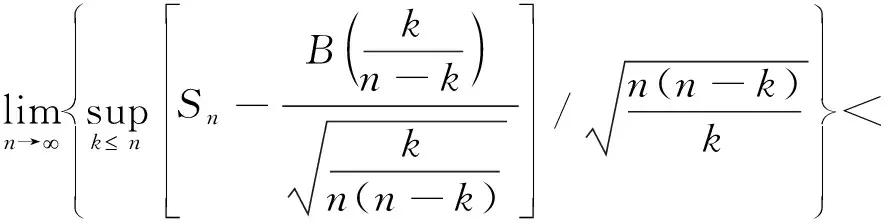
作高斯过程Z(t)=B(t)-B(t-1)，易知Z(t)为平稳过程，

EZ(t)=0

及

∴由引理5，可得

综上，

该定理给出了检验假设模型(2)的方法，假设给定显著性水平为α。由

exp{-2e-x}=1-α，

解得

那么当且仅当

时，拒绝原假设，也就是接受有变点。

本文构造适应于泊松过程的检验统计量，并证明了该检验统计量的极限分布为第一型极限分布。如果令k从小到大增加，则|Uk|会增大，当到达变点位置τ0时，|Uk|应该会出现最大值；如果k继续增大，|Uk|又会减小，因此，参数变点位置的估计可选取使得检验统计量最大的点作为。

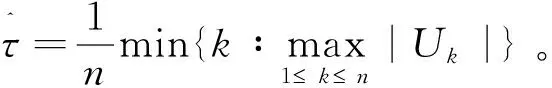
3 结 论

变点分析理论在科学研究和实践应用等方面都有着快速的发展。变点问题的统计推断就是根据具体的背景，对变点做出估计，并对估计量的性质进行统计分析。本文在泊松过程模型下，对其参数的变点进行假设检验，在存在变点的情形下，对变点位置做出了估计。对深入研究泊松过程有一定的帮助。