具有指数项的高维循环差分方程的动力学性质

(湖南大学 数学与计量经济学院,湖南 长沙 410082)

随着计算机的迅速发展,差分方程理论不仅在数值分析等领域中有广泛的应用,而且成为通信理论、现代控制论、神经网络科学和社会经济活动等的重要数学工具。差分方程已成为数学领域特别是动力系统研究中的一个重要分支,理论意义和应用价值重大，得到了深入研究[1-6]。指数型差分方程是用来描述自然现象变化规律的重要工具之一。随着生物数学、现代物理、管理科学等自然科学及边缘性学科的不断发展，近年来，提出了许多应用指数型差分方程来描述的数学模型[7-13]，如[14]

xn+1=axn+bxn-1e-xn,

其中参数a,b∈(0,+∞),初始值x-1、x0为正数,n=0,1,2,…。文献[15]中进一步把文献[14]中的结果推广到一类指数型差分方程，即

其中c、d也是正常数，并且初始值y-1、y0也是正值。由于总是有多个物种在同一区域中同时生存，因此，种群间存在诸如捕食、竞争、协作等相互作用。研究单种群或两种群模型的目的之一是为研究多种群间的相互作用奠定基础。上述模型耦合的多种群生物数学模型为

(1)

1 主要结果与证明

定理1若系统中正实数ai、bi满足

ai,bi∈(0,1),i=1,2,…,m,

(2)

则系统(1)的任一解是有界的。

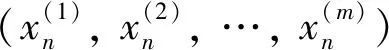
因为fi(0)=M,

所以fi(x)≤M,x∈[0,M]。由此可推出

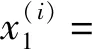
定理21)若系统(1)中正实数ai、bi满足条件(2)，并且

(3)

2)若系统中正实数ai、bi满足条件(2)，并且

(4)

则零平衡点(0,0,…,0)是系统(1)的唯一非负平衡点。

证明：1)考虑函数

hi∶+→+,

显然，hi(x)严格单调递增。定义

其中I为恒等函数，∘为函数的复合运算。令xm+1=x1考虑代数方程组xi+1=hi(xi),i=1,2,…,m，可推出对任意j∈{1,2,…,m}有

hj(xj)+xj]。

定义

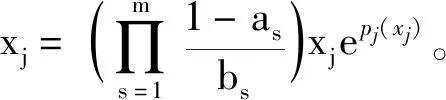
定理3若系统(1)中正实数ai、bi满足条件(2)，并且ai+bi<1,i=1,2,…,m,

(5)

则系统(1)的任意解收敛于零平衡点。

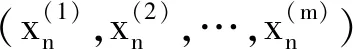
(6)

考虑差分方程系统

(7)

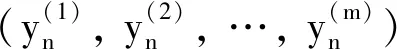
则由式(6)、(7)可得

(8)

下面证明系统(7)的任一正解收敛于零平衡点(0，0，…，0)。

系统(7)等价于系统

(9)

A=

根据定理的已知条件，可选取一个常数ε>0满足

(10)

(11)

其中

T-1AT=

由式(10)可知，εm<1且

从而有|T-1AT|<1。

设λi是矩阵A的特征值，则

|λi|≤|T-1AT|<1,i=1,2,…,2m，

因此，系统(11)的任一正解收敛于零平衡点(0,0,…,0)从而推出系统(9)的任一正解收敛于零平衡点(0,0,…,0)。由式(8)可知，定理的结论成立。

2 结论

高维非线性差分方程的研究既有理论方法的困难，也有几何描述和数值计算的困难，因此，高维非线性差分方程的研究难度比低维情形的大得多，相关研究工作也很少。本文中在借鉴已有研究理论的基础上，对一类可作为生物数学模型的高维指数型差分方程的动力学行为进行了有益的研究和探索，不仅拓展了差分方程模型，也突破了维数的限制。本文中的主要结果都是在充分性条件下获得的，还有进一步改进的空间，今后将对方程中的参数个数及单个方程进行进一步拓展和深入研究。