拟阵的独立集构成的偏序集
(河北大学 数学与信息科学学院,河北 保定 071002)
虽然拟阵在组合理论中很重要[1-3],但是这并不意味着拟阵可以覆盖组合理论的所有方面。组合理论中的许多方面可以用拟阵清晰地解释。这些解释成为组合数学与更多数学主流领域的连接带。将偏序集理论[4-5]应用到拟阵的研究是一条成功之路[1-3,6-14]。此外,借助于偏序集理论,可以建立与拟阵有关的一些新框架[6-7,14]。拟阵具有几何格表示,反之,每个几何格是简单拟阵;但是并不是每个拟阵都是简单的,即有些拟阵不能由几何格给予特征。另外,Welsh[2]指出,拟阵最著名的算法性质与贪心算法有密切关系。贪心算法已被广泛地应用和研究[1,2,15-16]。拟阵的贪心算法特征是由拟阵的独立集所描述的[2]。为了寻找拟阵的更多算法特征,并将拟阵的应用范围拓广,考虑到每个格都是偏序集,因此,本文中考虑将贪心算法与偏序集结合,以用于挖掘拟阵的更多算法结果,该实现首先需要解决拟阵与偏序集之间的关系问题,才能进一步探索拟阵新的特征。在开始研究之前,应注意以下几点。1)拟阵由其独立集族所定义[1-3]。2)Boolean格已经用于研究任意基数集上的拟阵之独立集的问题[17-19]。3)拟阵是一种特殊的独立结构[20]。4)因为与独立集有关,所以Boolean格已被用于拟阵的研究[14],另外,Mpi-空间和独立空间可以分别用偏序集予以特征化[19,21]。偏序集理论与拟阵也有成功的结合[1-2,22]。5)对于任意拟阵M=(S,T(M)),其中S为有限集,T(M)为M的独立集族,可以得到与该拟阵有关的偏序集(T(M),⊆)。
上述这几点蕴含着用拟阵的独立集对应的偏序集探讨拟阵的必要性。本文中利用偏序集理论将拟阵特征化,该方法不同于已有的发现拟阵的特征的研究方法,例如,拟阵的几何格特征的发现方法[1-3]。
为了使影响拟阵应用的几何格条件减弱为更广泛的数学结构——偏序集,本文中通过拟阵的独立集族构建偏序集,用偏序集配合Boolean格搭建拟阵,在同构意义下实现用偏序集的性质将拟阵特征化。首先提出在一定条件下,偏序集P能在同构意义下定义拟阵M(P);在同构意义下,挖掘满足一定条件的偏序集与无环拟阵之间的关系,并将结果与著名的拟阵、几何格之间的结果进行比较。
1 预备知识
1.1 符号
本文中所有讨论均为有限。|A|为集合A的基数;2A为A的幂集;max{|Xi| ∶i=1,2,…,n<∞}为集合{|Xi| ∶i=1,2,…,n<∞}中的元关于自然序的最大值。
在偏序集P中,Max(P)是P中极大元集合;若x和y是P中不可比元,则记为x‖y。
∨和∧分别为格中的并和交2种运算。
1.2 定义
1)设S为有限集,T 为S的子集族。如果T 满足以下条件,那么称(S,T )为拟阵(matroid),记为M=(S,T ),T 记为T (M),其中的元称为独立集。
①∅∈T。
②若X∈T且Y⊆X,则Y∈T。
③若U、V是T中的元且|U|=|V|+1,则存在x∈UV满足V∪{x}∈T。
若S的子集X不属于T,则称X为M的相关集。M的基是M的极大独立集。M的秩函数是函数ρ∶ 2S→,定义为ρ(A)=max{|X| ∶X⊆A,X∈T },A⊆S。S的秩称为拟阵M的秩,记为ρ(M)。[2]
2)拟阵M的环(loop)是S的元素x,若{x}为相关集;称S的2个元x、y为平行的(parallel),若它们均不是环,但是{x,y}为相关集。
称无环、无平行元的拟阵为简单拟阵(simple matroid)。
2个拟阵M1=(S1,T1)和M2=(S2,T2)称为同构的(记为M1≅M2),如果存在双射f∶S1→S2满足A∈T1⟺f(A)∈T2。[2]
3)若偏序集P有唯一的最小元,通常将该元记为0,则将覆盖0的元称为原子(atom)。P的全序子集称为P的链(chain),即{x0,x1,…,xk}是一个链当且仅当x0 4)格L称为Boolean的当且仅当L为含最小元以及最大元的有补分配格。[4] 本节将研究拟阵的独立集族由包含关系所构成的结构,并探讨偏序集与拟阵之间的关系。这些关系的意义和价值在于它们可以将拟阵框架下的结果与偏序集框架下的内容相互转化。 令M为S上的拟阵,T (M)为其独立集族,B(M)为其基族。令P (M)代表(T (M),⊆)。 性质11)P (M)以{∅}为其最小元。 2)P (M)的原子集是M中秩等于1的独立集的全体。 3)a∈Max[P (M)]当且仅当a∈B(M)。 4)X在P (M)中覆盖Y的充要条件是X,Y∈P (M),Y⊆X并且|X|=|Y|+1。 引理11)在P (M)中所有的极大链有相同的长|B|,此处B∈B(M)。 2)P (M)中的每个元素I以M的秩函数ρ(I)为其高度。 3)对于任意基B∈B(M),在P (M)中的区间[0,B]是Boolean格,此处0={∅}。另外,对任意的I∈P (M),I是P (M)的一些原子的并。 4)对于任意的I,J∈P (M),如果|J|=|I|+1成立,那么存在j∈JI满足I∪{j}∈P (M)。 证明:由M中基的定义以及M中秩函数的定义,易得1)、2)和4)。根据性质1中的3),可以导出B∈P (M)。对于任意的X⊆B,有X∈P (M),因此,得到 (2B,⊆)⊆P (M)和(2B,⊆)=({Y∈T (M)∶Y⊆B},⊆),从而,3)成立。引理1证毕。 引理1的3)表明Boolean格将会揭示偏序集与拟阵之间的一些内在关系。为了验证该结论,需要下面的引理。 引理21)有限偏序集P有最小元0。设h为P的高函数,Θ为P中的原子集。对于x∈P,设Xx={a∈P∶a∈Θ且a≤x}。若P满足如下条件2)— 4),则存在定义在Θ上的满足(T (M(P)),⊆)≅P的拟阵M(P),并且M(P)无环。 3)对于任意b∈Max(P),[0,b]≅(2{y∈Θ ∶y≤b},⊆)成立。 4)对于任意z,t∈P,若h(t)=h(z)+1成立,则存在y∈XtXz满足z∨y∈P和Xz∪{y}={a∈P∶a∈Θ且a≤z∨y}。 证明:根据条件1),h和Θ二者都有意义。设I(P)={X⊆P∶存在x∈P,使得X= {y∈P∶y是P的原子,并且y≤x} }。 首先证明(Θ,I(P))是拟阵。 由条件1)可知,0∈P成立,但是0不是原子。根据条件2),这意味着∅∈I(P),因此,对于I(P),在1.2节1)中的条件①成立。 设U、V∈I(P)且|V|=|U|+1。根据I(P)的定义,可知u=∨U∈P且v=∨V∈P,另外,Xu=U和Xv=V成立。根据条件2)和|V|=|U|+1,得到h(v)=h(u)+1。利用条件4)可得y∈XvXu=VU满足u∨y∈P和Xu∨y=U∪{y}。由此可知,U∪{y}∈I(P),因此,在I(P)中,1.2节1)中的条件③成立。 根据拟阵的定义,(Θ,I(P))是拟阵。为了简单起见,记(Θ,I(P))为M(P)。 证明(I(M(P)),⊆)≅P。因为I(M(P))是I(P),所以证明(I(P),⊆)≅P。 事实上,易知I(P)={Xx∶x∈P}。 设x∈P。由条件2),有且仅有X∈I(P)满足∨X=x;反之,若∨X=x,则X∈I(P);因此,定义为x→Xx的映射φ∶P→I(P)是有意义的。根据I(P)的定义,对于x∈P,有I(P)={Xx∶φ(x)=Xx}。根据条件2),φ为双射。下面证明φ是同构。 容易得到a=0∈P的充要条件是φ(a)={∅}。 设x,y∈P,则φ(x)=Xx=X={a∶a∈Θ且a≤x}且φ(y)=Xy=Y={a∶a∈Θ且a≤y}。 若x≤y,由条件2)可知x=∨X以及y=∨Y。根据x≤y可知,若a∈X,则a∈Y,因此X⊆Y。反之,设I,J∈I(P)且I⊆J,则根据条件2)和I(P)的定义可得,存在i,j∈P满足i=∨I和j=∨J。另外,可以确定I={a∈Θ∶a≤i}且J={a∈Θ∶a≤j}。由i∈I⊆J可得i∈J,进而有i≤j,即x≤y当且仅当X⊆Y。 类似地,可以证明,在P中x‖y的充要条件是在I(P)中X‖Y,此处∨X=x且∨Y=y。 从而,φ是在P与(I(P),⊆)之间的同构映射。 证明M(P)无环。由于φ为双射,因此x∈Θ⟺Xx={x}∈I(P)。由此可知,M(P)无环。引理2证毕。 通过分析引理2条件1)— 4),发现如果一个偏序集不满足条件1),则不存在拟阵M满足(T (M),⊆)≅P,即条件1)对引理2而言是必需的。 定理1有限偏序集P同构于一个拟阵的独立集族所构成的偏序集当且仅当P满足引理2中的条件1)— 4)。 证明:由引理1、2容易得到所需结论。定理1证毕。 一个拟阵的结构并不能够由其独立集的偏序集完全定义。对于不同构的2个拟阵,它们的独立集的偏序集可同构。如令M1=({1,2},T(M1)={∅,{1}})而M2=({1},T(M2)={∅,{1}}),可得(T (M1),⊆)=(T (M2),⊆)而M1M2。原因是M1中有环。事实上,{2}是M1的环,而M2是无环的。 无环拟阵的重要性体现在定理2中。 定理2有限偏序集P与以P为原子集的拟阵M(P)之间的对应是满足引理2中的条件1)— 4)的有限偏序集构成的集合与无环拟阵构成的集合之间的双射。 证明:若P为满足引理2中的条件1)— 4)的偏序集,则由引理2,可知M(P)为无环的拟阵,并且在同构意义下P (M(P))是P。反之,如果对于无环的拟阵M,P (M)是其独立集族,那么利用在引理2中M(P (M))的构造和P (M)的结构,可以导出M(P (M))≅M。定理2证毕。 根据定理2,对于无环的拟阵的研究即为对满足引理2中的条件1)— 4)的有限偏序集的研究。如果重点研究无环的拟阵,那么拟阵中许多有趣问题可以在偏序集中延续。此外,在同构意义下,无环拟阵可以由满足引理2中的条件1)— 4)的偏序集将其特征化。 根据引理1、2,再结合定理2,可以得到简单拟阵的一个重要结果。 推论1由Boolean格P到以P为原子集的拟阵M(P)上的映射是有限Boolean格集合与拥有唯一基的简单拟阵集合之间的双射。 将拟阵的一些结果转化到偏序集的框架下的内容是很有必要的。 定理3若M=(S,T )为拟阵,k∈且0≤k,Tk={X∶X∈T,|X|≤k},那么(S,Tk)为拟阵。 反之,令M2=(S2,T2)为拟阵。若S3=S2∪{b}且T3=T2成立,则M3=(S3,T3)为拟阵并且{b}是该拟阵的环。在下面的证明中仅需要考虑无环的拟阵。 令M无环。由定理2可确定偏序集P (M)即(T,⊆)是对应于M的。根据性质1中的1)— 4)和引理1中的1)— 4)可知,P (M)以S为原子集并且满足引理2中的条件1)— 4)。 令h为P (M)的高函数,并且对x∈P (M)有Xx={a∈P (M)∶a≤x且a∈S}。由引理2中的2)可知x=∨Xx。 令P (M)k={x∈P (M)∶h(x)≤k}。根据引理1的2),可知P (M)k={x∈P (M)∶ρ(x)≤k}= {x∈P ∶|x|≤k},因此P (M)k=Tk成立。 下面证明P (M)k满足引理2中的条件1)— 4)。 容易得知P (M)k满足引理2中的条件1)和4)。 若b∈Max[P (M)k],则a∈Max[P (M)]满足b≤a。在P(M)中,由引理2中的条件3),可以得到[0,a]是Boolean格并且满足[0,a]≅(2{y∈S ∶y≤a},⊆),即[0,b]为Boolean格且[0,b]≅(2{y∈S ∶y≤b},⊆),从而在P(M)k的区间[0,b]k表现在P(M)中是区间[0,b],因此,[0,b]k为Boolean格并且[0,b]k≅(2{y∈S ∶ y≤b},⊆),即对于P(M)k,引理2中的条件3)是成立的。 根据定理1、2,可以得到M(P(M)k)≅(S,Tk)。即(S,Tk)为拟阵。定理3证毕。 定理3与文献[18]中定理1的结果是相同的,但是得到结果的方法不同。这表明本文中的方法是成功的。 文献[20]中的定理2只有简单拟阵才能够满足,但是本文中的定理2对于任何无环的拟阵都适用。因为一个简单拟阵一定是无环的并且无平行元,所以本文中的定理2比文献[20]中定理 2的适用范围广。由此可知,本文中的主要结果即定理2拓广了拟阵已有的结果。事实上,本文中的思想不仅可用于拟阵的其他公理体系结合另外的数学结构,将拟阵特征化,而且也为使更多算法应用于拟阵领域、扩大拟阵的适用范围奠定了理论基础。 在今后的研究中将借助于偏序集理论和贪心算法揭示拟阵更多的性质,并将其应用到更广的范围,例如,利用拟阵和贪心算法寻找概念格的结构。2 偏序集与拟阵的独立集
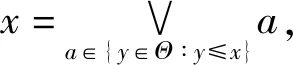

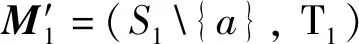
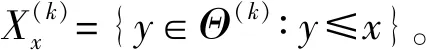
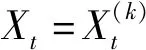
3 总结

