Investigation of the fast magnetosonic wave excited by the Alfvén wave phase mixing by using the Hall-MHD model in inhomogeneous plasma

Zhongzheng LI(李中正),Juanfang HAN(韩娟芳),Fangping WANG(王芳平),Zhengwu CHEN (陈正武) and Wenshan DUAN (段文山),*

1 College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,People’s Republic of China

2 Department of Physics, Gansu Normal College For Nationalities, Hezuo 747000, People’s Republic of China

Abstract The inhomogeneity is introduced by a nonzero density gradient which separates the plasma into two different regions where plasma density are constant.The Alfvén waves, the phase mixing and the fast magnetosonic wave are excited by the boundary condition in inhomogeneous magnetized plasma.By using the Hall-magnetohydrodynamics (MHD) model, it is found that there are Alfvén waves in the homogeneous regions, while the phase mixing appears in the inhomogeneous region.The interesting result is that a fast magnetosonic wave is excited in a different direction which has a nonzero angle between the wave propagation direction and the direction of the background magnetic field.The dependence of the propagation direction of the excited fast magnetosonic wave and its strength of the magnetic field on the plasma parameters are given numerically.The results show that increasing both the driving frequency and the ratio of magnetic pressure to thermal pressure will increase the acceleration of the electrons.The electron acceleration also depends on the inhomogeneity parameters.

Keywords: Hall-MHD, Alfvén wave, phase mixing, numerical simulations, fast magnetosonic wave

1.Introduction

Alfvén wave phase mixing,a possible mechanism for coronal heating,was first proposed by Heyvaerts and Priest[1].It has been studied extensively as a possible mechanism for plasma heating for more than three decades[2-18],Malara et al[2,3]have studied the properties of Alfvén waves propagating in inhomogeneous magnetized plasma.By using a 2.5-dimensional MHD numerical code, they have shown that the interaction between the initial Alfvén wave and the inhomogeneity gives rise to the formation of fast and slow waves.Nakariakov et al [4] have studied the nonlinear excitation of fast magnetosonic waves by Alfvén wave phase mixing.By using a MHD numerical code, they suggest a mechanism of indirect plasma heating by Alfvén wave phase mixing due to nonlinear generation of obliquely propagating fast magnetosonic waves.This work has been further developed for one-dimensional open magnetic configurations with inhomogeneous steady flows by Nakariakov et al [5].Tsiklauri et al [8] have studied the interaction of a weakly nonlinear Alfvénic pulse with inhomogeneous magnetized plasma.By using a MHD numerical code, they found that there is a certain optimal gradient of the inhomogeneity that ensures the maximal efficiency of the fast wave generation.All these studies mentioned above have been performed in the MHD model.However, if the transverse scales in the Alfvén wave drop to lengths comparable or smaller than the proton inertial length, the MHD approximation will be incorrect.

Génot et al [19] studied the interaction of Alfvén wave with inhomogeneous plasmas using self-consistent particlein-cell (PIC) simulations.They found that the Alfvén waves propagating in inhomogeneous plasmas give rise to the formation of a significant electric field.By using PIC simulations, Tsiklauri et al [20-23] have studied the interaction of circularly polarised Alfvén waves with inhomogeneous plasma.They reported the discovery of a new electron acceleration mechanism in which an oblique electrostatic field is generated.Threlfall et al [24] have studied the Hall effect on the damping and phase mixing of Alfvén waves in homogeneous and non-homogeneous equilibrium plasmas.By using hybrid Vlasov-Maxwell, MHD and Hall-MHD simulations, Vásconez and Pezzi et al [25-29] have studied the kinetic Alfvén wave generation by means of compressible MHD and hybrid kinetic numerical simulations.It seems that the plasma dynamics is more complex than that predicted by Moffatt and Parker [30, 31] in the ideal MHD case.

By using a Hall-MHD model, we numerically studied the propagation of the Alfvén waves and the phase mixing in a one-dimensional inhomogeneous magnetized plasma in the present paper.The Alfvén waves, the phase mixing and the fast magnetosonic wave are excited by the boundary condition in inhomogeneous magnetized plasma.The most interesting result found in the present paper is that a fast magnetosonic wave propagating in a direction which is not parallel to the background magnetic field direction is excited.Compared with the previous works which are mainly focused on the Alfvén wave propagating in the direction of the magnetic field, the maximum magnetic field of the fast magnetosonic wave does not appear in the direction of the background magnetic field, but in a direction with a nonzero angle between the direction of the background magnetic field and the propagation direction.Moreover, the maximum magnetic field of the fast magnetosonic wave is larger than that of the Alfvén wave.

This article’s frame is as follows.In section 2, the Hall-MHD model is described.In section 3, the numerical results are given.Finally, in section 4 a summary is given.

2.Hall-MHD model

We now study the propagation of the phase mixing in a onedimensional inhomogeneous magnetized plasma.The plasma dynamics can be described by the Hall-MHD equations as follows [25, 32]:

Figure 1.Initial profiles of ρ(x), B(x) and VA(x), whereVA (x )=B (x ) / ( ρ (x )), h=2 and α=0.1.

where Ee=ρu2/2+P/(γ −1)+B2/(2μ0), W=[Ee+P]u+(1/μ0)E×B, E=−u×B+mi/(μ0ρqe)(∇×B)×B+mi/(ρqe)∇Pe,ρ is the ion mass density,miis the ion mass,u is the ion fluid velocity,B is the magnetic field,qeis the magnitude of the electron charge,P=Pi+Peis the total thermal pressure,Piis the thermal pressure of ions and Peis the thermal pressure of electrons.

The SI units are used in the simulation.However, for the graphical presentation of the results, here we introduce the following normalisation: the distance is normalised tothe time to,the velocity to vA0,the mass density to n0mi,the total thermal pressure to 2n0kBT0, the magnetic fields to B0and the current density to mi/(μ0qevA0) respectively, where n0is the plasma number density at equilibrium state,B0is the background magnetic field,T0is the plasma temperature at equilibrium state,kBis the Boltzmann constant,and γ=5/3 is the ratio of specific heats, ωci=B0qe/miand

We consider a 2.5D configuration where the spatial variables are two-dimensional, but the velocity of the fluid is three-dimensional.The simulation region is 0 ≤x ≤200π and 0 ≤y ≤100π (in dimensionless units).

The boundary condition is as follows:the outflow boundary condition is used at x=0, x=200π and y=100π, while the boundary condition at y=0 is ux(x, 0, t)=, where the parameter ε determines the amplitude of the initial perturbation and ω is the driving frequency.The boundary condition at y=0 actually excites the Alfvén waves.

The initial condition is as follows: we assume that the plasma is inhomogeneous in the x direction.The initial condition of the normalised ion mass density ρ(x) is

Figure 2.ρ(a),T(b),Jy(c),ux(d),uy(e),uz(f),Bx(g),By(h),Bz(i),plotted as functions of x and y at the time t=271.2 for the low-amplitude Hall-MHD simulation, where ω=0.125, β=0.01 and ε=0.05.

where h and α are positive constants.h represents the density difference between two homogeneous regions,while α stands for the width of the inhomogeneous region.The initial magnetic field is in the y direction, and the normalised magnetic field B(x) is determined by the following equation

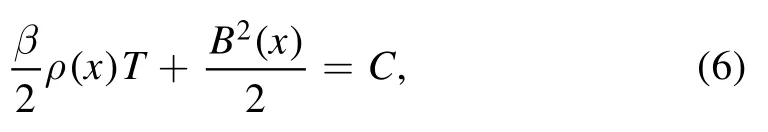
whereFigure 1 shows the initial profiles of ρ(x), B(x) and VA(x).It is noted that there is inhomogeneity which separates the plasma into two regions.The Alfvén wave velocities in both regions are different.The normalised temperature is T=1 and the ion fluid velocity is u=0.

3.Numerical results

Equations (1)-(4) are solved numerically by using USim developed by Tech-X Corporation [33-35].The number of grid cell is Nx=1000 and Ny=500.Numerical parameters in the simulations are as follows: n0=2.5×1017m−3, mi=1.667×10−27kg, B0=118.0×10−4T and T0=1.0×106K.

Figure 2 shows the contour plots of several quantities of ρ, T, Jy, ux, uy, uz, Bx, Byand Bzat the time t=271.2.It is observed that some waves are generated by the boundary perturbation approximately in the y direction.

To get more insight into the features of the excited waves, the time evolution of quantities of ρ, ux,uy, uz, Bx, Byand Bzat x=150π is shown in figure 3.It is noted from figure 3 that ρ,uyand Byare almost all constants,while ux,uz,Bxand Bzare waves with certain period.It is found that the excited waves in the two homogeneous regions satisfy the definition of the Alfvén wave,i.e.,its propagation direction is in the direction of the external magnetic field, the dispersion relation of the excited wave is same as that of the Alfvén wave.Therefore, the excited waves in the two homogeneous regions are Alfvén waves.

It seems from figure 2 that the propagation velocities of the waves in two different regions of both left and the right are different.It is found that VAL=1.0,kL=0.1238,VAR=0.661,kR=0.1881,ω=0.125,which are in good agreement with the analytical result of ω/k=VA(1+k/16) [36], where VALand VARrepresent the velocities of the waves in left and right regions respectively, while kLand kRstand for the wave number of the waves in left and right regions respectively.Therefore,it is inferred that the Alfvén wave is excited by the boundary excitation approximately in the y direction.

Though it is found that there are only Alfvén waves in either the left region or right region,it seems that the wave is more complex at the middle region.Notice that the phase mixing appears in the middle region since the Alfvén wave velocities in both left and right regions are different.It seems from figure 2 that there appears a phase mixing in the y direction,as well as another wave in the direction which has a nonzero angle between the y direction and the wave propagation direction, leading to the maximum magnetic field.Furthermore, the maximum magnetic field in the y direction is larger than that in the phase mixing region.For simplicity, we define an angle θ between the propagating direction of this wave and the direction of the y direction.

Figure 3.Evolution (left column: t=101.7 and right column: t=203.4) of ρ, ux, uy, uz, Bx, By and Bz on the line x=150π.

To gain more insight into the waves in the middle region,the time evolution of the quantities of ρ,ux,uy,uz,Bx,Byand Bzin the regimex=tanθy+100πis shown in figure 4.Noticing that there are obvious wave perturbations of the quantities of ρ, uyand By.Therefore, it seems that there is a wave in the directionx=tanθy+100π.To understand what kind of wave is excited in this direction,figure 5 shows the power spectral density (PSD) of By.It is noted that the frequency of wave is ω=0.127, the wave number is k=0.153,and thus the phase velocity of the wave is 0.83.As a result, it seems that a fast magnetosonic wave is excited in the direction ofx=tanθy+100π.

As a result shown by figure 1 numerically, two different Alfvén waves propagating in the background magnetic field direction are excited in both left and right regions,at the same time, a phase mixing appears in the region which separates both the left and right regions.It is interesting that a fast magnetosonic wave is excited in the direction ofx=tanθy+100π.This fast magnetosonic wave is a novel result reported in the present paper.

In order to get more insight into this fast magnetosonic wave in the directionx=tanθy+100π, dependence of the angle θ,∣By∣maxand∣Bz∣maxon the system parameters of α,h,ω and β is given in figure 6 to figure 9.

Figure 6 shows the dependence of the angle θ,∣By∣maxand∣Bz∣maxon inhomogeneity width parameter α.It indicates that the angle θ increases as α increases.The magnitudes of magnetic fields of both∣By∣maxand∣Bz∣maxreach their maximum value at the point of α=0.1.

Figure 4.Evolution(left column:t=101.7 and right column:t=203.4)of ρ,ux,uy,uz,Bx,By and Bz on the line x=tan θy +100π ,where θ=21.03°.

Figure 7 shows the dependence of the angle θ,∣By∣maxand∣Bz∣maxon the difference of the ion density between two regions h.It seems that the angle θ increases as h increases.The magnitudes of magnetic fields of∣By∣maxreach its maximum value at the point of h=2.5, while∣Bz∣maxincreases as h increases.It indicates that the maximum magnetic field reached at certain inhomogeneity of the middle region.

Figure 8 shows the dependence of the angle θ,∣By∣maxand∣Bz∣maxon the driving frequency ω.It seems that the angle θ decreases as ω increases.The magnitudes of magnetic fields of∣By∣maxand∣Bz∣maxincrease as ω increases.It indicates that the maximum magnetic field increases as the driving frequency increases.

Figure 9 shows the dependence of the angle θ,∣By∣maxand∣Bz∣maxon the plasma parameter β.It seems that the angle θ is almost independent of β.The magnitudes of magnetic fields of∣By∣maxand∣Bz∣maxincrease as β increases.It indicates that the maximum magnetic field increases as the thermal pressure of plasma increases.

It is noted from figure 2(c) that the electric currents are generated due to electric field in the direction of the background magnetic field and it can accelerate plasma particles along the field line.The Alfvén wave phase mixing which will excite the electric field is related to the inhomogeneity of the middle region.In order to get more insight into this timevarying electric currents(electric field),dependence of∣Ey∣maxon the parameters of α, h, ω and β is given in figure 10.The electric fields Eymay accelerate electrons in the direction parallel to magnetic field.Noticing from figure 10 that the maximum electric field (∣Ey∣max) increases as both β and ω increase.It also indicates that∣Ey∣maxreaches its maximum value about h=2.5 and α=0.1.Then it is inferred that in order to accelerate electrons in the direction parallel to magnetic field, we can increase both the driving frequency and the ratio of magnetic pressure to thermal pressure, while choosing certain values of both inhomogeneity parameters such as h=2.5 and α=0.1 for the given parameters in the present system.

Figure 5.(a)Time evolution of By at the point(111.4π,30π)which is on the line x=tan θy +100π .(b)A corresponding FFT spectrum of By in figure 5(a).(c) Spatial evolution of By on the linex=tan θy+100π at t=203.4.(d) A corresponding FFT spectrum of By in fgiure 5(c).

Figure 6.Dependence of(a)θ,(b) ∣B y∣ m ax and(c) ∣B z ∣m ax on the parameter α at the time t=271.2.The other parameters are the same as that in fgiure 2.

Figure 7.Dependence of(a)θ,(b) ∣B y∣ m ax and(c) ∣B z ∣m ax on the parameter h at the time t=271.2.The other parameters are the same as that in fgiure 2.

4.Conclusions

Figure 8.Dependence of(a)θ,(b) ∣B y ∣m ax and(c) ∣B z ∣m ax on the parameter ω at the time t=271.2.The other parameters are the same as that in fgiure 2.

Figure 9.Dependence of(a)θ,(b) ∣B y∣ m ax and(c) ∣B z ∣m ax on the parameter β at the time t=271.2.The other parameters are the same as that in fgiure 2.

Figure 10.Dependence of ∣E y∣ m ax on the parameters of α,h,ω and β at the time t=271.2.The other parameters in the simulations are the same as that in figure 2.

In this paper we have numerically studied the Alfvén waves and the phase mixing in inhomogeneous magnetized plasma by using Hall-MHD model.It is found that there are only Alfvén waves in two different homogeneous regions, while the phase mixing appearing in the inhomogeneous region is due to the difference of the Alfvén wave speed in both homogeneous regions.Furthermore, it is found that a fast magnetosonic wave is excited in a different direction which has a nonzero angle between the wave propagation direction and the background magnetic field direction.The maximum magnetic field of the fast magnetosonic wave is even larger than that in the phase mixing region.The dependence of the propagation direction of the excited fast magnetosonic wave and its strength of the magnetic field on the plasma parameters such as the inhomogeneity between the two regions,the ratio of magnetic pressure to thermal pressure and the driving frequency is given numerically.The results show that in order to accelerate electrons we should increase both the driving frequency and the ratio of magnetic pressure to thermal pressure, while choosing certain values of inhomogeneity parameters in the direction parallel to magnetic field.

Acknowledgments

This research was supported by National Natural Science Foundation of China (Nos.11 965 019, 42 004 131 and 61 863 032).