对象诱导的对偶背景的概念格研究

钱婷，赵思雨

（1.西安石油大学 理学院，陕西西安 710065；2.咸阳师范学院 数学与信息科学学院，陕西咸阳 712000）

为了增进格理论专家与格理论潜在应用者之间的交流，德国数学家Wille于1982年结合哲学中概念及其层次结构的定义，提出了形式概念分析理论[1]。形式概念分析从提出至今已经有三十多年的历史。结合信息时代的特点以及不同理论相结合、相融合的研究理念、再加上形式概念的特殊性及其语义使得自身有诸多有意义的问题有待研究。另外，形式概念分析通过内涵和外延的依赖关系及概念的层次关系直观简洁地反映了隐藏在数据集中的信息，所以近年来它在中医药成分分析[2]，专家系统[3]，数据挖掘以及软件工程[4]等领域得到了广泛的应用，已经成为数据分析和知识发现的有效工具。

形式概念分析与其他理论相结合，也相继产生了不同的概念格模型，而对该模型进一步研究也随之变成了值得深思的问题。姚一豫提出三支决策理论的统一框架描述之后，三支决策理论在决策问题上产生了很好的现实意义[5]。祁建军等结合三支决策与形式概念分析理论提出三支概念分析理论，此理论基本研究对象包括由对象导出的三支概念格和由属性导出的三支概念格[6-7]。这一理论的提出，引起了国内外学者的广泛研究[8-11]。三支概念格的构造理论也被研究[10-11]，通过分析三支概念格的构造理论以及概念格的构造理论，发现同一个形式背景的三支概念格的结构比概念格的结构复杂得多。而事实上，概念格的构造理论已研究得比较成熟[12-14]。如果直接能从形式背景上判断出概念格与三支概念格之间的关系，尤其是同构关系，那么就可以直接利用概念格理论研究三支概念格的相关理论。利用形式背景的属性特征研究概念的理论较多[15-16]，智慧来等基于必然属性给出了概念格中的粒描述[15]。基于此，本文主要通过研究形式背景中对象的特征，讨论概念格、补背景的概念格及AE-概念格之间的关系。

1 基础知识

1.1 形式概念分析

定义1[17]称(G，M，I)为一个形式背景，其中G={g1，…，gp}为对象集，每个gi(i≤p)称为一个对象;M={m1，…，mq}为属性集，每个mj(j≤q)称为一个属性；I为G和M之间的二元关系，I⊆G×M。若(g，m)⊆I，则表示对象g拥有属性m，也记为gIm。

在对象子集X⊆G和属性子集A⊆M上定义一对对偶算子为：

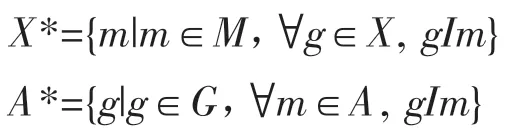
X*表示X中所有对象共同具有的属性集合，A*表示共同具有A中所有属性的对象集合。如果一个二元组(X，A)满足X*=A，且A*=X，则称(X，A)是一个形式概念，简称概念。其中，X称为概念的外延，A称为概念的内涵。

性质1[17]对于形式背景(G，M，I)，可得基本性质(∀X1，X2，X⊆U且∀B1，B2，B⊆A)为：

1）X1⊆X2⇒X*2⊇X*1，B1⊆B2⇒B*2⊇B*1；

2）X⊆X**，B⊆B**；

3）X⊆X***，B⊆B***；

4）X⊆B*⇔B⊆X*；

5）(X1∪X2)*=X*1∩X*2，(B1∪B2)*=B*1∩B*2；

6）(X1∩X2)*⊇X*1∪X*2，(B1∩B2)*⊇B*1∪B*2；

7）(X**，X*)和(B*，B**)都是概念。

用L(G，M，I)表示形式背景(G，M，I)的全体概念，LI(G，M，I)表示形式背景(G，M，I)的全体概念内涵。在偏序关系(X1，A1)≤(X2，A2)⇔X1⊆X2(A1⊇A2)下，可以证明：

L(G，M，I)是格，并且是完备格，称其为形式背景(G，M，I)的概念格（文中称为经典概念格）。

定义2[17]设K1=(G，M，I)，K2=(H，N，J)是两个形式背景。α，β分别是G到H，M到N的双射。若gIm⇔α(g)Jβ(m)，则称K1与K2是同构的。

基于上述定义，有如下结论。

定理1[17]同构的形式背景相应的概念格是同构的。

定义3[17]设(G，M，I)为形式背景，对于任意对象g，h，若g*=h*⇒g=h，且对于任意属性m，n，若m*=n*⇒m=n，则称形式背景(G，M，I)为净化形式背景。

本文中，净化形式背景只是指对象是净化的，即：设(G，M，I)为形式背景，对于任意对象g，h，若 g*=h*⇒g=h，则称形式背景(G，M，I)为净化形式背景。

1.2 三支概念格

结合形式概念分析与三支决策的思想，祁建军等首先提出了三支概念分析[6-7]。与形式概念分析不同的是，三支概念分析不仅考虑原背景上“共同拥有” 的信息，也进一步考虑了补背景上“共同不拥有”的信息。且针对“共同不拥有”的信息，祁建军等提出如下算子。

定义4[6-7]设(G，M，I)是一个形式背景，X⊆G，xIca}。

相对于该负算子，祁建军等称原背景上的*算子为正算子，并将形式背景的正算子与负算子相结合，给出了属性导出的三支算子的定义与性质[6-7]。

定义5[6-7]设(G，M，I)是一个形式背景，X，Y⊆G，A，B⊆M，一对由对象导出的三支算子定

在属性导出的三支算子的定义下，祁建军等给出了AE-概念与AE-概念格的定义。

定义6[6-7]设(G，M，I)是一个形式背景，X，Y⊆G，A⊆M。若A◁=(Z，Y)且(x，y)▷=A，则称((X，Y)，A)为由属性导出的三支概念，简称AE-概念。其中(X，Y)为((X，Y)，A)的外延，A叫作AE-概念的内涵。

记所有AE-概念内涵构成的集合为AELI(G，M，I)，并记所有AE-概念构成的集合为AEL(G，M，I)，并且在偏序关系((X，Y)，A)≤((Z，W)，B)⇔(X，Y)⊆(Z，W)⇔B⊆A下，AEL(G，M，I)是完备格。

2 对象诱导的对偶背景及其概念格

研究形式背景(G，M，I)具有的特征，讨论AEL(G，M，I)与L(G，M，I)之间的关系，首先赋予对象以下特征。

定义7设(G，M，I)为形式背景，g∈G。若存在h∈G，有g*∩h*=Ø且g*∪h*=G，则称h为g的对偶对象。

通过上述定义，很容易得到以下性质。

性质2设(G，M，I)为形式背景，g，h，t∈G，有以下结论成立：

1）若h为g的对偶对象，则g也为h的对偶对象；

2）若h，t均为g的对偶对象，则h*=t*。

例1设(G，M，I)为形式背景，G={1，2，3，4，5}，M={a，b，c}，I关系如表1所示。

表1 形式背景(G,M,I)

由定义6知，对象1与对象4，5是对偶对象。

定义8设(G,M,I)为形式背景，若对于任意g∈G，都存在对偶对象，则称(G，M，I)为对象诱导的对偶背景。

例2（续例1）形式背景(G,M,I)如表1所示，由定义6知，1的对偶对象为4、5，2的对偶对象为3，3的对偶对象为2，4的对偶对象为1，5的对偶对象为1，故由定义7知，表1所示的形式背景为对象诱导的对偶背景。

定理2若(G，M，I)为净化的对象诱导的对偶背景，则|G|为偶数。

证明：因为(G，M，I)为对象诱导的对偶背景，所以对于任意的g∈G都存在对偶对象，证对偶对象唯一。若h，t均为g的对偶属性，显然h*=t*，又由于(G，M，I)为净化背景，从而h=t。显然对于任意的g∈G，有且仅有一个对偶对象，从而对象成对存在，故|G|为偶数。

定理3若(G,M,I)为净化的对象诱导的对偶背景，则(G，M，I)≅(G，M，IC)且L(G，M，I)≅L(G，M，IC)，其中IC=G×MI。

证明：定义α：G→G，对于任意g∈G，α(g)=β：M→M，对于任意m∈M，β(m)=m，其中为g的对偶对象。由于(G，M，I)为净化的对偶背景，所以由定理1知，对于任意g∈G，存在且唯一，所以α也为双射，显然β为双射。

若gIm，则m∈g*。由于为g的对偶对象，所以g*∪=M且g*∩=Ø。从而由于

研究L(G，M，I)与L(G，M，IC)中元素的具体关系。

定理4若(G，M，I)为净化的对偶背景，则LI(G，M，I)=LI(G，M，IC)。

证明：由定理3知，L(G，M，I)≅L(G，M，IC)，且通过证明过程知，若g与为对偶对象，则

定理5若(G，M，I)为净化的对偶背景，则(X，A)∈L(G，M，I)⇔(ˆ，A)∈L(G，M，IC)，其中为g的对偶对象，g∈X}。

证明：简记为g的对偶对象，g∈X}为若(X，A)∈L(G，M，I)，由定理4的证明知显再利用反证法证明假设不成立，则存在即但t∉X，其中t是的对偶对象。又由定理4的证明知，则故但t∉X矛盾，从而

另外，由定义5知，三支算子是由正负算子所决定的。而对于净化的对偶背景，正负算子所决定的概念格是同构的，那么由三支算子所决定的三支概念格与他们之间的关系由以下定理给出。

定理6若(G，M，I)为净化的对偶背景，则LI(G,M,I)=AELI(G，M，I)并且L(G，M，I)≅AEL(G，M，I)。

证明：任取(X，A)∈L(G，M，I)，由概念的定义知X*=A。根据算子的性质知从而由AE-概念的定义知又(X，A)的任意性知LI(G，M，I)∈AELI(G，M，I)。

下证AELI(G，M，I)⊆LI(G，M，I)。

任取((X，Y)，A)∈AEL(G，M，I)，由三支概念的定义知，由于LI(G，M，I)=LI(G，M，IC)，故从而又由于内涵具有保交性，所以即A∈LI(G，M，I)，从而AELI(G,M,I)⊆LI(G，M，I)。

综上，LI(G，M，I)=AELI(G,M,I)。

定义a：L(G，M，I)→AEL(G,M,I)，对于任意显然a是一个双射。若(X1，A1)≤(X2，A2)，则A1⊇A2。又由a的定义知因为A1⊇A2，所以即a(X1，A1)≤a(X2，A2)，反之也成立。从而a是L(G，M，I)到AEL(G,M,I)的序同构，即L(G，M，I)≅AEL(G，M，I)。

通过例子净化的对象诱导的对偶背景的概念格、补背景的概念格以及AE-概念格。

例3（续例1）将表1中形式背景净化，得净化形式背景如表2所示。

表2 表1的净化形式背景(G’,M,I)

例4（续例3）表2的概念格，补背景概念格，AE-概念格分别如图1、图2、图3所示。

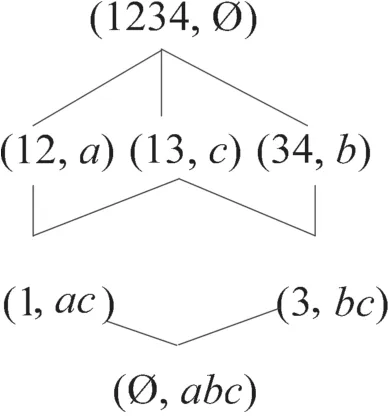
图1 L(G’,M,I)

图2 L(G’,M,IC)

图3 AEL(G’,M,I)

若(G，M，I)不是净化的对象诱导的对偶背景，L(G，M，I)与AEL(G，M，I)是否还会同构，事实上，这里的净化条件是多余的。若(G，M，I)是对象诱导的对偶背景但不是净化背景，则对于g∈G，存在多个对偶对象，假设存在两个对偶对象h，t，可知h*=t*，根据约简的性质知，在构造格时，t或者h可以看成看作可约对象，进而可将原形式背景化为净化的对象诱导的对偶背景。由此可以将上述定理推广至如下结论。

定理7若(G，M，I)为对象诱导的对偶背景，则L(G，M，I)≅L(G，M，IC)且L(G，M，I)≅AEL(G，M，I)。

根据上述几个结论，研究AE-概念格的构造方法。

根据定理6的证明，很容易得到利用概念格构造AEL(G，M，I)的方法，如下述定理所述。

定理8若(G，M，I)为对象诱导的对偶背景，

定理8 与定理5结合，可以得到利用概念格与补背景的概念格AE-概念格一种方法，如下所示。

推论1若(G，M，I)为对象诱导的对偶背景，

则AEL(G，M，I)={((X，Y)，A)|(X，A)∈L(G，M，I)且(Y，A)∈(G，M，IC)}。

3 结语

目前形式概念分析及三支概念分析均已发展成为数据分析和知识发现的有效工具。本文主要通过研究形式背景的对象特征，讨论了概念格、补背景的概念格及AE-概念格三者在概念内涵、概念以及格结构上的关系。具体地，证明了在对象诱导的对偶背景下，AE-概念格、概念格及补背景的概念格是同构的。最后还给出了AE-概念格的两种构造方法。本文讨论的是一种简单的形式背景。事实上，值得进一步思考的是若对于某一对象g∈G，不存在对偶对象，三者具有的关系，以及进一步研究AE-概念格与概念格同构的必要条件。