基于Logit模型的游戏互动法教学效果实证研究
房琳,王怡
(商洛学院 经济管理学院,陕西商洛 726000)
游戏教学法是游戏和教学的结合体。游戏是指在某一固定时空范围内进行的一种活动,参与者自愿接受其有绝对约束力的规则。它具有自由性、开放性和体验性,就游戏的内在精神而言,教学可以成为游戏[1]。德国哲学家康德最早对游戏教学法进行系统阐述,世界许多知名大学将管理游戏引入课程教学[2-3]。国内一些学者从不同理论角度探讨游戏教学法的可操作性与实施原则[4-5],基于游戏化学习理念进行翻转课堂设计[6];另一些学者从实践角度,将游戏教学法应用到历史、管理学、现代教育技术等诸多课程中[7-9]。博弈思想起源于游戏,博弈论是研究策略性决策行为的社会经济科学分支[10],其课程内容多分析人际互动行为,博弈方之间的相互依存和互动是游戏的一个特征[11],从内容角度看比较适用游戏教学法。董申等介绍了游戏化多角色博弈商业模拟的教学设计思想[12];房琳等[13]提出将游戏互动教学法引入博弈论课堂,给出了基本教学过程和游戏设置原则。但实施游戏互动教学是否能够促进课堂教学效果,游戏教学法的实施效果会受到哪些因素的影响,并没有学者进行深入的实证研究。基于此,本研究在博弈论课堂实施游戏教学的基础上,提出理论假设:游戏互动教学法对博弈论课程教学有较为明显的促进作用。借鉴已有研究对教学效果的实证分析[14-16],采用实验对照方法收集数据,建立多分类有序变量的累积Logit 计量模型,验证分析游戏互动法在教学实施中的实施效果和影响因素。
1 研究对象与方法
在A、B 两个平行班开设博弈论的公共选修课程,教学中结合课程内容设置不同的教学游戏。为验证教学效果的理论假设,将其中两个游戏进行实验,设计课堂测试收集数据,把握学生对相应知识点的掌握情况,并进行后续分析。具体游戏及设计:首堂课设计“字母二选一”游戏[13],帮助学生掌握博弈模型的五个基本要素(博弈方、信息、策略、次序、收益)以及得益矩阵的写法,后称游戏一。纳什均衡是博弈理论的一个重要概念,也是一个难点知识,为帮助学生理解,讲解该知识点时,设计“选数字”游戏(2 人一组,独立选择并写出1~10 中的5 个数字,两人所选数字无重复的小组,则成功),帮助学生深入理解均衡概念,掌握纳什均衡的多重性,后称游戏二。
为研究实施游戏教学的教学效果与影响教学效果的因素,游戏一为A、B 两班都进行;游戏二只在A 班进行,为实验组;B 班不进行,为对照组。抽样调查时,A 班发放问卷118 份,回收有效问卷109 份;B 班随机发放问卷70 份,回收有效问卷67 份。
2 游戏教学法实施效果分析
根据游戏二的教学对比实验,分析游戏教学法的实施效果。问卷中设计对“均衡”理解判断的选择题1 题,概念描述的填空题1 题。以“知识点的掌握程度”反映游戏教学法的实施效果。问卷整理过程中,两个题目均答对判定为“掌握均衡概念”,认为游戏教学法有效;否则判定为“未完全掌握均衡概念”,认为游戏教学法无效。
2.1 游戏教学法实施效果对比试验的样本描述
实验组(A 班 109 份样本)和对照组(B 班 67份样本)数据整理分析如表1和表2。

表1 游戏实施对知识点掌握的影响

表2 游戏实施对知识点掌握的影响程度分析
表1展示了游戏二课堂实施实验结果的原始数据及区间估计结果。可以看到,游戏实施的实验组,对“均衡”概念的知识掌握比例为39.4%,在95%置信度下,该组知识点掌握比例的置信区间为[0.3,0.49],远高于未实施游戏的实验组掌握比例。这说明,游戏互动教学的实施可以促进学生对知识点的掌握和理解。(说明:“两题均答对”才能判定为知识点掌握,判定标准严格,这里的知识点掌握率不理想。)
表2计算了游戏实施与否对知识点掌握比例影响的程度。可以看到,实施游戏组对知识掌握的比例是未实施游戏组的2.17 倍(相对知识掌握率RR=0.39/0.18=2.17);相对于未实施游戏组,实施游戏教学学生组的知识掌握发生比率是前者的2.9 倍(知识掌握比率比OR=0.639/0.22=2.9)。
从样本数据来看,在博弈论课程中使用游戏教学法,很大程度提高了学生对难点知识的掌握率。可以认为,游戏教学法在博弈论课程中实施的效果较好。为验证结论,对游戏教学法的实验教学进行统计推断。
2.2 游戏教学法实施效果对比试验的推断分析
2.2.1 提出假设
原假设H0:知识掌握程度与实施游戏教学无关。备择假设H1:知识掌握程度与实施游戏教学有关(即实施游戏教学可帮助掌握知识点)。
2.2.2 计算检验统计量
对表1所示的2×2 列联表进行χ2检验。首先构建χ2检验的理论频数表,如表3。

表3 游戏实施对知识点掌握比例的理论频数
其中,Aij表示原始资料数值,Tij表示原始数据资料的理论频数,由计算可得,n 为总样本数,ni表示第i 行合计值,mj表示第j 列合计值。
2.2.3 统计推断
2×2 列联表的 χ2自由度为 1。在 0.05 显著性水平下,得到临界值 χ20.05,1=3.84。由于 χ2>χ20.05,1,P<0.05,拒绝 H0,接受 H1。
从推断分析结果来看,在统计学意义上,在博弈论课堂教学中,学生对难点知识的掌握程度与游戏互动教学的实施有关,可认为实施游戏教学可以帮助学生理解和掌握知识点。该教学方法的引入有一定的实际意义。这与样本数据的分析结果一致,也与学生的课堂表现相符。
3 游戏教学法实施效果的影响因素
3.1 变量设置
考虑课程性质和难度,结合课堂具体情况,认为可能会影响互动游戏实施效果的因素有性别、学科、游戏参与程度、对游戏本身的感兴趣程度、学生对课堂游戏的接受程度等。问卷主要从这几个方面设计问题,度量游戏实施效果的影响因素。
设 x1表示“性别”,取值“女/男”;x2表示“学科”,取值“文/理”;x3表示“游戏参与程度”,取值“未参与/参与不积极/积极参与”;x4表示“对游戏本身的感兴趣程度”,取值“无趣/比较有趣/非常有趣”;x5表示“是否接受在大学课堂组织实施游戏”,取值“不接受/可以接受”。
设计问题考查对博弈基本要素(博弈方、信息、策略、次序、收益)的掌握数量,以衡量游戏教学法的实施效果。分别将“掌握3 个及以下/掌握4 个/掌握5 个”确定为知识掌握程度一般/较好/很好。
3.2 游戏教学法实施效果影响因素的样本描述
游戏一在两个班级课堂教学中都使用,因此可以利用全部176 个样本数据进行分析,如表4所示。

表4 游戏实施效果
从表4样本数据汇总中的知识点掌握率来看,性别、学科、游戏参与程度和对游戏的感兴趣程度,均对知识点掌握有影响,即会影响游戏教学法的实施效果。由于“是否接受课堂实施游戏”的数据中,全体样本均选择接受,因此该因素不具备分析条件,则在后续分析中删除变量x5。
其中,相对于女生,男同学对知识掌握的比例略高(男同学知识点掌握很好的比例35%,高于女生的比例29%);理科学生比文科学生的知识掌握程度更好(理科学生掌握很好的占38%,高于文科的23%)。样本数据还反映出学生对于游戏的感兴趣程度较高,96%的学生认为游戏有趣;但游戏的参与率有待提升,近30%的学生未参与游戏。从侧面反映出学生的课堂积极性仍然没有被充分调动。
样本的描述统计结论具有一定启发性,但并不能说明变量是否具有统计学意义,为此构建Logit 回归进行进一步分析。
3.3 游戏教学法实施效果影响因素分析模型构建
结合Logit 模型假设,因变量为三分类的有序变量,采用累积Logit 回归模型。设“知识点掌握程度”为因变量Y,是有k 个等级的有序变量,k=3,即 Y1为“知识掌握一般”,Y2为“掌握程度较好”,Y3为“掌握程度很好”。χT=(x1,x2,…,xn)为自变量矩阵。记Pj为等级小于j 的累积概率,由式(1)决定,与式(2)等价。
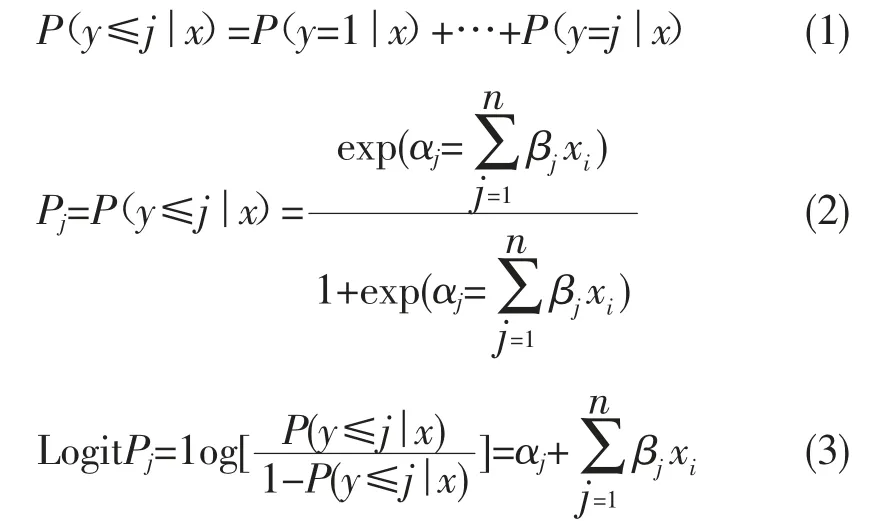
对累积概率做Logit 变换,构造累积Logit 回归模型,如式(3),表示小于或等于类别j 相对于大于类别j 的累积概率的比数之对数,也称为比例比数模型[17]。其本质是通过合并将原来的多分类因变量转变为一般的二分类因变量。该模型的回归系数β 不受j 的调节,可解释的是其比数比OR=expβj。
3.4 游戏教学法单因素对知识点掌握程度的影响
分别以性别、学科、游戏参与程度、对游戏的感兴趣程度为自变量,以知识掌握程度为因变量进行分析。利用Stata 14 对数据进行运算和分析,似然比统计量检验见表5。从单因素回归的结果来看,其中三个自变量对理论知识点掌握均有影响。

表5 游戏教学法单因素影响似然比统计量检验
由表5可见,性别对教学效果的影响不显著,基本符合样本描述结果。学科对教学效果的影响显著,符合样本描述结果。由于博弈论属于交叉学科,需要一定的经济学知识和数学基础,对逻辑推理能力有要求,对于部分数理基础薄弱的文科学生而言,学习有一定的难度。尤其是理论知识难点,一味采取传统理论讲授的方法,教学差异比较明显。该结果基本符合教学经验。在游戏互动教学环节,游戏参与程度越高,对游戏越感兴趣,知识点的掌握就越好,即游戏教学效果越好。这些结论与样本描述结果一致,也符合设计游戏教学方法的初衷。
3.5 游戏教学法多因素对知识点掌握程度的综合影响
进一步考虑在游戏教学法使用中,4 个因素对知识点掌握程度的综合影响,利用Stata14,实施累积Logit 模型的分析结果如表6所示。回归方程自由度为6,卡方检验值为140.59,P 值的概率为0.0000,说明参数整体显著不为0;对数似然比统计量报告为-109.38,模型通过了显著性检验,方程有效。从回归结果中可以看出。
1)实施游戏互动教学后(模型中表现为控制游戏参与程度和对游戏感兴趣程度),学科对知识点掌握程度的显著影响消失。说明在博弈论的课堂教学中,适时使用游戏互动的方法,在一定程度上削弱学科对知识点掌握程度的影响,认为游戏教学法有助于提升课堂教学效果。
2)游戏参与程度越高,对知识点掌握的帮助越大,即游戏实施的效果越好。在控制了性别、学科因素情况下,以未参与游戏的学生为参照分析,积极参与游戏互动的学生与未参与游戏的学生相比,知识点“掌握很好”发生率是“掌握一般”发生率的e4.79=120 倍;参与游戏一般的学生与未参与游戏的学生相比,知识点“掌握很好”发生率是“掌握一般”发生率的e1.84=6.3 倍。简言之,在控制了性别、学科因素的情况下,参与游戏教学的学生知识点“掌握很好”的发生比率至少是未参与游戏学生的6.3 倍。
3)对游戏本身很感兴趣的同学,游戏互动教学对知识点掌握的帮助显著。相对于认为游戏无趣而言,对游戏很感兴趣的同学,知识点“掌握很好”发生率是“掌握一般”发生率的e2.6=13.46倍。

表6 游戏教学法多因素对知识点掌握程度影响的模型参数估计结果
4 结论
本研究是在游戏互动教学法引入博弈论课堂教学,实施较为成熟之后进行的,旨在检验其实施效果。从教学经验和课堂反映来看,学生对游戏教学的接受程度良好。针对课堂中进行的两个游戏,设计问卷收集数据,进行描述和推断统计分析。列联表分析结果表明:实施游戏组对知识掌握的发生比率是未实施游戏组的2.9 倍,通过卡方检验说明学生对难点知识的掌握率与游戏教学的实施有关,即可认为游戏教学法的引入促进了博弈论课堂教学的教学效果,对学生的难点知识掌握率有提升。在游戏教学实施中,游戏的参与程度是决定其教学效果的重要因素:在控制了性别、学科因素情况下,参与游戏教学的学生知识点“掌握很好”的发生比率至少是未参与游戏学生的6.3 倍。决定游戏教学法实施效果的另一个主要因素是学生对游戏本身的感兴趣程度:对游戏很感兴趣的学生与认为游戏无趣的学生相比,知识点“掌握很好”发生率是“掌握一般”发生率的13.46 倍。
本研究中学生对游戏的参与率并不十分理想,在后续的博弈论课程教学中,应更加注重游戏的组织过程,更大程度调动学生的积极性,鼓励学生积极参与到游戏互动中;同时注重游戏的趣味性,多设计趣味性强,容易理解和选择策略的游戏,以期更好的促进教学,提升教学效果。另外,博弈论的理论性质决定了引入课堂的策略游戏会有一定难度,本研究中未充分考虑游戏难度对实施效果的影响,在后续教学中需进一步研究。

