亚微米级颗粒物在气体动压轴承内运动与沉积分析

冯 明，侯 冲，忽敏学，刘志宏

（1.北京科技大学 机械工程学院，北京 100083；2.天津航海仪器研究所，天津 300131）

螺旋槽轴承是气体动压轴承的一种基本形式，因其具有较高的承载能力和良好的稳定性，在气浮陀螺中得到广泛应用[1]。陀螺电机启停次数是评价气浮陀螺的关键指标之一，而引起电机不启动的主要原因是轴承中多余物的堵塞[2]。多余物在气体动压轴承螺旋槽的泵入作用下，进入气膜间隙并沉积在轴承表面，从而增大了轴承摩擦力矩和电机启动难度。多余物主要来源是定子绕组浸渍漆和各种粘合剂挥发的低分子有机物，次要来源是轴承的启停磨损产生的金属颗粒物[3]，但尚不清楚颗粒的大小和密度在不启动问题中所发挥的影响作用。

为提高电机启停可靠性，可采用零组件清洗、热真空除气等技术手段抑制多余物的产生[3]，这些方法虽在实践中取得的一定的效果，但并没有彻底解决污染问题，且由于技术局限，在现阶段乃至今后较长时间内尚不能完全杜绝污染源。因此，寻求合理的轴承结构设计，使进入轴承间隙的多余物快速排出或引导多余物在特定区域沉积，是现阶段提高电机启停性能的有效措施。目前对螺旋槽气体动压轴承基本特性的研究较为深入，但对轴承污染问题的研究较少。

传统的动压轴承计算方法和单相流模型不能分析气体和颗粒物在轴承中运动的问题，需要借助气固两相流模型来解决。目前，气固两相流的分析计算主要应用在冶金、粮食加工、流化床气力输送、旋风分离器和内燃机缸内湍流燃烧模拟等领域[4-7]。本文将其引入到具有狭小间隙的气体轴承研究中，对多余颗粒物在轴承间隙中的运动和沉积规律进行研究，阐述不同直径和密度的颗粒物在运动规律和沉积数量的差异性，并对轴承结构参数进行优化分析，在保证承载力和刚度的前提下，寻求引导多余物排出或弱化多余物沉积的结构方案。

1 模型与求解方法

1.1 理论模型

颗粒物的大小与轴承气膜的径向和周向尺寸相比是高阶小量，因而颗粒相非常稀薄，所以本文采用基于欧拉-拉格朗日法的离散相模型，将气体流场作为连续相，颗粒物作为离散相处理。该模型的优点在于物理概念明确，计算简单，可追踪描述颗粒的复杂运动。计算中只考虑轴承稳定工作的状态，气体流场为定常流动，但颗粒物在轴承中的运动形态和沉积数量会随时间变化，为非定常模式。

对连续相的计算，用流动方程描述欧拉坐标系下流体质量、动量及能量的运输过程，采用气体动压轴承计算中通用的假设[8]：

1）气体流动为粘性可压缩流体的层流；

2）气膜与轴颈和轴瓦无相对滑动；

3）轴瓦与转子面均为理想光滑表面，气膜厚度为常值，不考虑粗糙度的影响；

4）忽略气体流动过程中温度变化，计算温度为300 K。

离散相颗粒则由力平衡微分方程独立控制，在拉格朗日坐标系下考察流体对颗粒作用，采用离散相计算中通用的假设：

1）颗粒物为无粘性规则球形，与气流存在速度及温度滑移；

2）忽略粒子对流体及粒子间的作用，只考虑流体对粒子的影响。

因此本文研究的气体动压轴承的流场计算满足基本流体力学控制方程[9]：

1）连续性方程

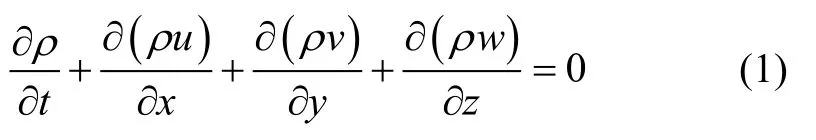
其中，ρ是流体密度，t是时间，u、v、w是速度矢量在x、y、z方向的分量。

2）动量守恒方程

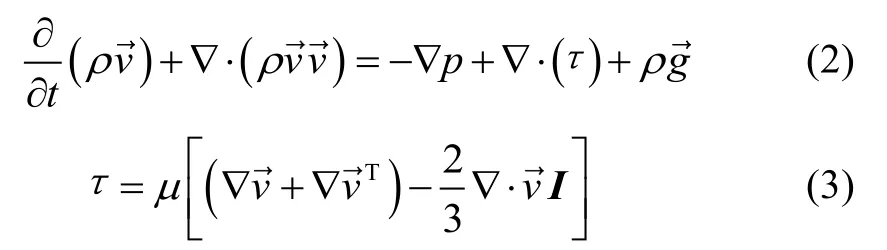
其中，p是流体微元体上的压强，▽是哈密顿算子，τ是因分子粘性作用而产生的作用在微元体表面的应力张量，ρg是单位质量力，μ是流体的粘度，I是单位张量，式(3)右边第二项是体积膨胀的影响。

3）能量守恒方程

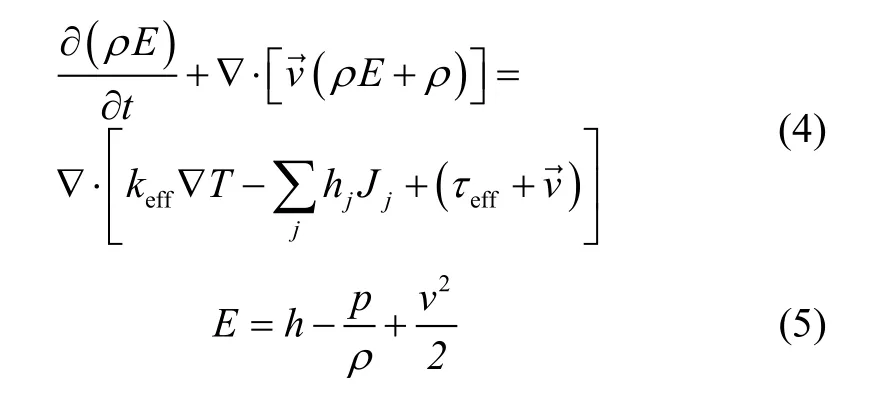
其中，E为流体微团的总能量，T是气总温，h是单位工质的焓，hj为组分j的焓，Jj为组分j的扩散通量，keff为有效热传导系数，τeff是有效力。

4）颗粒的作用力平衡方程

颗粒相计算满足颗粒的力平衡方程（粒子惯性=作用于粒子上其他的力），其在笛卡尔坐标系中可以写成：

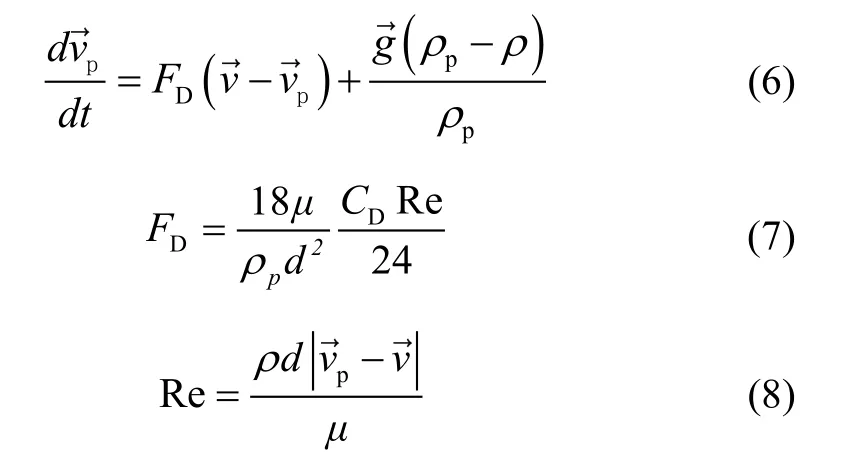
1.2 模型简化

某外转子气体动压陀螺电机结构如图1所示[10]。由转子组件、定子组件、左右止推板和电机轴等组成，采用气体动压轴承作为支撑。将轴承气膜从中分离出来，得到一个由左、右止推轴承和左、右径向轴承组成的联合轴承，如图2所示。若不考虑轴向偏心，该联合轴承左右对称，可取一半建模。颗粒物从止推轴承外圈被吸入，设定吸入时间为1 ms，之后用色标追踪每个被吸入的颗粒物在轴承中的位置，计算显示25 ms后颗粒物的运动趋于稳定，如图3所示。可知，颗粒物几乎只分布于止推轴承的槽区和台区，并没有进入径向轴承，这是由于只有止推轴承的外圈与外界相通，轴承结构对称，气膜流场稳定后，径向轴承内的气体几乎不再与外界发生交换，所以颗粒物不能进入径向轴承。因此对联合轴承内多余颗粒物运动和沉积的研究可简化为对内径封闭的螺旋槽气体动压止推轴承的研究。

螺旋槽止推轴承的气膜间隙模型如图4所示。该模型分为槽区、台区和坝区，轴承中的螺旋槽采用对数螺旋线，其结构参数如表1所示。网格划分采用六面体网格，在间隙方向进行多层细化，生成的网格总数量为139万。

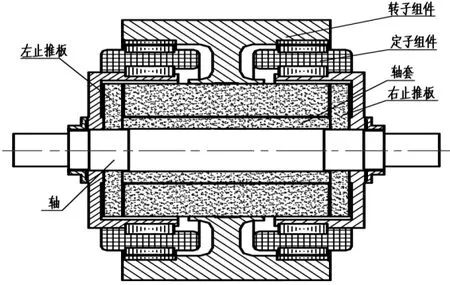
图1 陀螺电机结构示意图Fig.1 Schematic of gyro motor

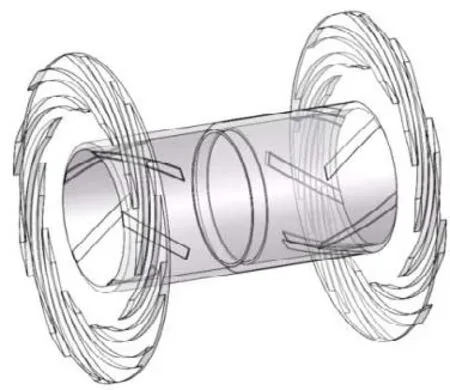
图2 联合轴承气膜结构示意图Fig.2 Clearance of coupled bearing

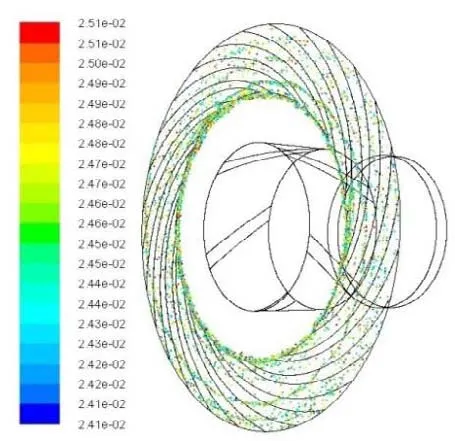
图3 颗粒物沉积分布（t=25 ms）Fig.3 Deposition of particles (t=25 ms)

表1 止推轴承结构几何参数Tab.1 Geometrical parameters of thrust bearing

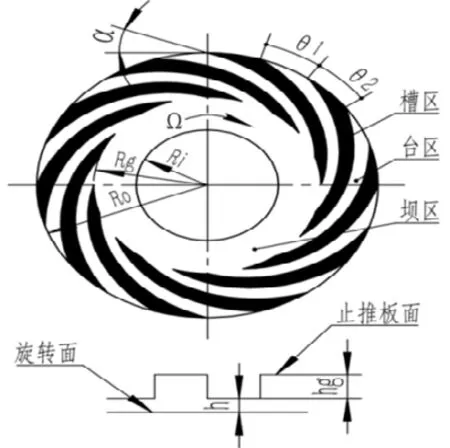
图4 止推轴承气膜结构示意图Fig.4 Schematic diagram of film

1.3 边界条件与计算流程

计算中将止推轴承内圈设置为壁面，轴承外圈为压力入口，转子面转速Ω为30 kr/min。流体介质为空气，考虑可压缩性，将其设置为理想气体。以轴承压力入口为颗粒物面射流源，颗粒的初始速度为 0，质量流量为1g·s-1，释放时间为1 ms。计算中求得收敛且稳定的流场后再释放颗粒物，计算流程如图5所示。

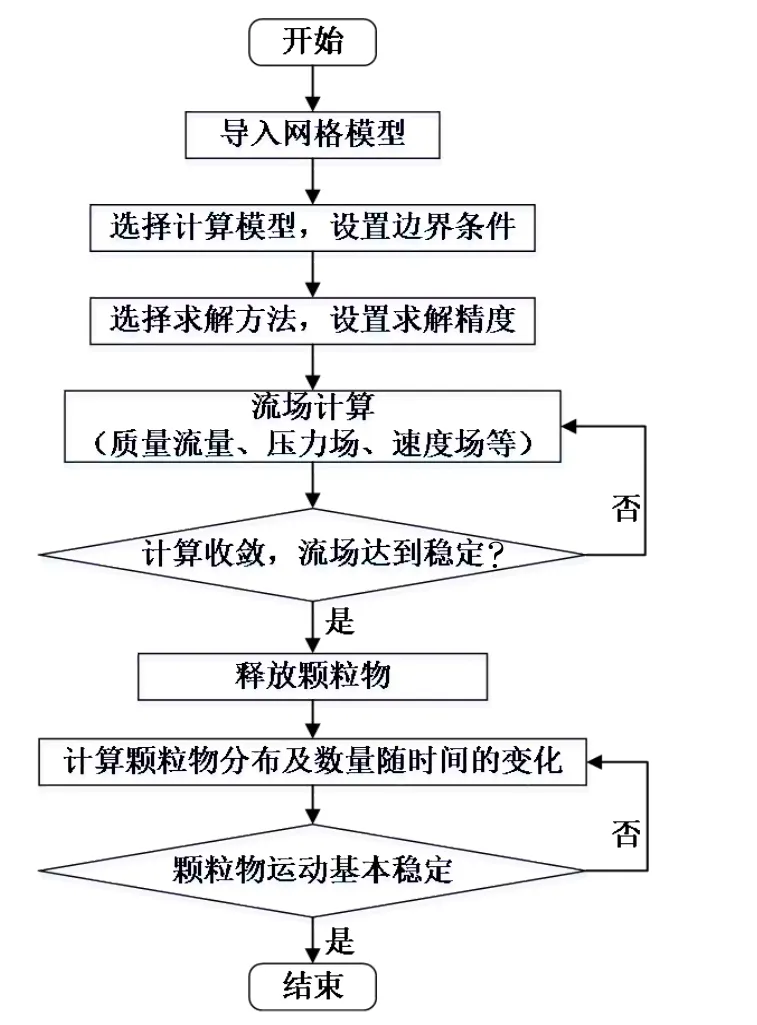
图5 计算流程图Fig.5 Flow chart of calculation

2 计算结果与分析

2.1 计算方法校验

在进行气固两相流计算之前，为了检验模型设置的正确性，对文献[11]中的轴承（N=16，α=18°，Ro=29 mm，Rg=18.25 mm，Ri=14.5 mm，λ=1.57，hg=20 μm，Ω=30 kr/min）进行了仿真计算。轴承承载力的结果比较如图6所示。

由图6可知，本文的计算结果与实验结果比较吻合，间隙24 μm时两结果差别最大，偏差为11%。h=15 μm时轴承气膜的压力分布如图7所示。气膜压力沿螺旋槽由外至内逐渐上升，气体在槽的根部受到坝区的阻挡不断被压缩，压力达到最大值，而后逐渐降低至大气压。在轴承螺旋槽外圈，由于螺旋槽的泵入作用以及气体由台区流入槽区气膜厚度增加导致槽中气体密度减小形成负压。同时每个槽台之间存在阶梯效应，压力成锯齿形分布，符合气体动压螺旋槽轴承的典型分布特征。这说明本文采用的计算方法正确，计算结果可信，为进行气固两相流的计算奠定了基础。

图6 轴承承载力对比图Fig.6 Comparison of loading capacity

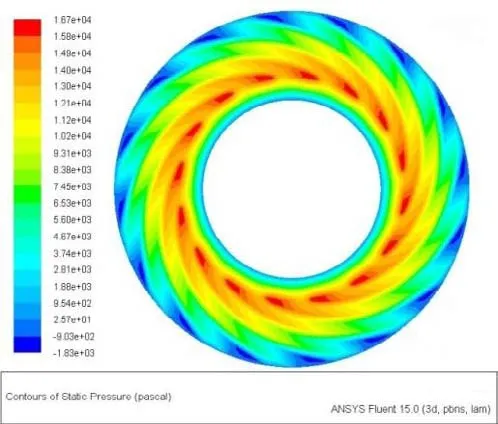
图7 轴承压力云图Fig.7 The pressure distribution

2.2 颗粒物典型运动沉积规律

槽深比γ=4时颗粒物进入轴承后的运动如图8所示。以第一个颗粒物进入轴承为时间原点，释放1 ms后的颗粒数量为进入轴承的颗粒总数量。由图可知，虽然止推轴承的整个外圈都有颗粒物释放，但其只由螺旋槽口进入（图8(a)），之后颗粒物沿槽向中心方向旋进（图8(b)）；颗粒物约在7 ms的时候运动到槽末端，由于槽端壁面的阻挡而向间隙方向运动（图8(c)），然后在离心力及气流作用力下螺旋运动，约在10 ms时开始被甩出轴承(图8(d)）；15 ms时颗粒物已明显减少(图8(e)），25 ms时颗粒分布及数量基本稳定，此时颗粒物主要沉积在螺旋槽端部和槽中（图8(f)）。

槽深比γ=1时颗粒物进入轴承后的运动如图9所示。与γ=4时的运动不同，这时颗粒物不再只沿槽进入轴承，台区也有颗粒物被进入（图9(a)），且颗粒物大多不能运动到槽端，进入轴承后便沉积在靠近入口的圆周面处（图9(b)、9(c)），25 ms时的分布与刚进入轴承时差别不大（图9(d)）。

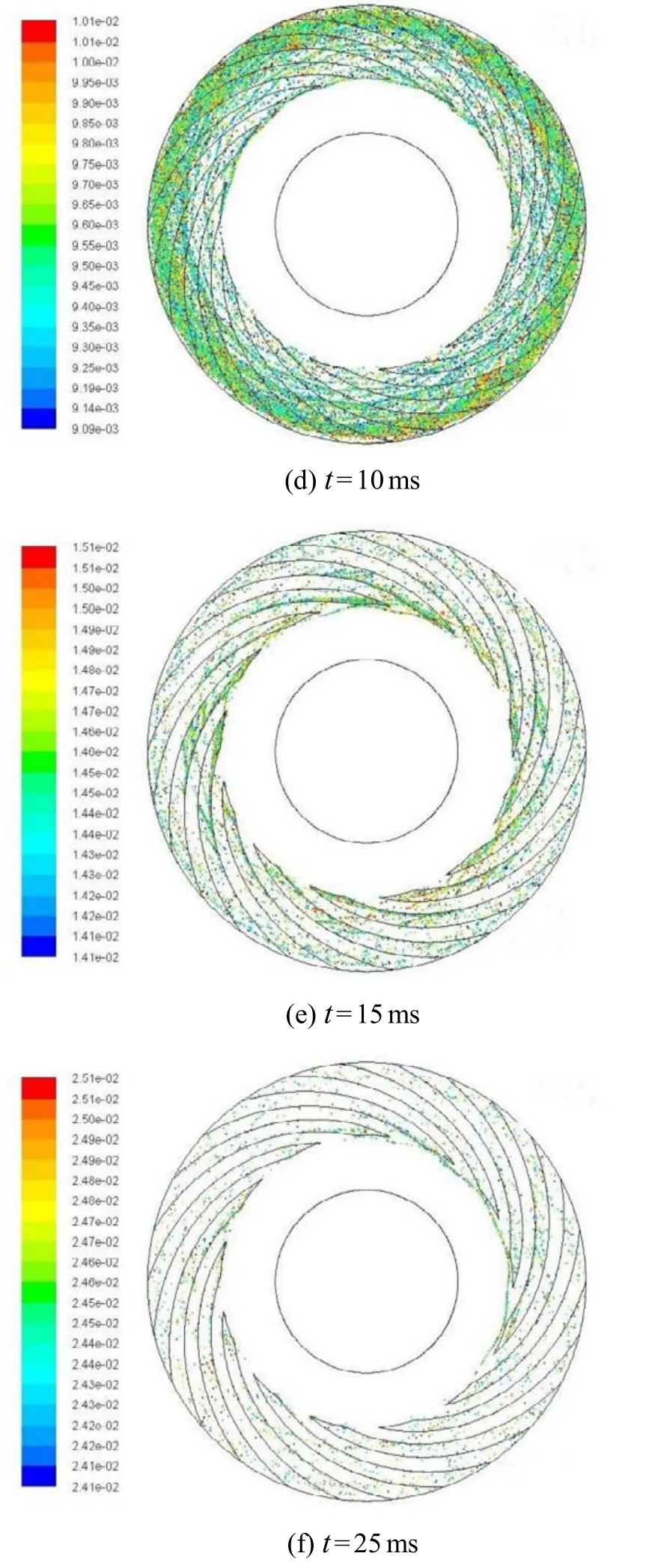
图8 颗粒物分布随时间的变化（γ=4）Fig.8 Distribution of particles with time (γ=4)

以上仿真结果显示颗粒物在轴承中的运动形式与槽深有直接相关。图10(a)和 10(b)进一步给出了槽深比γ=4和γ=1时轴承气膜的气体流线。当γ=4时，气流沿螺旋槽向中心方向泵入，由于螺旋槽壁面的阻挡，在撞击槽壁后反复折回，沿着螺旋槽由外至内折回现象愈加明显；气流运动到槽端后由于坝区的封闭作用进入台区，在离心力作用下以螺旋方式被甩出轴承；由于轴承内圈的封闭，坝区的气流以圆周运动为主。当槽深比减小至γ=1时螺旋槽内流线很少，也没有了槽深模型中的明显折回现象，说明螺旋槽的泵入作用减弱，所以颗粒物几乎不能运动到槽端部。另外由速度场的颜色可知，γ=4轴承间隙的气体流速约为γ=1时的两倍，所以浅槽轴承中颗粒物不易被甩出。气流的运动规律解释了颗粒物的运动与沉积行为，因此可用气膜速度场大致预测轴承内多余颗粒物的运动路径及沉积位置，从而在一定程度上规避费时耗力的颗粒物运动仿真计算。

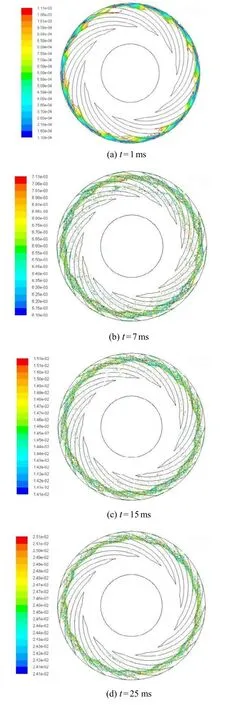
图9 颗粒物分布随时间的变化（γ=1）Fig.9 Distribution of particles with time (γ=1)

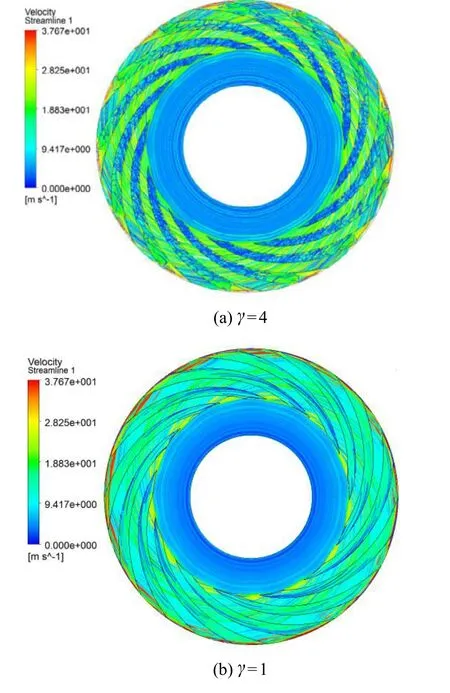
图10 气膜流线图Fig.10 The streamline of bearing

2.3 多余物沉积的典型实验结果

由于多余颗粒物的体积极小，难以观察其在轴承中的运动过程，所以颗粒物在轴承间隙中的运动与沉降规律的实验研究是极其困难的，目前还无法进行。工程实践中，只有在气体动压陀螺仪失效后将其分解，用高倍显微镜才可以观察到轴承表面的颗粒物沉积情况。由于颗粒物直径与轴承外形尺寸相差近万倍，在显微镜实际观察时可通过移动零部件得知颗粒物的分布，却很难得到理想的展示图片。图11给出了联合轴承的止推轴承（γ=4）处的颗粒沉积分布，图中的轴承由于颗粒物的堆积造成表面严重磨损。通过观察可知，颗粒物只沉积在止推轴承中，槽台区居多，坝区也有分布，而径向轴承中几乎没有颗粒物，此分布与仿真结果相近，进一步证明了本文计算的可靠性。

首先，知识产权评议是我国政府制定外商投资准入政策、审查跨国并购的重要依据。对于外国直接投资的准入与限制，关键在于平衡两种不同的价值取向：既要利用外商直接投资的“溢出效应”，通过外资企业关键技术和研发能力的扩散，促进产业结构升级和技术创新；又要防止外资企业垄断和控制核心技术，遏制我国企业技术创新，甚至威胁我国产业安全和产业发展。而要实现这一政策平衡，就必须合理运用知识产权评议，及时分析和掌握相关产业的技术创新状况和知识产权布局状况，准确判断相关技术和知识产权与国家经济安全、国防安全、社会安全等的关系，并据此对外商投资的行业准入政策进行动态调整。

图11 颗粒物沉积分布Fig.11 Deposition of particles

2.4 颗粒物性对颗粒沉积的影响

2.4.1 颗粒直径的影响

不同直径的颗粒物在轴承中存留数量随时间的变化如图12所示，由图可知，不同直径的颗粒物进入轴承的颗粒总数量和变化趋势一致。因为25 ms时留存在轴承中的颗粒数量已稳定，可以用此时的沉积数量作为评判依据。图13为颗粒直径对稳定后沉积数量的影响。由图可知，随着颗粒直径的增大，沉积数量明显减小，这是由于颗粒直径大导致质量大，惯性大，所以离心力大，容易被甩出止推轴承，因此直径小的颗粒物更容易留存在止推轴承中。

图12 不同直径的颗粒物数量随时间的变化Fig.12 Quantity of particles of different diameters vs.time

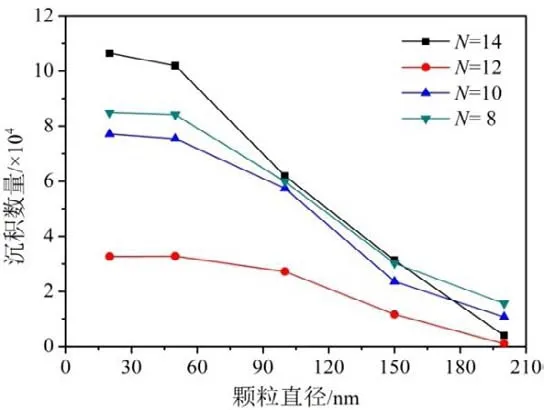
图13 颗粒直径对沉积数量的影响Fig.13 Deposition quantity vs.particle diameter

2.4.2 颗粒密度的影响

图14和图15分别为不同密度的颗粒物在轴承中存留数量随时间的变化和颗粒密度对沉积数量的影响，其中，低分子有机物的密度约为 1g·cm-3，钢的密度约为8g·cm-3。可以看出，随着颗粒密度的增大，沉积数量略有降低，但与颗粒直径的影响相比密度对沉积数量影响较小。

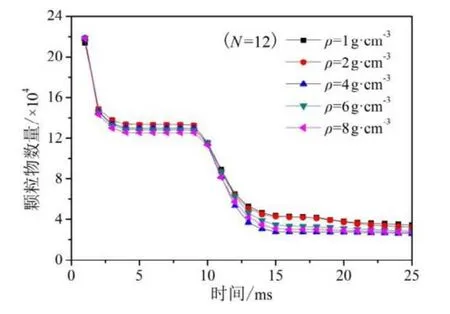
图14 不同密度的颗粒物数量随时间的变化Fig.14 Quantity of particles of different densities vs.time

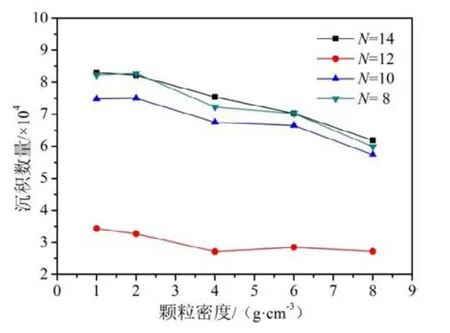
图15 颗粒密度对沉积数量的影响Fig.15 Deposition quantity vs.particle density

2.5 轴承几何参数对颗粒沉积的影响

陀螺电机制造工艺复杂，造价高，以实验形式对轴承结构进行优化、改进是不现实的。本节根据实际需要，以仿真计算的形式对止推轴承的槽数、槽深、螺旋角和槽长等主要结构参数进行了优化，以期弱化颗粒物污染问题。

2.5.1 槽数的影响

颗粒物在不同槽数的轴承中存留数量随时间的变化如图16所示，槽数对进入轴承的颗粒物总数量和数量变化趋势影响较小。

图16 颗粒物数量随时间的变化Fig.16 Quantity of particles vs.time

图17 槽数对沉积数量的影响Fig.17 Deposition quantity vs.groove number

2.5.2 槽深的影响

不同槽深的轴承中的颗粒留存数量随时间的变化如图18所示，该图与图8和9中的颗粒随时间的分布相对应。由图可知，随着槽深的增加颗粒物在槽中的稳定期现象逐渐明显。γ=4（hg=10μm）的轴承中颗粒物数量在1～2 ms时间内急促下降；2～9 ms颗粒在螺旋槽中运动，数量稳定；10 ms颗粒物开始被甩出轴承，数量明显下降；15 ms后下降速度减慢，25 ms时数量稳定。γ=1（hg=2.5 μm）的轴承中颗粒数量变化完全没有稳定期现象，在2 ms后呈现为平缓下降。另外还可从图中看出，随着槽深的增加进入轴承的颗粒总数量增加，这说明随着槽深的增加，螺旋槽泵入作用增强，吸入的气体流量增大，所以吸入的颗粒物增多。图19给出了槽深对稳定后颗粒沉积数量的影响，可见随着槽深的增加沉积数量呈现非线性下降。这是由于槽深增加，从轴承气膜间隙中吸入和排出的气体都增大，速度梯度的减小导致间隙（运动壁面到槽顶部）部分的平均转速升高，颗粒物的离心力随之增大，所以被甩出轴承的数量增多。

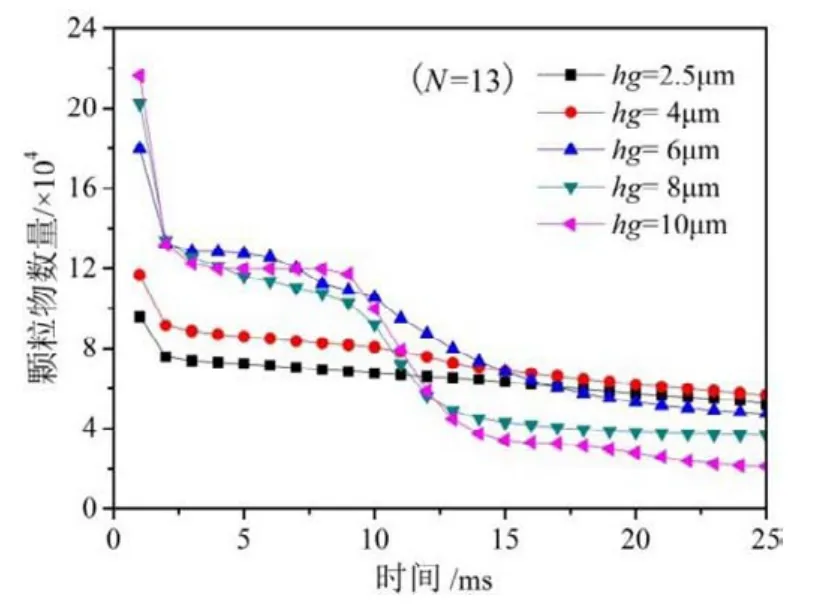
图18 颗粒物数量随时间的变化Fig.18 Quantity of particles vs.time

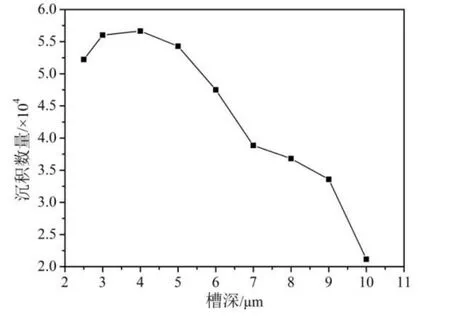
图19 槽深对沉积数量的影响Fig.19 Deposition quantity vs.groove depth

2.5.3 螺旋角的影响

图20 颗粒物数量随时间的变化Fig.20 Quantity of particles vs.time

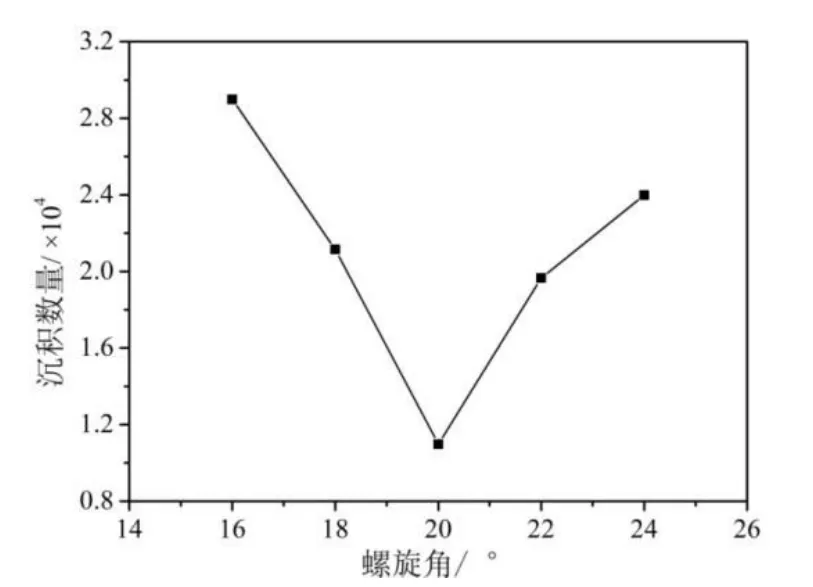
图21 螺旋角对沉积数量的影响Fig.21 Deposition quantity vs.spiral angle

不同螺旋角的轴承中的颗粒留存数量随时间的变化如图20所示。在槽端半径Rg不变的情况下，螺旋角的增加意味着螺旋槽变短，但从图20中可看出，随着螺旋角的增加，颗粒物的槽中稳定期时间却不断增加，此现象也说明了螺旋角越大槽的泵入作用越弱；另外进入轴承的颗粒物数量差别很小，但随着螺旋角的增加，1～2 ms时间内被甩出的颗粒数量先减小后增大，α=20°的轴承中槽中颗粒最多。但颗粒沉积数量（如图21所示）随螺旋角先减小后增大，α=20°的轴承中最少。这是轴承径向的泵入效应与周向的阶梯效应的综合作用，此轴承的气体流量最大。

2.5.4 槽长的影响

不同槽长的轴承中的颗粒留存数量随时间的变化如图22所示。由图可知，随着槽长的增加，颗粒物的槽中稳定期时间增加，但槽中稳定的颗粒数量先增加后减小。进入轴承的颗粒物数量基本相同，沉积数量（如图23所示）随槽长的增加而增大。

图22 颗粒物数量随时间的变化Fig.22 Quantity of particles vs.time

图23 槽长对沉积数量的影响Fig.23 Deposition quantity vs.groove length

3 结 论

通过对螺旋槽气体动压止推轴承进行气固两相流仿真计算，得到了颗粒物在气膜中运动与沉积的典型规律，分析了颗粒物物性和轴承几何参数对颗粒物运动与沉积的影响。主要结论如下：

1）螺旋槽数为12或13，螺旋角为α=20°时，颗粒物在轴承中的沉积最少；适当增加槽深和减小螺旋槽长度也有利于减小颗粒物沉积。

2）多余颗粒物在轴承中的运动与气流的运动密切相关，通过分析气膜的速度场，可大致预测颗粒物的运动与沉积情况。

3）颗粒直径对颗粒在轴承中的运动与沉积规律有较大影响，且直径越小，被吸入的颗粒物越难以排出轴承，但颗粒物密度对颗粒在轴承中的运动与沉积影响较小。