地球重力场模型计算点向径取值对模型重力场元影响

邢志斌，李姗姗，范 雕，张 驰

（信息工程大学 地理空间信息学院，郑州 450001）

地球重力场信息在远程武器的精确打击，航天器的精密定轨、惯性导航系统的精确导航、地球物理现象的研究、资源勘探以及地球环境问题研究等方面起着重要作用[1-5]。地球重力场模型可为以上科学研究、工程实践等提供必要的数据支持。鉴于地球重力场模型的重要意义，世界主要国家无不投入巨大精力研究如何快速精确获取地球重力场信息用于构建地球重力场模型。时至今日，重力场模型已由最初的低分辨率、低阶次发展为目前的高分辨率、超高阶次，重力场信息的获取手段也由原来的陆地重力测量发展为陆地、海上、空中和太空[6]，数据的类型也由最初的单一数据发展为多源数据的融合。在利用超高阶次地球重力场模型计算重力场元时，模型重力场元计算精度受计算点高程的影响，在精度要求较低时，为提高计算效率，通常不考虑高程信息影响，即在球近似下计算，此时，位系数模型中的R r=1[7]。然而，更多的时候对精度要求较高，此时必须考虑高程项的影响，许多文献在计算模型重力场元时为提高计算效率通常会将分母中的计算点向径近似为r=R+H[8-10（]事实上美国国家地理空间情报局（NGA）提供的程序中采用的是计算点真实向径[12]），顾及计算精度与效率，可将计算点高程在球面做泰勒级数展开至一次项[8-9]、二次项或更高次项[10]。由于比例因子R取值地球长半轴[13（]也有文献采用地球平均半径[14]），单纯的将计算点向径近似为r=R+H，将会带来千米级距离误差，同时由于计算区域格网点坐标一般是以大地坐标 (B,L,H)表示，而位系数模型是以球坐标 (r,φ,λ)表示[13]，计算时需要将大地坐标转化为球坐标，在转换时同一纬圈B不同的高度H对应不同的φ，快速计算的前提是同一纬圈对应的φ相等，这些近似误差将不可避免的引入到地球重力场元的计算中。本文针对计算点向径取值展开研究，利用 EGM2008地球重力场模型以模型垂线偏差计算为例分析了r的不同取值造成的距离误差及对地心纬度φ的影响，并与实测垂线偏差进行比对，为顾及计算精度与效率，提出用等效高程代替实际高程进行泰勒级数展开快速计算模型垂线偏差，并分析了其适用性。

1 模型垂线偏差计算

1.1 模型垂线偏差计算公式

计算子午方向和卯酉方向模型垂线偏差的严密公式为[10-11]：

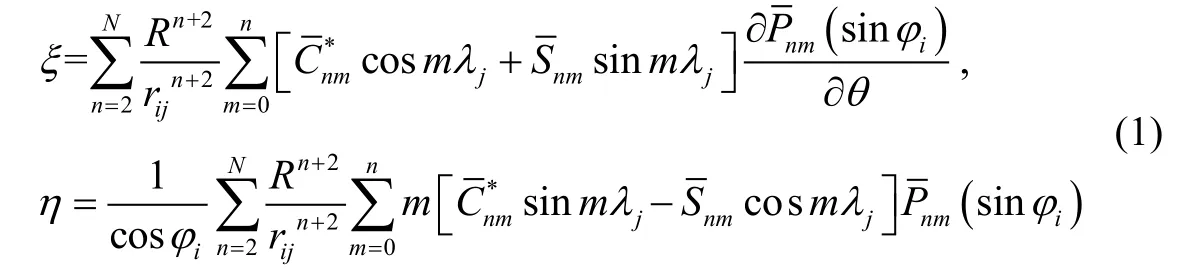
式中，R通常为地球长半轴，表示第 ,( )i j个计算点的地心球坐标，为完全正常化的球谐系数，为完全正常化的缔合勒让德函数，n表示阶，m表示次。

通常我们会使rij=R+Hij，Hij表示计算点的高程，在仅考虑计算效率的情况下，忽略高程项的影响，可直接采用球近似下垂线偏差的计算公式[7]：

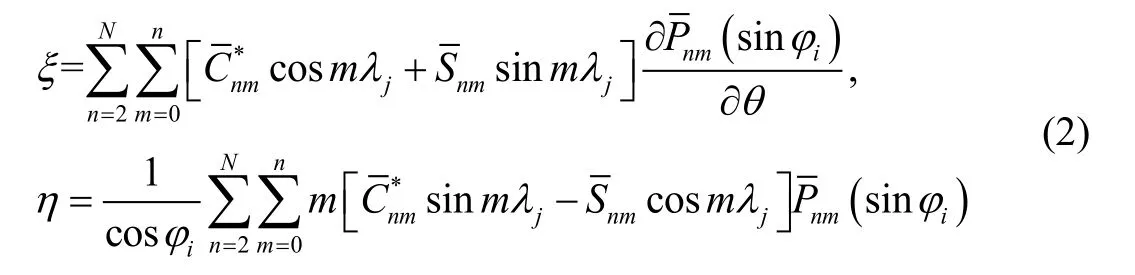
显然式(2)忽略地形影响会降低计算精度，为此一般将式(2)在球面对计算点高程做泰勒级数展开至一阶项得[10,15]垂线偏差子午分量：

和卯酉分量：

为进一步提高精度，可将式(2)按泰勒级数展开至二阶项、三阶项、四阶项，具体展开式及计算过程见文献[10]。

1.2 大地坐标与地心球坐标转换

计算重力场元时，通常给出大地坐标(B,L,H)，而式(1)是在地心球坐标系(r,φ,λ)下表达，因此需要将 (B,L,H)转换到(r,φ,λ)下，再利用式(1)计算模型垂线偏差。首先由式(5)将大地坐标系 (B,L,H)转换到地心空间直角坐标系 (X,Y,Z)下：

三个坐标系之间的关系如图1所示。

图1 ( B , L, H)、( X , Y, Z)和 ( r ,φ, λ)之间关系Fig.1 Relationship among(B , L, H),(X , Y, Z)and (r ,φ, λ)

1.3 模型垂线偏差计算公式分析

1.3.1 向径误差分析

采用式(1)计算模型垂线偏差时，由式(6)确定每个计算点的向径，将会耗费大量的时间，通常会令ri=R+Hi，由于R的值为地球长半轴，因此除赤道区域以外，在其他区域采用这种近似将会带来很大的距离误差。如果令ri=R+Hi，R=6371000.0m，表示地球平均半径，这样会在中纬度地区改善距离精度，但在赤道和两极地区则又会失真。此时，为提高计算效率和距离精度，可计算出同一纬圈椭球面向径r0再加高程Hi，即r=r0+Hi。

为比较以上三种近似带来的误差影响，分别令：

采用5′×5′全球陆地和海底地形格网数据（由ETOPO1数据平滑后得到，如图2所示）计算每个点的向径，并与由式(6)计算的向径值进行比较，统计结果如表1、图2～5所示。

表1 不同近似值与真值之差统计量（单位：m）Tab.1 Differences between different approximations and true values (unit: m)

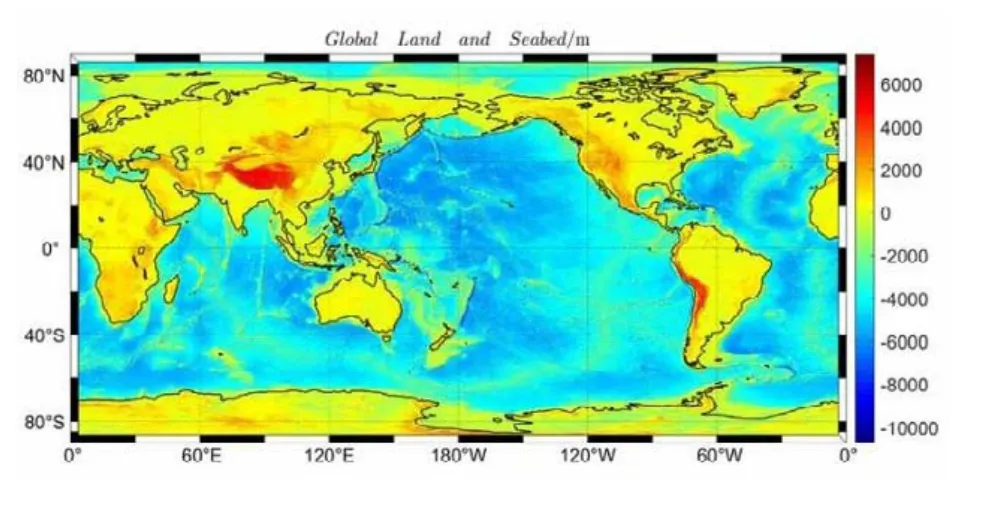
图2 全球陆地与海底地形Fig.2 Global land and seabed topography

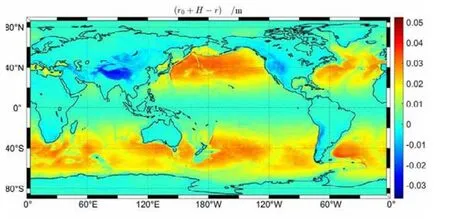
图3 参考椭球面向径和地面高程之和与真值之差 ( vr0 +H- r)Fig.3 Differences between the summation of reference ellipsoid and elevation and true values (vr0 +H- r)

图4 地球长半轴和地面高程之和与真值之差(vR+H-r)Fig.4 Differences between the summation of semi-major axis and elevation and true values (vR+H-r)

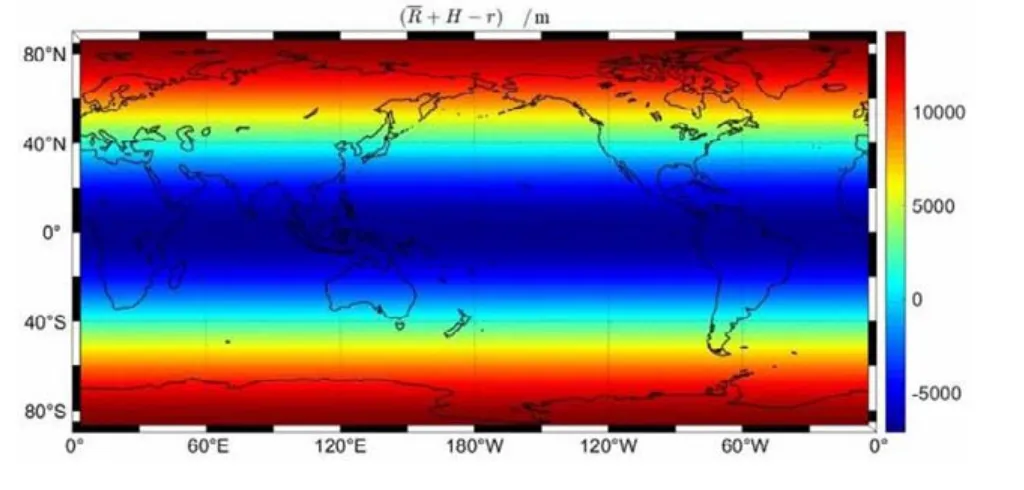
图5 地球平均半径和地面高程与真值之差(v )Fig.5 Differences between the summation of Earth' mean radius and elevation and true values (v )

由以表1和图2～5可以看出，采用不同的近似值，距离误差相差很大。在三个近似值中，近似值（1）的精度最高，与真值相比只有厘米级的误差，近似值（2）、（3）与真值相比，误差达到了km级，并且这些误差具有系统性，即同一纬圈附近的误差基本一致，近似值（1）在赤道地区误差最小，向两极逐渐增大，而近似值（3）造成的误差在南北纬30°附近最小，两极地区最大。

1.3.2 不同向径对球心纬度影响分析

由式(5)(6)可知，地心纬度φ与高程H有关，因此，同一纬圈B如果格网点的高程不同，则φ不同。但是在模型重力场元计算中，我们通常认为同一纬圈对应的φ相同，为分析这种近似误差，分别计算格网点真实高度（海深）处的地心纬度φ以及对应的参考椭球面上的地心纬度φ0，统计结果如表2、图6所示。

表2 椭球面地心纬度与计算点地心纬度之差统计量（单位：″）Tab.2 Differences between ellipsoid and calculation points' geocentric latitude (unit: arc second)

图6 参考椭球面地心纬度与实际点地心纬度之差 ( vφ0-φ)Fig.6 Differences between references ellipsoid surfaces'geocentric latitude and real geocentric latitude (vφ0-φ)

由表2、图6可知，由地球上实际高程（海深）造成的地心纬度误差很小，绝对值最大值也就 1″左右，这对于最高分辨率5′×5′的地球重力场模型来说是可以忽略不计的。由图6可以看出，地心纬度误差具有一定的系统性，在北半球海洋区域多为正值，而南半球海洋区域多为负值，并且相比于参考椭球面地心纬度φ0，高程为正会使得地心纬度有增大的趋势。

1.4 模型垂线偏差快速计算

向径不同取值之间存在 km级的差距，采用式(3)(4)快速计算模型垂线偏差将会产生误差，但是逐点计算又会耗费大量时间。此时可采用等效高程Hi′j代替式(3)(4)中Hij，即垂线偏差子午分量：和卯酉分量：

为提高计算效率，r0或r可提前计算出，可采用向量运算的方式一次性计算出计算区域的等效高程，向量运算的计算方法可参考文献[10][17]。

为分析模型垂线偏差快速计算方法的适用性，选择我国青藏高原一 6°×6°地势变化剧烈区域，采用式(7)(8)，由EGM2008地球重力场模型计算分辨率5′×5′的子午方向和卯酉方向格网垂线偏差，与(1)式计算的模型垂线偏差作对比。计算区域高程如表3、图7所示。

表3 研究区域高程统计（单位：m）Tab.3 Statistics of study area elevations (unit: m)

图7 计算区域高程Fig.7 Elevations of study areas

根据表3、图7可知，该区域地势变化相当复杂，平均高度接近4000 m，但最低高度只有27 m，而最高高度接近7000 m。将前50行格网分成一部分，后70行格网分成一部分，两部分高程变化差距很大，前50行格网的高程标准差只有百米量级，而后70行格网则高达近2 km。展开至不同阶次泰勒级数计算模型垂线偏差与严密公式计算结果残差如图8～11所示（左图为子午方向、右图为卯酉方向），整体统计如表4所示，分区统计如表5所示。

由表4可知，就整个区域而言，展开阶次对精度没有实质性的影响，并且子午方向的精度一直低于卯酉方向的精度。对模型垂线偏差计算精度进行分区统计时（如表5所示），前50行的精度远远优于后70行的精度，并且展开至二阶项以后其精度趋于稳定。

后 70行计算结果与文献[10]给出的结果有一定的出入，分析原因主要有：

1）文献[10]中的计算点向径取值r=R+H要大于计算点实际向径km级，这相当于计算的是高空的重力场元在一定程度上平滑了重力场信号，重力场元与高程可近似为线性关系，因此泰勒级数展开至不同阶次，对计算精度提升较大；

表4 展开至不同阶次垂线偏差整体精度统计（单位：″）Tab.4 Accuracy statistic of extended to different orders for all study areas (unit: arcsec)

表5 展开至不同阶次垂线偏差分区精度统计（单位：″）Tab.5 Accuracy statistic of extended to different orders for different areas (unit: arcsec)

图8 垂线偏差展开至一阶项与模型真值之差Fig.8 Differences between true values and extended to first-order terms

图9 垂线偏差展开至二阶项与模型真值之差Fig.9 Differences between true values and extended to second-order terms

图10 垂线偏差展开至三阶项与模型真值之差Fig.10 Differences between true values and extended to third-order terms

图11 垂线偏差展开至四阶项与模型真值之差Fig.11 Differences between true values and extended to forth-order terms

2）文献[10]中计算区域的地势复杂程度远低于图7区域，重力场变化的剧烈程度也低于图7区域；

3）式(7)(8)泰勒级数展开至一阶项，本质上是利用径向梯度延拓距离H′，一方面重力场模型中很难含有地表的梯度信息，另一方面H′过大会造成延拓发散。

由此可知，利用式(7)(8)快速计算模型垂线偏差并不完全适用于任意地区，在地势变化复杂的区域需要综合考虑各方面的因素。

2 实验对比分析

2.1 近似值与模型垂线偏差真值比较

为分析计算点向径误差对模型垂线偏差的影响，选择图7所示区域，分别将向径设为：1）r=r0+Hi；2）

计算分辨率 5′×5′的子午方向和卯酉方向格网垂线偏差，与采用真实向径计算的模型垂线偏差作对比。统计结果如表6、图12～19所示。

根据图12、图13可知，该地区垂线偏差变化比较剧烈，最大值可达1′多。由表6可知，当r=r0+Hi时计算的模型垂线偏差与真值之差非常小，RMS不会超过0.01″（图14、图15所示），远低于当前一等天文垂线偏差的测量误差（0.3″），这说明在计算模型垂线偏差时这种近似是可行的。

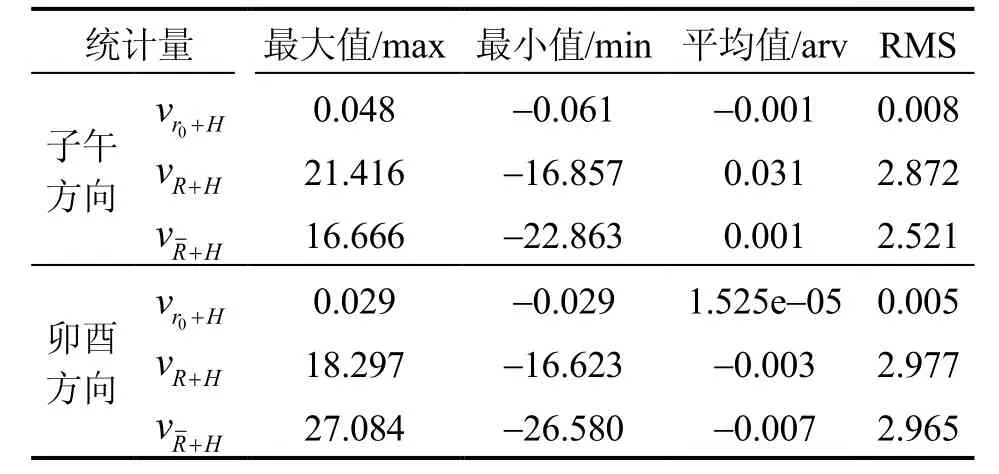
表6 垂线偏差不同近似值与模型真值之差统计（单位：″）Tab.6 Differences between different approximations and model true values (unit: arcsec)

图12 子午方向模型垂线偏差真值Fig.12 Model vertical deflection true values in meridian direction

图13 卯酉方向模型垂线偏差真值Fig.13 Model vertical deflection true values in prime direction

图14 子午方向模型垂线偏差残差1Fig.14 Residual 1 of model vertical deflection in meridian direction

图15 卯酉方向模型垂线偏差残差1Fig.15 Residual 1 of model vertical deflection in prime direction

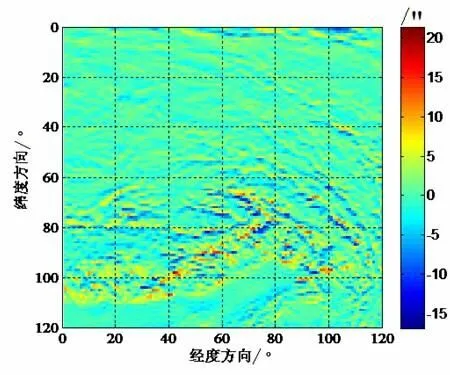
图16 子午方向模型垂线偏差残差2Fig.16 Residual 2 of model vertical deflection in meridian direction

图17 卯酉方向模型垂线偏差残差2Fig.17 Residual 2 of model vertical deflection in prime direction

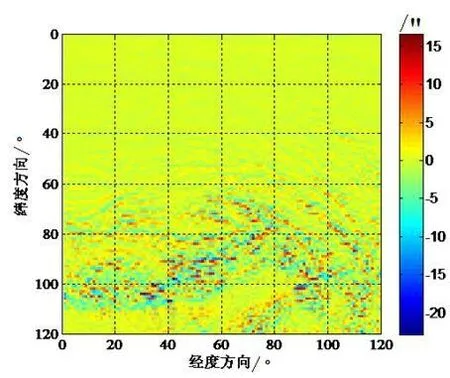
图18 子午方向模型垂线偏差残差3Fig.18 Residual 3 of model vertical deflection in meridian direction

图19 卯酉方向模型垂线偏差残差3Fig.19 Residual 3 of model vertical deflection in prime direction

2.2 模型值与实测值比

为比较计算点向径r的不同取值对模型垂线偏差计算结果的影响，分别计算了25个实测天文大地垂线偏差点在四种取值情况下的模型垂线偏差，与其真值比较，残差统计结果如表7、图20、图21所示。

由表7、图20、图21可知，在子午方向上，采用计算点向径真值与近似值 1（r=r0+Hi）计算的模型垂线偏差与实测数据相比，精度是一致的，相比于其他两种近似（ri=R+Hi和垂线偏差计算精度有了很大的提高，并且这样的精度与EGM2008模型在美国本土的精度是基本一致的。但是在卯酉方向，采用向径真值和近似值 1计算垂线偏差精度却有了略微的降低，分析原因可能是受我国西高东低地势的影响，由于仅采用了25个实测点进行验证，因此造成这种现象的原因还需做进一步研究。

图20 子午方向垂线偏差残差（单位：″）Fig.20 Residual of vertical deflection in meridian direction (unit：arc second)

表7 垂线偏差模型值与实测值之差统计（单位：″）Tab.7 Differences between model values and measured values (unit: arc second)

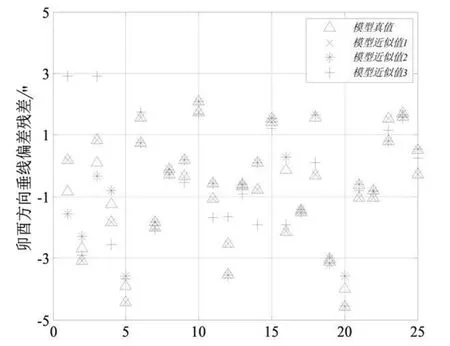
图21 卯酉方向垂线偏差残差（单位：″）Fig.21 Residual of vertical deflection in prime direction (unit：arcsec)

3 结 论

本文以模型垂线偏差计算为例，分析了计算点向径不同取值造成的距离误差及对地心纬度的影响，进而通过实验分析了距离误差对模型垂线偏差计算精度的影响。实验表明：1）r=r0+Hi距离误差造成的影响可忽略不计；2）r=R+Hi在赤道地区的影响很小，向两极逐渐增大；3）r=+Hi在南北纬30°地区影响最小；4）实际计算点的地心纬度与计算点对应的参考椭球面上点的地心纬度之差最大值在 1″左右，对垂线偏差造成的影响绝对值最大不超过0.07″，这些影响对模型重力场元计算可忽略不计，在格网模型重力场元计算时同一纬圈可只计算一次缔合勒让德函数，为快速计算带来了极大的方便。与25个实测点垂线偏差进行比较，r取真值与r=r0+Hi计算的子午方向垂线偏差结果一致，且精度最高，达到了EGM2008重力场模型在美国本土的精度，但是卯酉方向垂线偏差计算的精度却略低于r=R+Hi计算的精度，由于用来比较的实测数据太少，因此还很难分析出精度变差的原因。用计算点等效高程Hi′j代替实际高程Hij，可在原有程序的基础上利用式(7)(8)快速计算格网模型垂线偏差，但是其适用范围是有限的，并不适用于地势变化剧烈地区，如若进一步提高计算精度可采用在椭球面展开的方法[15]。