双轴旋转惯导系统转轴倾角在线标定方法

陈 刚，刘建春，孙伟强，王俊柱，赵凤昊

（天津航海仪器研究所，天津 300131）

双轴旋转惯导系统通过双轴旋转有效地调制了惯性元件的误差[1-3]，相比捷联惯性导航系统，大幅提高了长时间自主导航能力。双轴旋转惯导系统的机械编排与捷联惯导系统的不同之处在于双轴旋转惯导系统的惯性解算得到的姿态进行解耦后才可以得到载体姿态[4]。转轴倾角将会在双轴旋转惯导系统姿态解耦过程中，引入一个随系统双轴旋转波动的姿态误差。此姿态误差在未补偿转轴倾角时，波动幅值在几角分到十几角分，因此标定补偿系统转轴倾角对保证姿态精度十分必要。刘冲研究了双轴旋转惯导系统转轴倾角标定方法，其要求将系统置于实验室内的静基座上，然后通过观察系统静态下的姿态输出随双轴旋转的波动，标定出转轴倾角的大小[5]。但是如果双轴旋转惯导系统在码头系泊时更换惯组，使用此方法难以标定出转轴倾角。鉴于此，本文提出一种系泊状态下转轴倾角标定办法。

1 转轴倾角的误差传播特性

1.1 转轴倾角的定义

首先定义本文数学推导过程中所涉及的坐标系。定义导航坐标系n 系为地理坐标系。由于旋转机构两个旋转轴经过结构工装标定后近似正交，定义旋转机构坐标系r 为以旋转机构内轴指向为y轴，外轴指向为z轴，构成的右手正交坐标系，并由定义可知r系会随旋转机构一起转动。

记待补偿系统计算导航坐标系为 n1系，惯组坐标系为p 系，载体坐标系为b 系，未补偿转轴倾角时由p系对两个轴的转角进行姿态解耦后得到的坐标系为b1系。记参考系统计算导航坐标系为 n1′系。设当两个轴的转角均为零时，b系与r系重合。

定义双轴旋转惯导系统的转轴倾角为r系相对于p系的欧拉角。本文设双轴旋转惯导系统的转轴倾角，图1为转轴倾角示意图，图中Ox′、rOyr′ 分别为坐标轴Oxr、Oyr在面Oxp yp的投影，Ozr′为坐标轴Ozr在面Oyp zp的投影。

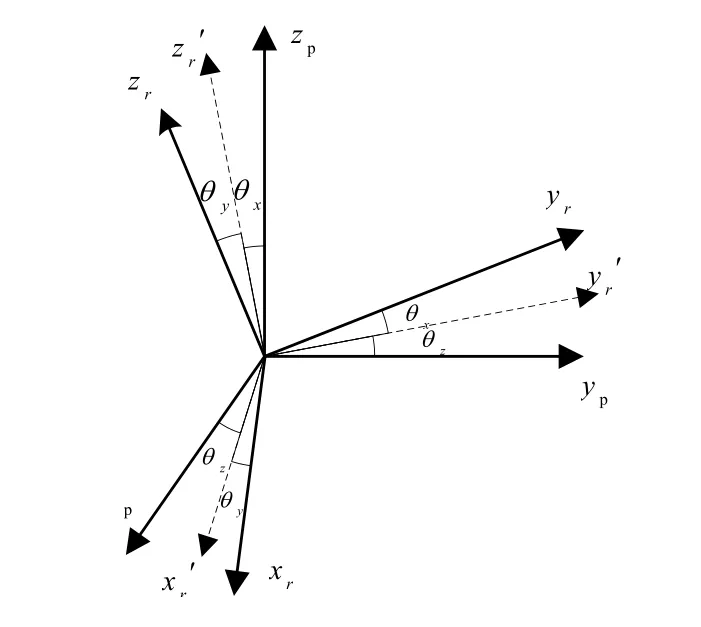
图1 转轴倾角示意图Fig.1 Schematic of the fixing error angles between axes and IMU

1.2 转轴倾角引起姿态角波动的数学模型

待补偿双轴旋转惯导系统的姿态误差可分为两部分，由转轴倾角引起的姿态波动φ和由惯性元件误差引起的姿态误差角φn，其中，φ为 b1系相对于b系的姿态波动，对应的姿态误差矩阵为系相对于n 系的姿态误差，对应的姿态误差矩阵为参考系统的姿态误差为由惯性元件误差引起的 n1′系相对于n 系的姿态误差角φn′，其对应的姿态误差矩阵为

双轴旋转惯导系统姿态矩阵的解算过程可分两步。首先通过惯性元件的输出，更新p 系相对于 n1系的姿态矩阵然后在的基础上根据旋转机构测角元件读角及装订的转轴倾角解算得到。若不补偿转轴倾角，则在第二步解算中将转轴倾角设为这将会在解算结果中引入姿态波动φ，从而解算得到姿态矩阵

设双轴旋转过程中系统内框、外框分别相对初始位置依次绕其转轴逆时针转角为内、外转轴上的测角元件输出分别为α1、β1，测角噪声分别为有：

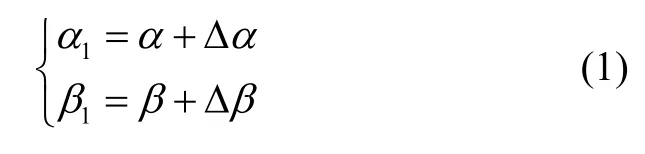
并且设

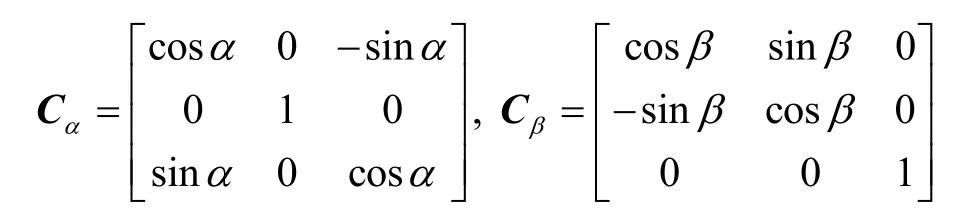
使p 系依次绕其z轴和x轴转动θz、θx角度得到p1系，其y轴与r系的y轴重合，从而为补偿旋转机构绕y轴的转角α创造条件。在 p1系与r系y轴重合的基础上，继续绕其y轴转动θy角度，得到 p2系，与r系完全重合，从而为补偿旋转机构绕z轴的转角β创造条件。记根据以上分析，补偿转轴倾角时，姿态矩阵Cbn1的

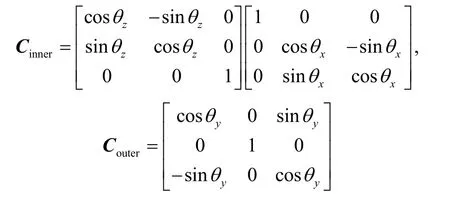
计算过程可以表示为：

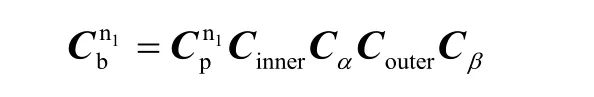
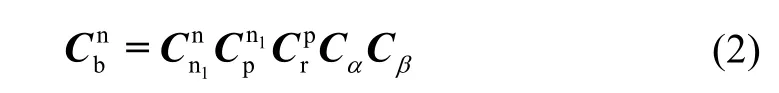
当

由式(2)(3)得φ对应的姿态误差矩阵为：

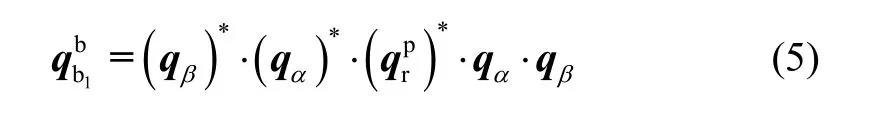
由于θ各元素均为小量，从而θ可以看作从p系

式(4)转换为四元数连乘的形式为[6]：转动到r 系的等效旋转矢量[7]。

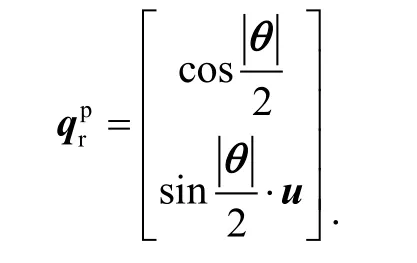
其中，

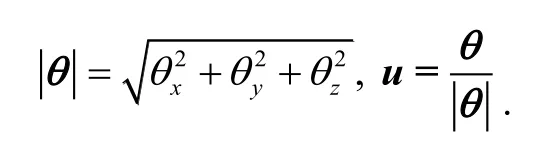
将式(6)代入式(5)中可以推导出：

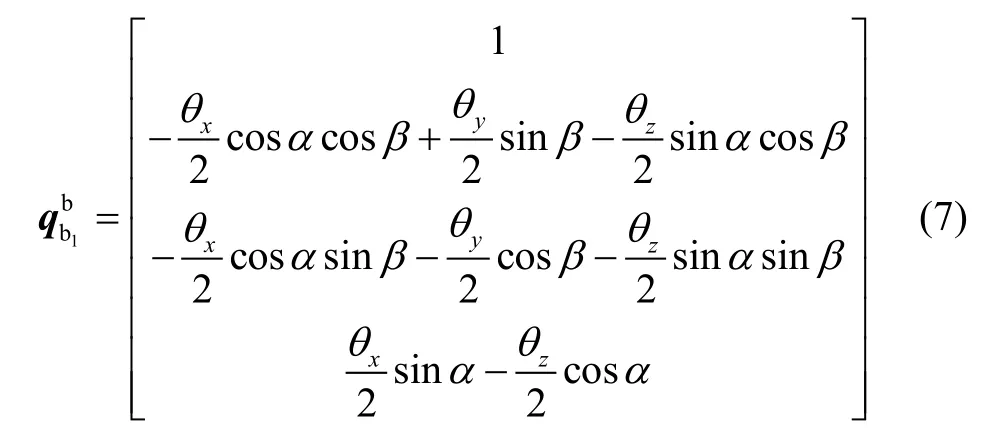
式(7)与式(8)对应元素相等，可以得出：

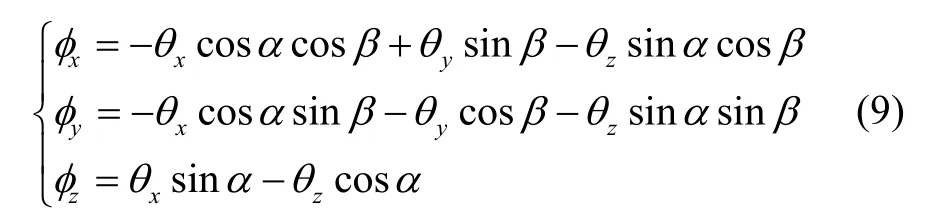
将式(1)代入式(9)可以得到转轴倾角引起的姿态波动的数学模型为：

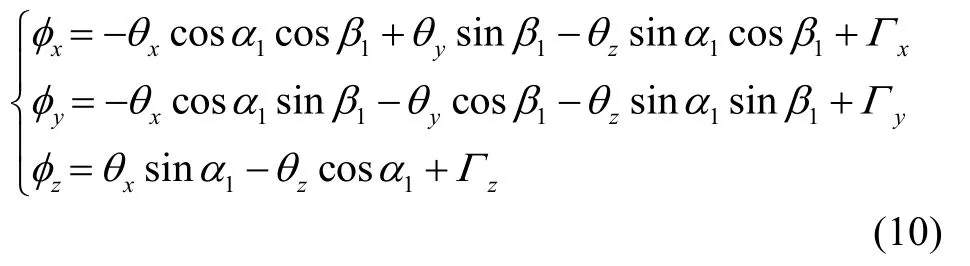
其中，

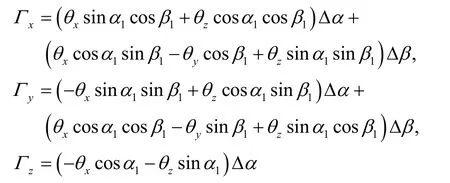
1.3 待补偿系统与参考系统的姿态差数学模型

本文以待补偿系统与参考系统的姿态差作为观测量标定待补偿系统的转轴倾角。设参考系统与待补偿系统同刚性基座安装，已补偿转轴倾角，并且两套系统均已正确补偿姿态零位。设由时间同步误差引起的两套系统之间姿态差为φts，对应的姿态矩阵为Cφts，参考系统的姿态零位为φ0，对应的姿态矩阵为Cφ0。

待补偿系统输出姿态为 b1系相对于 n1系的姿态，其对应的姿态矩阵可以表示为：

参考系统输出姿态为b系相对于系的姿态，其对应的姿态矩阵可以表示为：

设两套系统输出姿态差为φb，其对应的姿态误差矩阵可以表示为

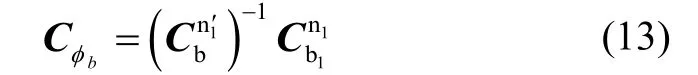
由式(11)～(13)可得：

由于φb、φn、φn′、φts、φ均为小量，从而式(14)可以表示为：

展开并略去二阶小量得到：

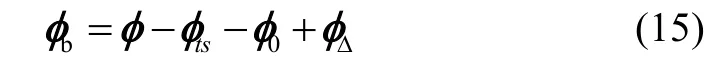
对φb进行微分得待补偿系统与参考系统的姿态差的微分方程为

由式(16)可得，参考系统的姿态零位误差在可以被看作小量的情况下，对转轴倾角标定影响可被忽略。将式(16)展开可得：

2 转轴倾角标定方案

2.1 FIR低通滤波器设计

式(17)中φts、φΔ均与载体摇摆的剧烈程度有关，并且φts受到载体摇摆的影响较大，若两套系统之间的时间同步误差为数毫秒，当海况较差时，φts波动幅值可达到数角分，相比φ为不可忽略的量。

若将系统姿态输出中的载体摇摆分量滤掉，然后计算φb，可以消除φts对转轴倾角标定的影响。有限长单位冲击响应（FIR）滤波器具有线性相位的特点[8]，保证了滤波器对各频率信号的延时是固定的，便于在标定转轴倾角时补偿滤波后姿态角与转轴读角之间的时间差。

首先对转轴倾角引起的姿态波动进行频域分析。图2为转轴倾角θ=[2.4′ 3.3′ 6.4′]T的双轴旋转惯导系统静态时输出姿态波动与某次系泊实验舰船姿态波动的频域图。由图2可以看出，转轴倾角引起姿态波动的频率主要集中在 0.05 Hz以下范围。而船系泊时纵摇与横摇摇摆的频率较高，多在 0.06 Hz以上，艏摇频率较低与转轴倾角引起姿态波动的频段相重合。相同波动幅值下，摇摆频率越高与时间同步误差相耦合引起的姿态误差越大，对转轴倾角标定影响越大。可以采用低通滤波器滤除待补偿系统与参考系统系泊状态下的高频姿态波动，以减小其与时间同步误差耦合对转轴倾角标定的影响。

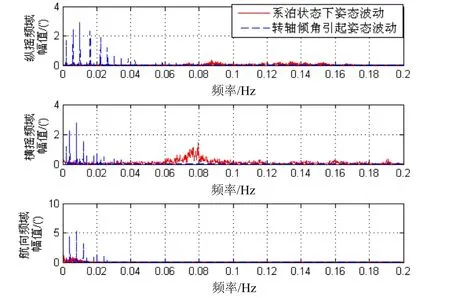
图2 转轴倾角引起的姿态波动频域图Fig.2 Frequency domain of the attitude fluctuation caused by the fixing error angles between axes and IMU

本文使用窗函数法设计FIR滤波器[9]。针对系统1Hz姿态输出所设计的FIR低通滤波器，截止频率为0.06 Hz，阶数为400阶，窗体为布莱克曼窗，其幅频特性曲线如图3所示。

设置待补偿双轴旋转惯导系统转轴倾角为θ=[2.4′ 3.3′ 6.4′]T，两套系统时间同步误差为5 ms，摆幅值与周期如表1所示，得到的滤波前和滤波后待补偿系统相对参考系统姿态波动分别如图4～6中虚线和实线所示。由图4～6可以看出，滤波前计算得到的待补偿系统与参考系统姿态差中包含载体摇摆与时间同步误差的耦合误差，而在滤波后此误差被基本滤除。

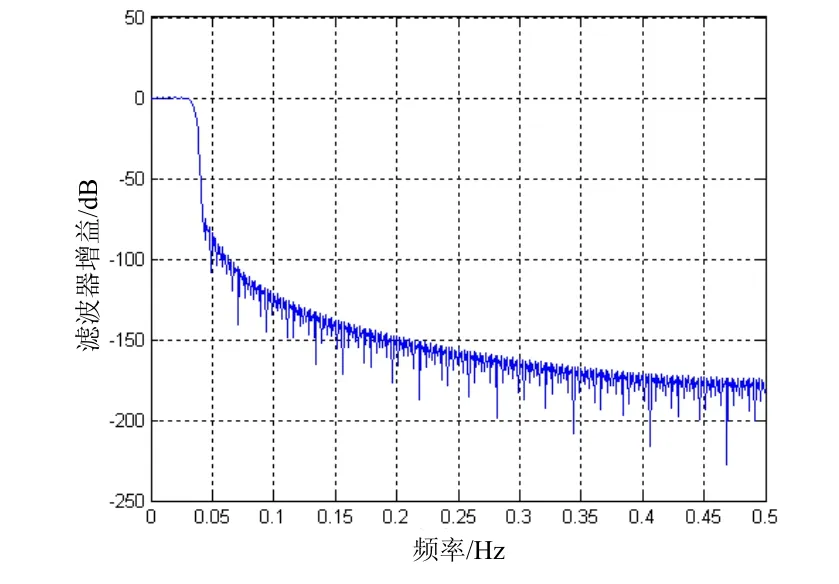
图3 FIR滤波器幅频特性曲线Fig.3 Curves of FIR filter's amplitude-frequency

图4 待补偿系统相对参考系统的纵摇误差波动Fig.4 Pitching error fluctuation of the compensated system relative to the reference system

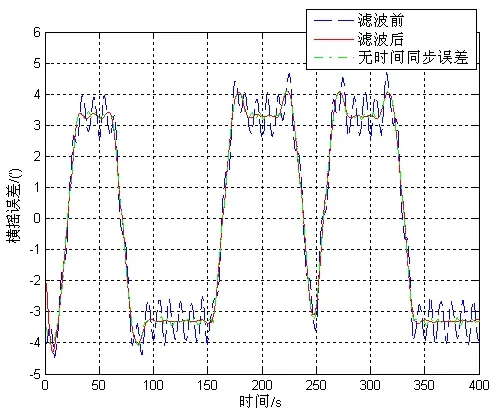
图5 待补偿系统相对参考系统的横摇误差波动Fig.5 Rolling fluctuation of the compensated system relative to the reference system

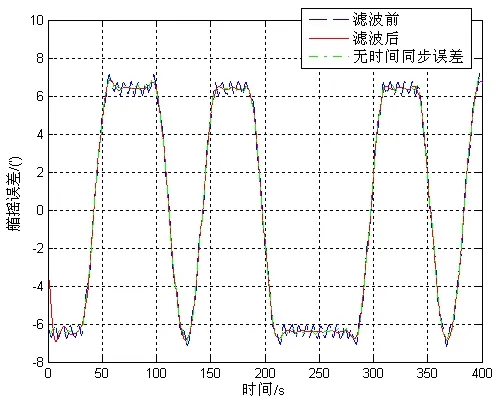
图6 待补偿系统相对参考系统的航向误差波动Fig.6 Heading error fluctuation of the compensated system relative to the reference system

表1 摇摆幅度和周期Tab.1 Amplitude and period of the swing

2.2 状态方程建立

设状态向量为

由式(16)得到系统的状态方程为：

其中，

由于在使用FIR滤波器将载体姿态输出中包含的载体摇摆分量完全滤去的理想情况下，为常量。因此有相比为小量，亦可作噪声处理。

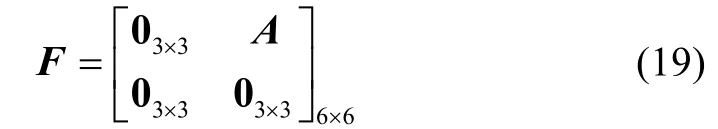
其中，

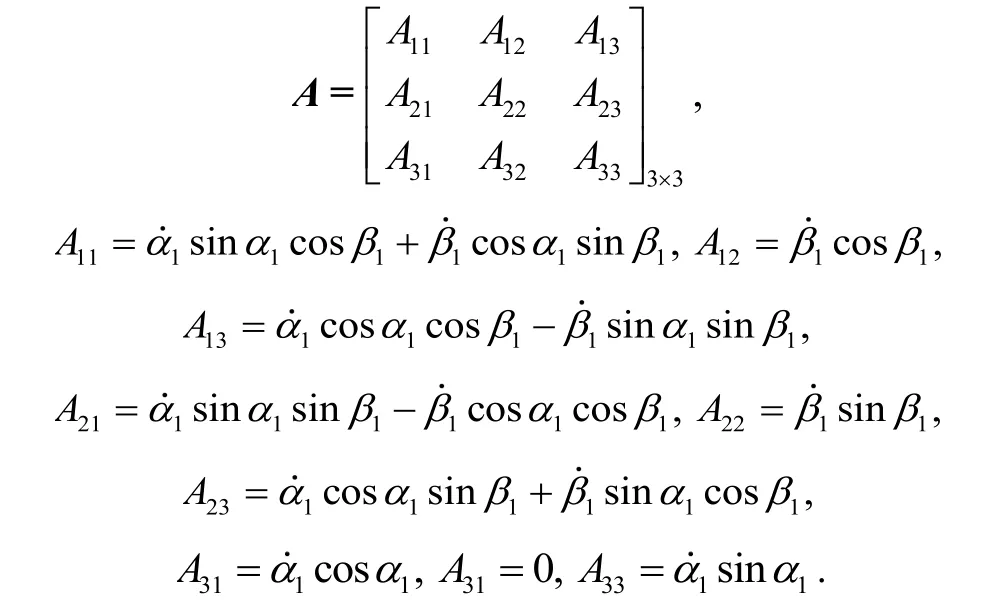
2.3 量测方程建立

设系统量测量Z为参考系统与待补偿系统输出姿态经过同一FIR滤波器滤波后的欧拉角误差，其对应的姿态矩阵通过式(12)计算得到。可得量测方程为：

将式(18)(20)离散化，再采用Kalman滤波方法进行估计，即可获得转轴倾角的最优估计，实现转轴倾角的标定[10]。

2.4 转轴倾角标定流程

由以上推导分析得到的双轴旋转惯导系统系泊状态下转轴倾角标定流程如图7所示。

图7 转轴倾角标定流程示意图Fig.7 Schematic of calibration process for the fixing error angles between axes and IMU during digital

3 仿真验证

3.1 数字仿真验证

数字仿真中设置待补偿双轴旋转惯导系统误差如表2所示，时间同步误差为5 ms，摇摆参数如表1所示。

表2 数字仿真误差项设置Tab.2 Error settings for digital simulation

卡尔曼滤波器初值设置如下：

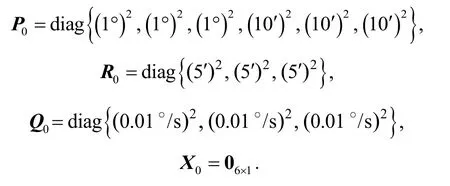
仿真结果如图8所示。卡尔曼滤波器收敛时，所估计转轴倾角为，估计误差为

由图8可以看出，θx、θy在滤波开始后即迅速收敛，θz在滤波开始一段时间后才开始收敛。其原因是转轴倾角的收敛顺序和转位次序有关。在第一个转位次序中，内框转角α1=0 °，内框转动角速度α1=0(°)/s，根据式(19)可得：

从而矩阵F第三列元素为零，第一个转位次序所激发的姿态波动与θz无关，从而θz在滤波开始时没有收敛趋势。

当进行第二个转位次序，内框转动外框停止时，有=0 (°)/s，由式(19)可得：

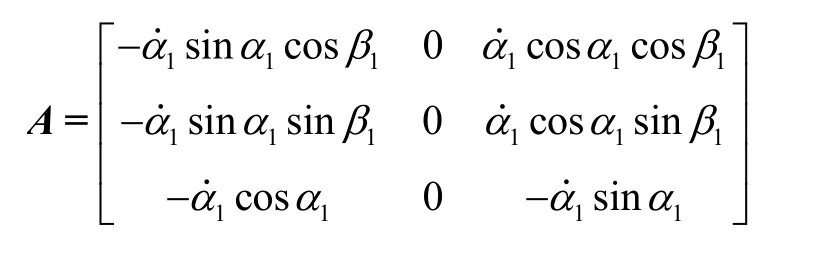
从而第二个转位次序中，矩阵F第三列元素不为零，θz可被观测，迅速收敛。

图8 数字仿真转轴倾角卡尔曼滤波估计值Fig.8 Kalman filter's output of the fixing error angles between axes and IMU during digital simulation

3.2 半实物仿真验证

本文采用安装在摇摆台刚性基座上的两套双轴激光惯导系统进行半实物仿真实验，分别命名这两套系统为1#系统、2#系统，其中1#系统已补偿转轴倾角，作为参考系统，2#系统未补偿转轴倾角，作为待补偿系统。两套系统精对准结束后正确补偿姿态零位。实际在舰船系泊状态下进行转轴倾角标定时，船舶摇摆姿态的频谱比较复杂，经FIR滤波后待补偿系统与参考系统的姿态输出中仍存在未被滤掉的载体摇摆姿态。

为充分考虑实际舰船系泊情况，进行3次试验，设置摇摆台的摇摆幅度和频率如表3所示，分别测试本方法在静止状态、低频摇摆与高频摇摆下的转轴倾角标定效果。

如图9～11所示为3次实验的转轴倾角标定结果，3次实验转轴倾角分别收敛于比较实验1和2的实验结果可以得出载体高频摇摆对转轴倾角标定几乎无影响。

表3 半实物仿真摇摆台设置Tab.3 Swing table setting in semi-physical simulation

图9 2#系统θx标定结果Fig.9 Calibration result of the 2# system's θx

图10 2#系统θy标定结果Fig.10 Calibration result of the 2# system's θy

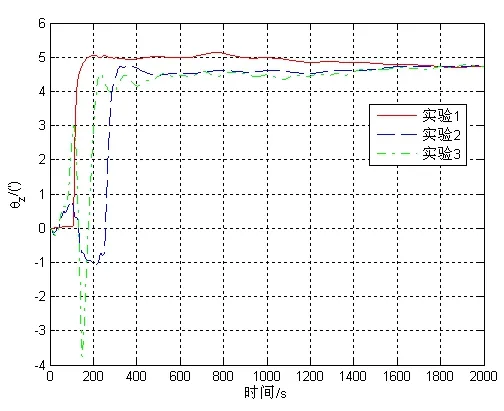
图11 2#系统θz标定结果Fig.11 Calibration result of the 2# system's θz

比较实验1和3的实验结果可以得出低频摇摆对标定精度影响较小，分析其原因是低频摇摆频率较低、幅值较小，与两套系统之间时间同步误差耦合引起的角度误差相比转轴倾角引起的姿态波动为小量，并且波动规律不完全相同，因而对转轴倾角标定的收敛过程中的波动影响较大，而对收敛精度影响较小。

由3次实验的实验结果可以得出，本方法在静态与系泊状态下转轴倾角标定精度相当。

4 结 论

本文建立了转轴倾角引起姿态波动的数学模型，推导了状态方程与量测方程，并设计了FIR低通滤波器消除参考系统与待补偿系统间时间同步误差的影响，进而实现了系泊状态下双轴旋转惯导系统转轴倾角的标定。

本文所提出的方法能够实现转轴倾角的自动标定，对提高系统的可维护性具有重要意义。