基于载噪比加权融合的异步伪卫星室内定位方法
夏 炎,潘树国,蔚保国,高 旺,甘兴利,王欣怡
(1.东南大学 仪器科学与工程学院,南京 210096;2.卫星导航系统与装备技术国家重点实验室,石家庄 050081;3.中国电子科技集团公司第五十四研究所,石家庄 050081)
随着基于位置的服务(Location Based Service,LBS)在生活以及军事上的应用越来越广泛,人们对全球导航卫星系统(Global Navigation Satellite System,GNSS)的应用场景也提出了更多的要求。GNSS在开阔环境中能够提供连续可靠的高精度位置信息,但无法解决遮挡环境下导航的“最后一公里”问题。目前基于无线信号的室内定位技术主要有Wi-Fi[1]、蓝牙[2]和超宽带[3](Ultra-Wide Bandwidth,UWB)等,但Wi-Fi和蓝牙技术通常只能达到米级定位精度,且建立及维护指纹库需要巨大的工作量。UWB技术虽然能达到更高的精度[4],但其信号传输距离短,需要精确的时钟同步,系统建设成本昂贵,难以大面积部署和应用。
伪卫星技术因其信号覆盖范围广、信号体制与GNSS相同,能与GNSS实现室内外无缝定位,正受到越来越多的重视,在重点区域和特定场所乃至军事领域有着非常广阔的应用前景。目前国际上技术最成熟、应用最广的伪卫星系统是Locata,能满足自动控制、露天采矿、港口测量、变形监测等领域的精密定位需求,通过特殊的天线分集技术抑制多径效应,可以在室内进行工业级、厘米级的定位[5-6],但 Locata系统要求伪卫星必须保持严格的时间同步,这对设备的要求极高,会导致巨大的部署成本和实施难度。文献[7]为了规避时间同步问题,采用基于伪卫星信号载噪比的加权质心方法进行了室内定位实验,获得了米级定位精度。文献[8]通过伪卫星共享一个晶振时钟实现了基于载波观测值的星间单差单点定位,室内定位精度达到实时厘米级。文献[9]采用基于改进粒子群算法的模糊度函数法(Ambiguity Function Method,AFM)对室内异步伪卫星的模糊度进行单历元固定,提高了传统 AFM 的计算效率和搜索能力,并在单频软件接收机上实现了室内伪卫星厘米级的定位精度。文献[10]开发了一种新的伪卫星室内定位系统,发射机和接收机使用同一个时钟,并且伪卫星信号可以被通用接收机处理,仿真实验结果表明该系统可以实现米级定位精度。
上述研究通常忽略了多径效应对定位结果的影响,或采取硬件措施(如螺旋天线等)来抑制多径误差,系统成本过高,而对于异步伪卫星室内定位系统,接收机采样时间不同步带来的测距误差往往也被忽视。本文主要研究改善异步伪卫星定位系统算法性能的数据处理方法,通过中国电子科技集团第五十四研究所自主研发的伪卫星设备研究了钟漂和多径效应对定位产生的影响,并提出一种基于载噪比加权融合的伪卫星室内定位新方法。该方法能有效抑制上述误差,仅使用伪距观测值便能达到亚米级的定位精度,在深度室内环境中具有良好的应用前景。
1 异步伪卫星定位模型
1.1 观测方程
不同于 GNSS卫星安装了高精度原子钟,伪卫星钟一般使用低成本的温度补偿晶体振荡器,因此伪卫星钟很不稳定,无法做到彼此间时间同步,也就不能通过解观测方程来校准接收机钟差。为了消除伪卫星钟差和接收机钟差,通常采用相对定位的方式进行室内坐标解算。移动站和基准站的非差伪距观测方程分别为:

式中,和为移动/基准站对第i颗伪卫星的伪距观测值,和为移动/基准站到第i颗伪卫星的几何距离,c为光速,δti为第i颗伪卫星的钟差,δtrov和分别为移动站和基准站的接收机钟差,和分别为非建模误差及观测噪声。为消除伪卫星钟差,接收机间作单差可得如式(2)所示的观测方程:

式中,Δ为单差算子。同样地,为消除接收机钟差,对观测方程作星间单差可得伪距双差观测方程:

式中,∇Δ为双差算子。式(3)即为异步伪卫星室内定位观测方程。
上述方程成立的前提条件是基准站和移动站接收机必须保持严格的时间同步,即二者在相同的时间基准下产生观测值和时间戳,一般要求两台接收机的采样时间同步误差在1 μs之内。当接收机采样时间不同步时,伪卫星和接收机钟漂会导致伪距双差观测值振荡并偏离真实值,影响最终的定位结果。此外,室内多径和信号传播效应还会加剧这种采样时间不同步[7]。
1.2 随机模型
观测方程的随机模型能够更加合理地分配各观测方程在坐标解算中所起作用的大小,也能一定程度上抑制多径效应对定位结果的不利影响。在GNSS定位中,常用的随机模型主要有等权模型、基于卫星高度角的模型和基于载噪比或信噪比的模型。对于伪卫星室内定位,由于没有对流层和电离层误差,也不存在类似室外复杂环境中高大障碍物的遮挡,实际应用中,伪卫星一般静止安置在室内较高处,伪卫星的高度角对于信号质量的影响很小,因此,本文研究了等权模型和载噪比模型对于定位结果的影响。
等权模型假设各颗伪卫星的观测值误差符合相同的统计分布且互不相关,其权矩阵等于单位阵。在滤波过程中,观测噪声矩阵则设置为:

式中,I为单位阵,σ为观测值标准差。
载噪比模型根据接收机接收到的信号强弱来进行定权,一般来说,载噪比大小与伪卫星的信号质量成正比,载噪比越大,观测值的误差通常就越小。本文采用如下载噪比模型进行伪卫星室内定位实验:

式中,C0为常值,大小为1.1×104m2[11];C N0为载噪比,单位为dB·Hz。
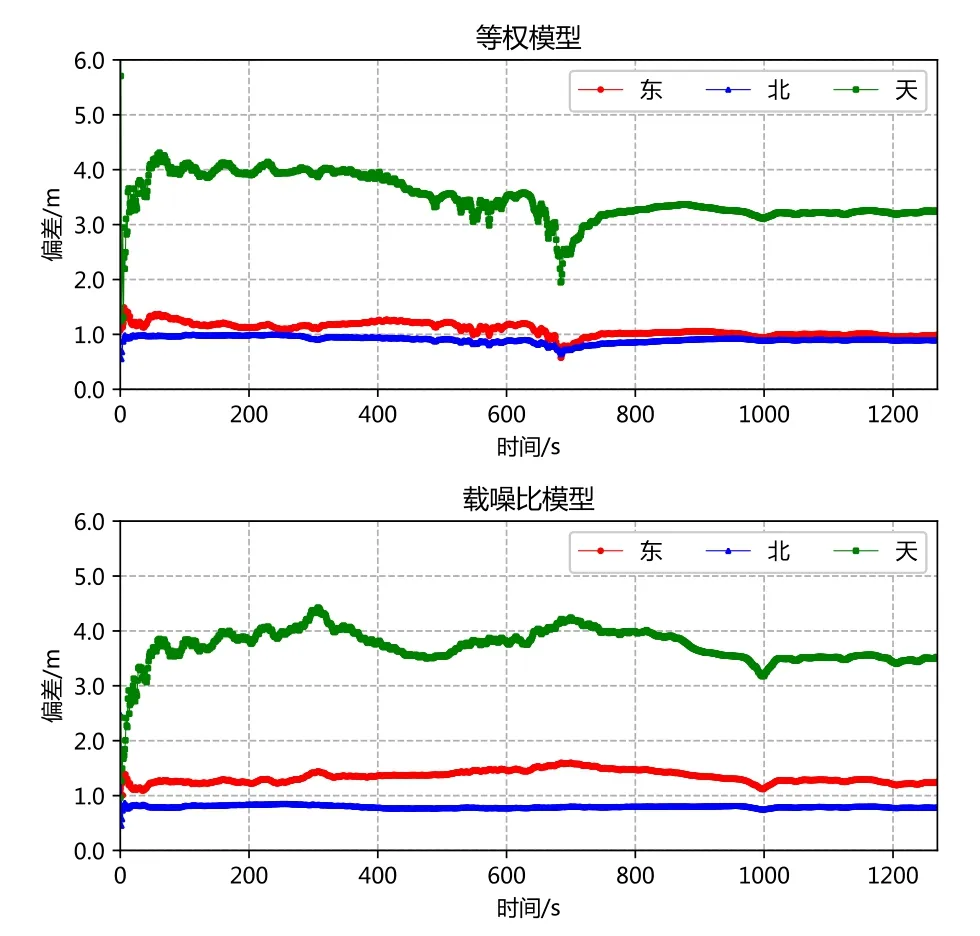
图1 基于不同随机模型的定位误差序列对比Fig.1 Comparison of positioning error series based on different stochastic models
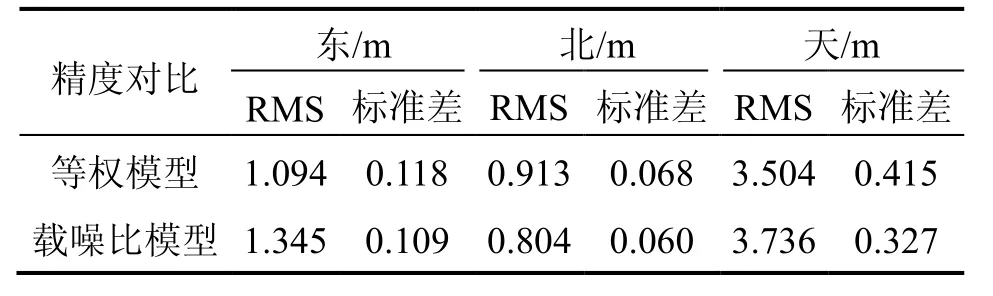
表1 基于不同随机模型的定位结果统计Tab.1 Positioning result statistics based on different stochastic models
图1为分别采用等权模型和载噪比模型进行室内静态点定位得到的误差序列,定位结果统计值如表1所示。可以看到,二者没有明显的差别,采用等权模型得到的定位误差均方根(Root Mean Square,RMS),在东、北、天三个方向上分别为1.094 m、0.913 m和3.504 m,而采用载噪比随机模型得到的定位误差RMS值则为1.345 m、0.804 m和3.736 m。载噪比随机模型在伪卫星室内定位中对定位精度没有明显的提升,究其原因,是由于受到多径及非视距(Non-Line of Sight,NLOS)信号的影响,室内环境较为复杂,单纯依赖载噪比的大小并不能确定接收机接收到的伪卫星信号类别及质量。考虑到二者整体效果相当且等权模型无需进行额外计算,一般基于等权模型进行接收机位置解算,本文将采取另外一种方式对载噪比信息加以利用。
2 载噪比加权融合定位算法
2.1 加权质心
质心算法的主要实现原理为:对未知节点接收附近锚节点的坐标信息求平均,获得锚节点的质心,该质心被视为未知节点所在的位置。在锚节点分布均匀且充足的情况下,可获得较高的定位精度。传统算法没有考虑各锚节点位置信息的权重,忽略了观测数据的不同影响力。为了提高定位精度,通常采用加权质心定位算法[12]。用户接收机的位置可由式(6)计算得到:
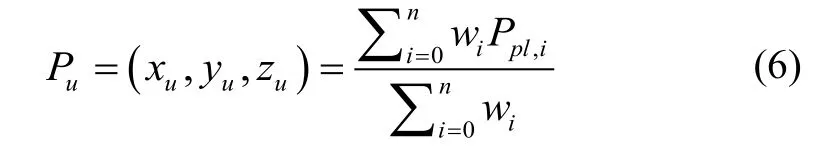
式中,Ppl,i为第i颗伪卫星的坐标向量;wi为相应的权重,决定了系统的定位精度。
定权的方式有许多种,核心都是利用未知节点和锚节点的距离来修正权值。本文中的权值由接收机接收到的伪卫星载噪比值计算得到,其表达式为[7]:

式(7)反映了从载噪比测量值到距离的一种变换。使用载噪比对质心算法定权的一个优点是,其在空旷无遮挡环境下和卫星高度角定权表现一样好,但在比较差的信号环境中拥有更好的性能[13],适合室内环境。此外,载噪比不受时钟同步问题的影响,避免了由于钟漂造成的测距误差。
2.2 基于伪距和载噪比的融合定位
质心算法的固有缺陷是其定位精度依赖锚节点分布情况和布设密度。伪卫星室内定位中,考虑到设备成本及功耗,一般较难通过增加伪卫星的数量来提升质心算法的定位精度。因此,在该方法基础之上引入新的观测量信息或定位模式,通过增加冗余观测值,进行观测值域的组合,可以提升定位的精度与可靠性。本文提出一种基于伪距和载噪比观测值的融合定位方式,联立式(3)和(6)得到新的观测方程:

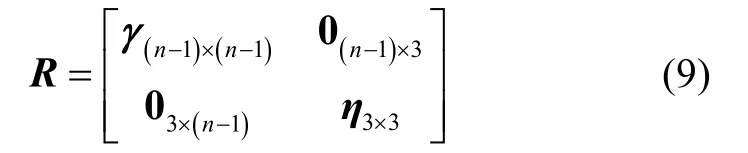
式中,γ、η分别为伪距和载噪比观测噪声误差矩阵,通过分析实际观测值的统计特性得到。
3 实验验证
3.1 数据来源
为了验证算法的可靠性,采集了约20 min的伪卫星静态观测数据,数据采样率为1 Hz,根据伪卫星的几何分布选取了两组不同的数据进行室内定位解算,并与传统定位方法进行对比。实验场地(约3m×5m)位于石家庄某测试场测试楼内,实验设备包括8颗自制伪卫星(4台发射机和8个贴片天线)、2台能接收伪卫星信号的u-blox商用接收机,以及1台用于存储测量值的笔记本电脑,伪卫星可调制播发GPS L1波段信号。8颗伪卫星分别放置在测试场地的四个角落,其中每两颗互相靠近。伪卫星和接收机的真实坐标事先由全站仪标定。实验场地与设备如图2所示。

图2 实验场地与设备Fig.2 Experimental site and equipment
3.2 实验一
为了全面评估定位算法的性能,首先采用全部 8颗伪卫星进行定位解算,以确保良好的伪卫星几何分布和充足的多余观测量,伪卫星与接收机的空间分布如图3所示,室内环境较为复杂。
图4为u-blox接收机采集的伪距双差观测值与真实伪卫星与接收机真实几何距离之间的偏差(参考星为2号伪卫星),可以看到,由于受到采样时间不同步以及多径和室内信号传播效应的影响,伪距双差观测值的质量比较差,存在随时间变化的振荡和偏差。短基线经过双差处理还会放大观测误差和噪声,这将导致定位结果严重偏离真实值,甚至发散。差矩阵。采用无迹卡尔曼滤波(Unscented Kalman Filter,UKF)进行定位解算,无需对上述方程进行线性化,利用确定的样本点来描述系统状态向量估计值的分布情况,可以削弱伪卫星定位的线性化误差[14]。
对于系统过程噪声方差矩阵Q和观测噪声方差矩阵R,由于是静态定位,Q设为零矩阵,将观测噪声方差矩阵表示为:

图3 伪卫星与接收机空间分布示意图Fig.3 Spatial distribution of pseudolites and receivers
图5为移动站接收机采集的伪卫星载噪比观测量,对比伪距双差观测值,静态观测的载噪比则相对稳定,适合作为观测信息参与室内定位解算。但由于接收机周围环境变化(如人员走动)以及一定程度的信号干扰,部分伪卫星信号的载噪比波动范围较大。

图4 伪距双差观测值与真实距离的偏差Fig.4 Deviation between pseudorange double difference and real distance

图5 移动站载噪比测量值Fig.5 C/N0 measurements of rover receiver

图6 实验一定位误差序列对比Fig.6 Comparison of positioning error series in experiment-1
定位结果的误差序列如图6所示,三种定位方法都采用了静态模式进行坐标解算。通过对比可以看到,采用融合定位方法的误差最小,且定位结果的稳定性较伪距双差定位得到了很大提升。由于钟漂、室内多径和信号传播效应的影响,伪距双差的定位误差较大,并且有轻微的发散趋势。采用加权质心方法的定位结果较伪距双差好,原因在于其较为稳定的载噪比观测输出、充足的伪卫星数量以及良好的伪卫星分布。
表2为三种方法的定位结果统计,融合定位方法的外符合、内符合精度分别达到了分米级和厘米级。和伪距双差定位相比,东方向、北方向的定位误差分别减小了 95.0%和 98.5%;相较于加权质心法,东方向、北方向的定位误差分别减小了75.4%和96.5%。

表2 实验一定位结果对比Tab.2 Comparison of positioning results in experiment 1
3.3 实验二
本实验选取了1、2、3、4和8号伪卫星的观测数据进行了室内定位解算,该场景中伪卫星的几何分布较差,能更好地体现本文算法的优势。定位误差序列如图7所示,可以看到,采用融合定位方法得到的定位结果精度最好,平面误差都在1 m以内。如表3所示,融合定位方法的外符合、内符合精度分别达到了亚米级和厘米级,与伪距双差定位相比,东方向、北方向的定位误差分别减小了55.4%和81.1%;相较于加权质心法,东方向、北方向的定位误差分别减小了33.3%和25.7%。
通过本实验可以发现,采用融合定位的方法在伪卫星几何分布较差的情况下对定位精度的也有着显著的提升,因此该方法能适用于观测环境较差的室内场景,在原有伪距观测值的基础上通过增加新的观测信息(载噪比)使定位方程更加稳定,有效抑制了由于伪卫星几何分布不佳造成的定位精度的下降。
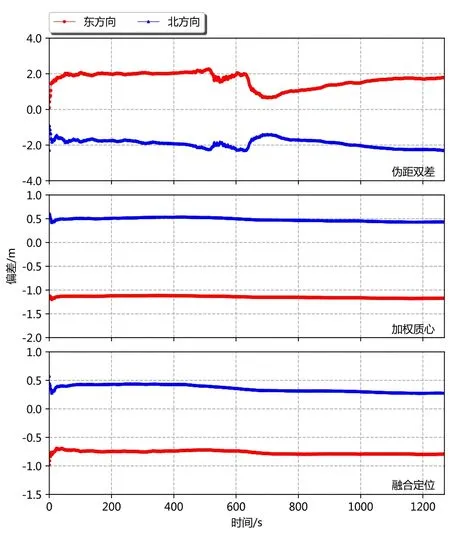
图7 实验二定位误差序列对比Fig.7 Comparison of positioning error series in experiment 2
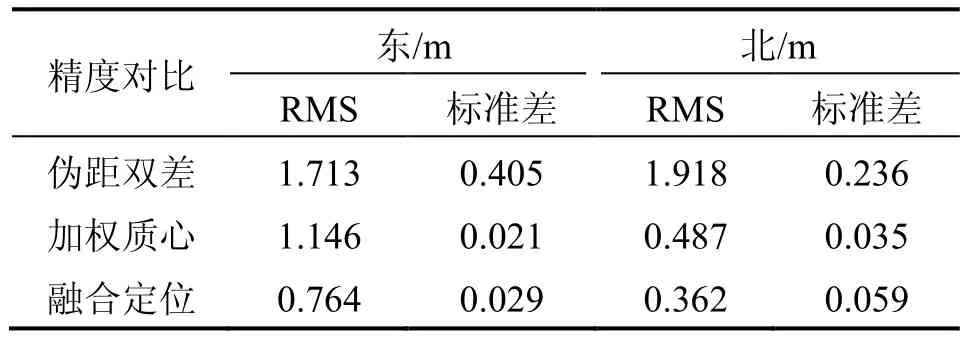
表3 实验二定位结果对比Tab.3 Comparison of positioning results in experiment 2
4 结 论
针对异步伪卫星室内定位受钟漂与多径效应影响而无法准确定位的难点,本文提出了一种基于观测值域的伪距与载噪比融合的伪卫星室内定位新方法,并采用伪卫星实测数据对算法的性能进行了验证。
实验中分别讨论了两种不同场景使用该方法对室内定位精度的提升,结果表明:1)融合定位方法充分利用了伪距和载噪比观测信息,定位的精度优于伪距双差和加权质心法定位,东方向和北方向的定位精度分别达到了0.131 m和0.036 m;2)该方法在伪卫星几何分布较差的环境中也有很好的定位效果,东方向和北方向的定位精度分别为0.764 m和0.362 m,且具有一定的抗粗差性能,适用于深度室内场景。在后续的研究中,将进行复杂室内场景大范围、连续动态定位实验,进一步优化定位算法,提升算法的鲁棒性。

