一种基于双差观测的BDS 周跳探测与修复方法

谢瑞煜，杨利斌，赵建军

（海军航空大学，山东 烟台 264001）

0 引言

在接收以载波相位为观测值的卫星信号时，接收机必须始终保持对卫星信号的跟踪，在不出现中断（失锁）下，接收机就会不断将载波相位的变化情况记录下来。但有时接收机因为一些原因，不得不在卫星信号容易受遮挡或无线电受干扰的地方进行接收，接收的信号会发生短暂中断，这使得观测值的相位周数产生跳变，这种现象称为周跳［1-2］。在发生周跳现象后，尽管接收机及时恢复对卫星信号的跟踪观测，不影响获取所测相位的小数部分正确值，但整周数会随着信号中断而发生偏差，结果使载波相位的观测值不正确［4］。而且，周跳具有继承性，不仅影响当前历元的相位观测值，还会使该历元后的相位观测值均受到同样的整周数跳变的影响。

现代定位对精度的要求与日俱增，载波相位周跳是高精度定位中一项重要影响因素。为了克服这一影响，探测并修复相位周跳成为观测值处理中的一项重要难题。距今为止，周跳探测修复手段多种多样，在不同的定位情况和条件下，高次差法、多项式拟合法、小波变换法、MW 组合法均得到了广泛的应用［5-6］。

除了观测值的处理，观测方式的不同对周跳探测修复存在较大的影响。在相对定位中，因为选取不同观测站，不同的卫星和不同的观测历元情况下，卫星的轨道误差、接收机钟差及电离层和对流层的折射误差对观测值的影响不同。因此，利用这些观测值的不同组合进行相对定位，便可有效地消除或减弱上述误差的影响，从而可以更好地对周跳进行探测［3］。

1 基于双差观测值的高次差法

1.1 原始高次差法

原始高次差法是通过相邻两个观测值间依次求差得到一次差，再利用相邻的两个一次差得到二次差，同样道理，三次差、四次差接连得到，从而使观测值的变化逐渐变小；如果观测值里面没有周跳发生，三次差、四次差得到的数值将趋近于零，否则，得到的数值中就会产生较大数。通过采用这样的方法，可以探测某历元时发生的周跳［7-8］。

原始高次差法虽然简单易操作，但是发生小至1 周的小周跳时，钟差、大气延迟误差等各种误差将使高次差法无法正常使用，因而在这里采用基于双差观测值的高次差法进行探测周跳。

1.2 改进高次差法

在选择单差、双差、三差时，虽然三差能最大限度地消除整周未知数影响，但观测方程数量太少，使得最后的定位误差大大增加；同时单差消除误差有限，因此，采用双差观测方程最为适合［9］。

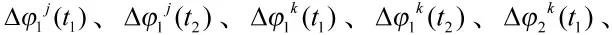
其中，观测量方程的一般形式为：

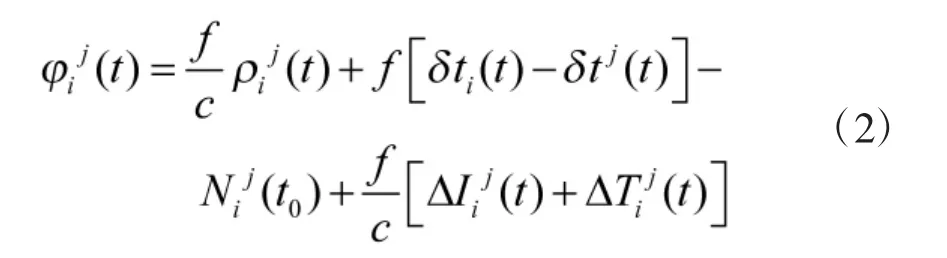
不同观测站，同步观测相同卫星所得观测量之差即为单差，其表达式为：

不同观测站，同步观测同一组卫星所得单差之差即为双差，其表达式为：

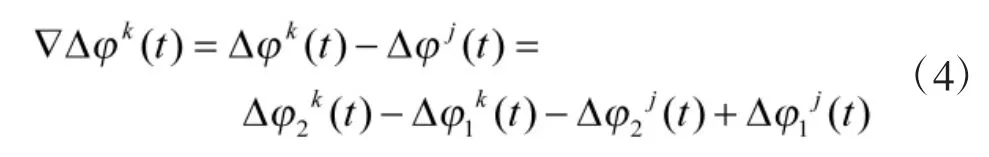
将式（2）应用于观测站T1、T2，带入式（3），并忽略电离层残差影响，可得到简化单差观测方程：

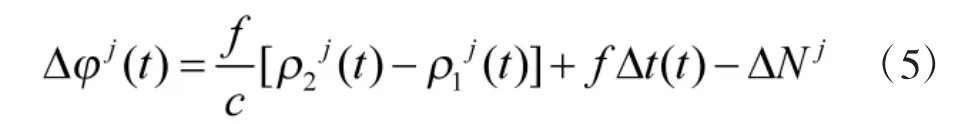
式（5）中：

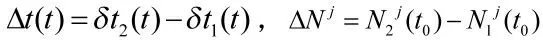
若取

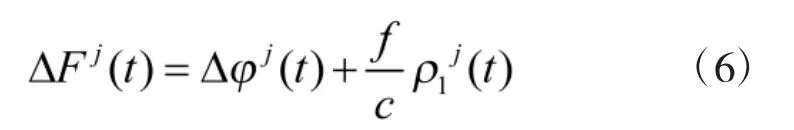
则单差观测方程可改写成：

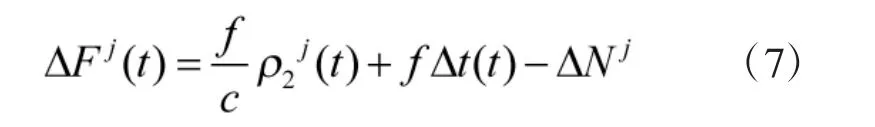
将式（7）应用于T1、T2两观测站和sj、sk两颗同步卫星，并忽略大气折射残差影响［10］，可得到双差观测方程：

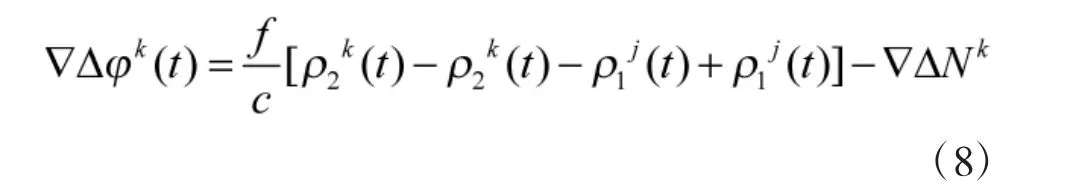
若取观测站T1作为已知参考点，并取

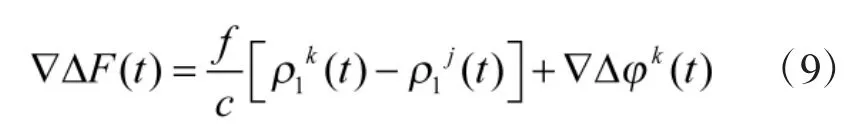
则双差观测方程为：

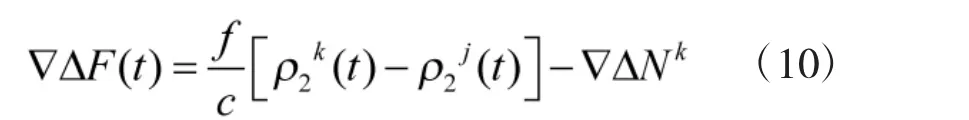
选定观测值后，对现有观测值重复高次差法。一般情况下，原始载波相位观测值数值在千万到上亿数量级不等，进行双差后，观测值减小，对小周跳探测更有利。

2 最小二乘多项式推估法

设y0，y1，…，yn-1为获取的观测量序列，y 为观测量的最佳估计［11-12］，则多项式拟合表示为：

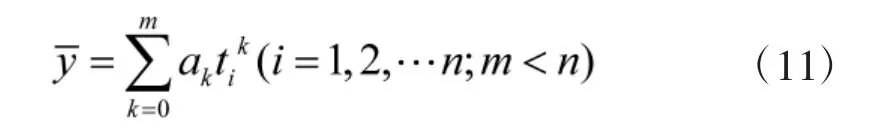
式中，m 为多项式的拟合阶数；ti为历元观测时间。

设vi为yi的观测值残差，则拟合的观测方程为

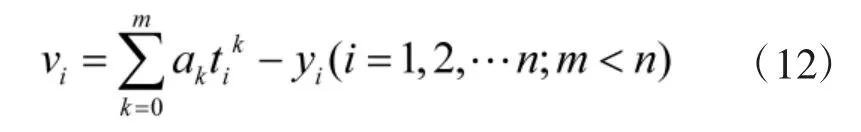
表达为矩阵则为

上式等价于

第n+1 个历元的外推相位估计为

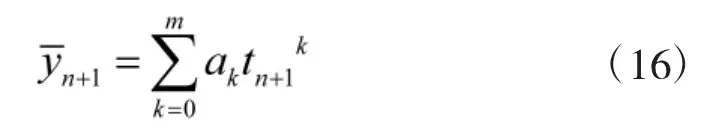
3 探测与修复方案

首先将n 个双差相位序列读入，一方面进行高次差法计算，通过残差分析，判断是否超限，如果不超限，则周跳检测通过，如果超限，则标记超限时的历元位置。在另一方面，同时进行基于最小二乘的多项式法拟合计算，推估后的结果与当前双差读入值比对，判断是否有超限，为了检测出小周跳，该结果联合高次差法已判断出的周跳位置，对所有周跳位置根据差值进行推估修复，从而得到一个连续的观测相位值［13］。

4 算例分析

图1 周跳处理流程

实测一组B1频点载波相位观测值，取200 个历元，采样间隔为1 s。人为在第39、98、139 个历元上加入0.2 周、3 周、-0.2 周周跳。因为在采样时采用高采样率观测数据，所以星地距离对时间的四阶五阶导数已趋于无穷小，所以拟合阶数取m=3；同时拟合窗宽度加大，在提高外推值精确性的同时，计算量也加大，在保证精度的情况下，宽度值采用n=5［14］。实验在MATLAB 平台进行仿真运算。

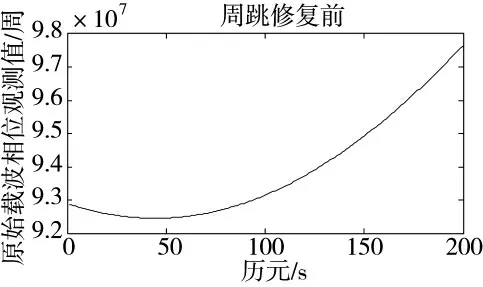
图2 周跳修复前原始观测值曲线

在图2 中原始载波相位观测值曲线上，加入周跳后无法直接寻找周跳发生位置。

对比是否用双差观测值来进行周跳探测，将两者进行对比：

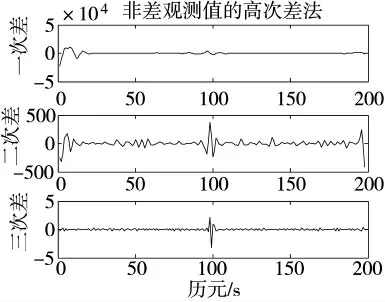
图3 非差观测值的高次差法

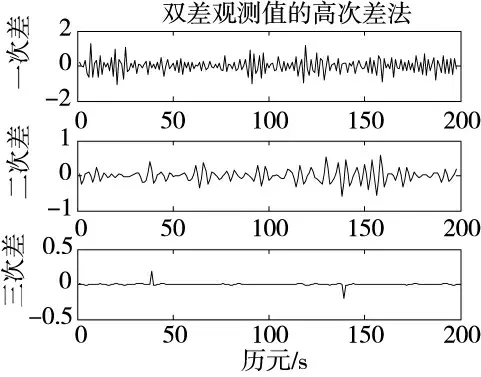
图4 双差载波相位高次差法

图3 中经过3 次差后，在第98 个周跳上曲线抖动较大，此位置即为周跳发生位置。但是在第39和第139 历元上的小周跳无法探测出来，说明非差观测值在发生小周跳时，无法有效探测。考虑到B1频点载波相位的频率为1 561.098 MHz，假设该接收机钟的短期稳定度为5×10-10，采样间隔为1 s，所以接收机钟的随机误差将对探测所造成的影响达到1 s×5×10-10×1 561.098 Hz=0.78 周，接受机误差盖过周跳误差，因此，无法探测。

图4 中，在使用双差后，观测值中消除了接收机钟差、卫星钟差、电离层对流层延迟等各种误差，第39 和第139 历元上的小周跳得以有效探测。

取39 周跳前5 个观测值，经过拟合计算得到多项式方程为y=3.130 9+0.088 4t-0.002 5t2+0.000 0t3，代入t=39，得y=3.921 3，3σ=0.24，差值小于3σ。此时，在多项式法无法有效探测时，用改进高次差法探测，则可以弥补多项式在探测周跳上的缺点。同样方法，在第139 历元上，可以联合两种方法，先用改进高次差法探测小周跳，然后用多项式推估法进行小周跳修复。

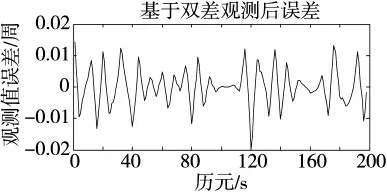
图5 基于双差观测后的误差曲线

图6 基于双差观测值的周跳修复前后的观测值曲线

5 结论

周跳探测与修复是高精度定位领域一项重要的内容，针对一般的高次差法和多项式拟合法无法探测到小至1 周的小周跳情况，文中经过仿真计算，得到结论1：在对比是否通过双差观测值进行高次差法计算后，非差观测值受到各种影响只能探测大周跳，而基于双差观测值高次差法能有效探测出小周跳；结论2：应用基于最小二乘的多项式拟合推估方法后，小周跳得以修复。

通过改进周跳探测与修复方法后，观测值记录得以连续，这为后期进行整周模糊度的解算奠定了良好的基础。