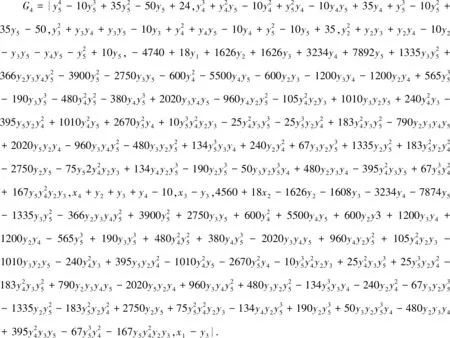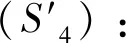图的k-全染色问题与Gröbner基求解
(1.海南大学理学院数学系,海口,570228;2.广东财经大学统计与数学学院,广州,510320;3.海南熊大教育咨询有限公司,海口,570220)
1 引言
在图的全染色(Total coloring)问题研究中,熟知的TCC猜想是,最大度为Δ的每个有限图都是(Δ+2)-全可染的([1],[2],[3]). 目前该猜想的研究已经取得了一系列成果(参见[4]-[11] ). 对于任意给定的有限图G和任一正整数k,本文证明G的k-全可染问题等价于一个多元多项式方程组在{1,2,…,k}范围的求解问题. 注意到一个多元多项式方程组在{1,2,…,k}范围的解(如果存在的话)只有有限多个, 根据熟知的Gröbner基算法理论, 我们就可通过计算出一个特殊的Gröbner基给出一个图k-全可染的有效判别与求解途径, 进而求得图的全染色数χ″(G).由于多项式的Gröbner基的计算技术如今已经非常成熟,使用诸如Maple, Macaulay, CoCoA等其中任何一个计算代数程序都可计算出由给定多项式组确定的理想的Gröbner基,况且目前更有像F4, F5这些最新发展的快速计算Gröbner基的算法面世. 因此,本文得到的方法可直接有效地应用于任何一个有限图,从而为TCC猜想的研究提供有效的帮助.
本文中考虑的图为任意有限图.
2 图的k-全染色与多元多项式方程组的解
本节中图的全染色的基本概念参见[4]. 有关一般图论的基本理论见[1],[2].
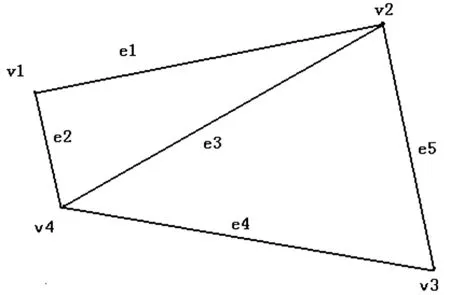
给定图G=(V,E), 其中V={v1,…,vn}是G的顶点集,E={e1,…,em}是G的边集.
定义1若能用k种颜色给集合V∪E中的元素进行染色,使得其中任意一对相邻或相关联的元素接受不同的颜色, 则称这个图是k-全可染的.
定义2若图G是k-全可染的,且不存在k′(k′ 对于图G, 我们对其顶点和边k-染色的不同方案引入向量(X,Y)k=(x1,x2,…,xn,y1,y2,…,ym)T,其中 按照k-全染色的定义我们知道每个顶点、每条边的染色方案有k种, 也即对于图G中的任何一个顶点、任一条边,按照向量分量的定义,xi,yj的取值为{1,2,…,k}中的一个, 也即xi,yj的取值是分别是方程 (xi-1)(xi-2)…(xi-k)=0,i=1,2,…,n, (2.1) (yj-1)(yj-2)…(yj-k)=0,j=1,2,…,m (2.2) 的根.因为相邻的顶点不能染相同的颜色, 故对任意一对相邻顶点vi与vs,它们的染色分别为xi和xs,满足|xi-xs|≥1. 这就表明|xi-xs|的取值为{1,2,…,k-1}中的一个, 也即xi,xs的取值是方程 (|xi-xs|-1)(|xi-xs|-2)…(|xi-xs|-(k-1))=0 的根. 直接验证可知上面的方程等价于多项式方程 ((xi-xs)2-12)((xi-xs)2-22)…((xi-xs)2-(k-1)2)=0. (2.3) 又因为相邻的边也不能染相同的颜色, 故对任意一对相邻边ej与et, 它们的染色分别为yj和yt, 满足|yj-yt|≥1. 这就表明|yj-yt|的取值为{1,2,…,k-1}中的一个, 也即yj,yt的取值是方程 (|yj-yt|-1)(|yj-yt|-2)…(|yj-yt|-(k-1))=0 的根. 直接验证可知上面的方程等价于多项式方程 ((yj-yt)2-12)((yj-yt)2-22)…((yj-yt)2-(k-1)2)=0. (2.4) 对相关联的元素不能染相同的颜色,故对任意一对相关联的顶点vi与边ej,对应的染色为xi和yj, 满足|xi-yj|≥1. 这就表明|xi-yj|的取值为{1,2,…,k-1}中的一个, 也即xi,yj的取值是方程 (|xi-yj|-1)(|xi-yj|-2)…(|xi-yj|-(k-1))=0 的根. 直接验证可知上面的方程等价于多项式方程 ((xi-yj)2-12)((xi-yj)2-22)…((xi-yj)2-(k-1)2)=0. (2.5) 综合式(2.1)-(2.5),我们得到关于x1,x2,…,xn,y1,y2,…,ym的多元多项式方程组 下面的定理给出方程组(Sk)的解与图G的k-全染色方案的对应关系. 定理1方程组(Sk)每个解对应图G的一个k-全染色;反之亦然,且该对应是一一对应. 证明“⟹” 取方程组(Sk)的任意一个解,记作(X,Y)0=(x1,x2,…,xn,y1,y2,…,ym)T. (X,Y)0是方程组的解, 也就是方程(2.1)-(2.5)的根, 故由k-全染色的定义知道该解对应一个k-全染色方案,即对x1,x2,…,xn,y1,y2,…,ym的取值进行分类, 取值相同的归于一类,染一种颜色. 因为有k种不同的取值, 也就能得到k类,染k种不同的颜色. 按此分类染色就可得到一个k-全染色方案. “⟸” 取图G的一个k-全染色方案, 记{1,2,…,k}为该k种染色对应的取值. 因为k-全染色中相邻元素和相关联元素不能染相同的颜色, 故该染色方案对应的染色向量(X,Y)1=(x1,x2,…,xn,y1,y2,…,ym)T是分别满足方程(2.1)-(2.5)的, 也即满足方程组(Sk),从而染色向量(X,Y)1是方程组(Sk)的一个解. 容易看出以上给出的对应是既单且满的. 给定具有n个顶点、m条边的图G=(V,E),G显然有极小全染色. 但是对于任意一个1≤k≤|V|+|E|=n+m,一个自然的问题是:G是否有含k种颜色的全染色方案?上节中我们证明了图G的k-全染色方案的存在问题完全等价于一个多元多项式方程组在{0,1,2,…,k}范围的求解问题, 且由定理 1 可知存在图G的k-全染色方案的集合与多元多项式方程组(Sk)的解的集合之间的一个一一对应. 本节中我们用经典的判别多项式方程组解的存在性的Gröbner基方法(参见[3])来给出G是否为k-全可染的一个有效判别. 定理2对于给定的k, 其中1≤k≤|V|+|E|=n+m, 考察下面由复数域C上多项式确定的方程组: (1)图G是k-全可染得当且仅当方程组 (Sk) 有解. (2)若方程组 (Sk) 有解, 则 (Sk) 的所有解给出G的所有k-全染色方案. (3)令I是方程组 (Sk) 中方程左端多项式在多元多项式环R=C[x1,…,xn]中生成的理想. 则方程组(Sk)有解当且仅当理想I的Gröbner基不含非零常数. 证明(1)由定理 1 知图G=(V,E)有k-全染色方案当且仅当方程组(Sk)有解. (2)由定理1与上面(1), 该结论是显然的. (3)由于方程组(Sk)解的存在性与理想I的Gröbner基给出的方程组的解的存在性是等价的,而C是代数闭域, 因此该结论由著名的Hilbert零点定理与熟知的Gröbner基的性质([3])即可得到. 本节根据第三节定理 2 给出求图的k-全染色、极小全可染方案及全可染色数χ″(G)的Gröbner基方法. 根据前面的讨论, 在方程组(Sk)有解的情况下, 只要解方程组(Sk)即可得到图G的所有k-全可染方案. 求解多元多项式的方法虽然很多, 但是注意到方程组(Sk)如果有解, 则它的坐标的取值范围是{1,2,…,k}且解的个数一定是有限的. 这样, 由[3]可知, 在某个消元单项式序下, 例如在单项式序 x1≻x2≻…≻xn-1≻xn≻y1≻y2≻…≻ym-1≻ym 下理想I的一个约化Gröbner基给出与方程组(Sk)等价的方程组为: 一个图的k-全可染色方案(如果存在的话)不一定是唯一的. 但由于每个有限图中顶点个数和边数之和是有限的, 故k-全可染的染色数k有最小值, 而该最小值就是该图的全可染色数χ″(G). 以下我们根据定理2给出求图G的全可染色数χ″(G)的一种方法. 定理3k是图G的全可染色数χ″(G)当且仅当方程组(Sk)有解而方程组(Sk-1)无解. 证明“⟹” 若k是图G的全可染色数χ″(G), 则说明图G全染色方案中包含k种颜色的染色方案, 由定理2(1)的结论我们得知方程组(Sk)有解; 而由全可染色数的定义, 图G中全染色方案中包含的染色颜色数最少为k, 故图G中不存在颜色数为k-1的全染色, 所以方程组(Sk-1)无解. “⟸” 若方程组(Sk)有解而方程组(Sk-1)无解, 由定理 2(1)的结论知,图G是k-全可染的,但不是(k-1)-全可染的, 也就说明图G中全可染方案所包含的颜色数最小只能为k, 因此根据全可染色数的定义k是图G的全可染色数χ″(G). 由定理3可以得到一个全可染色数χ″(G)的一个解决方案, 即我们可以通过采用由小到大的次序计算图的全可染色数χ″(G), 进而得到图G的极小全可染色方案. 最后,我们给出一个实际例子来说明上节给出的方法的有效性. 考察有限图G=(V,E), 其中顶点集V={v1,v2,v3,v4}, 边集E={e1,e2,e3,e4,e5}. 图1 以下我们应用前面得到的计算方法来分别计算图G的k-全可染、极小全可染色数以及极小全可染方案. 对k采用从大到小的次序来计算k-全可染(k>1): 2-全可染情形: 通过MAPLE计算Gröbner基的程序计算得到理想IS2的一个约化Gröbner基:G2={1},包含非零常数, 所以由定理2(3)的结论知方程组(S2)是无解的, 故该图不存在2-全染色. 3-全可染情形: 通过MAPLE计算Gröbner基的程序计算得到理想IS3的一个约化Gröbner基:G2={1}, 包含非零常数, 所以由定理2(3)的结论知方程组(S3)是无解的, 故该图也不存在3-全染色. 4-全可染情形: 通过MAPLE计算Gröbner基的程序计算得到理想IS4的一个约化Gröbner基: 方程组(S4)有解而方程组(S3)无解, 由定理3的结论知图G的全染色数χ″(G)为4. 所有的4-全染色就是该图的极小全染色方案. 作者衷心感谢李会师教授的指导和帮助.3 图的k-全染色存在性的Gröbner基判别
4 求图的k-全染色方案, 全可染色数及极小全可染方案的Gröbner基方法
4.1 求图的k-全染色方案的计算方法
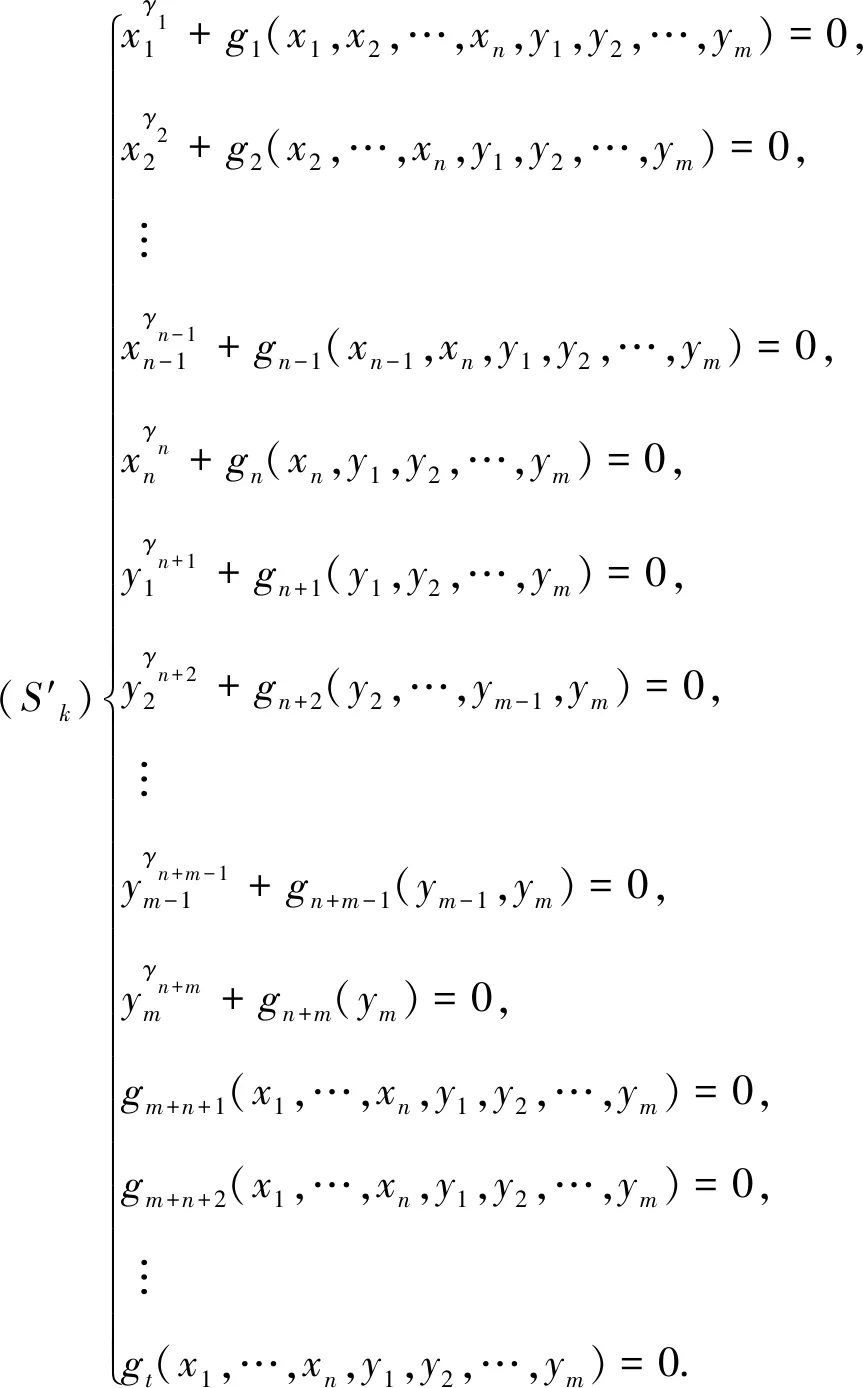
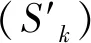
4.2 求图的全可染色数及极小全可染方案的计算方法
5 一个计算实例