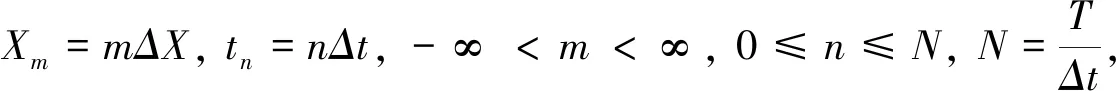体制转换市场中股价服从带门限均值回复过程的期权定价
(上海理工大学理学院,上海,200093)
1 引言
期权定价理论在金融资产定价问题相中最为重要的理论,且已取得了丰硕的研究成果.近年来,大量学者开始关注体制转换问题,并将其应用到金融研究的很多领域中.体制转换模型最早源于上世纪八十年代后期,Hamilton[1]首次将体制转换模型应用到金融计量经济学领域,并对美国经济周期进行了分析,发现美国GNP趋势函数的增长率会依据一类马尔可夫过程在不同状态之间转换.受文献[1]的影响,大量研究人员使用“马尔科夫调制”为结构变化建模,并进行研究.Buffington等[2]给出了体制转换模型下欧式期权满足的方程,却未给出具体解法.Zhou[3]利用热核方法给出了欧式看涨期权定价的近似解. Bufington等[4]对美式期权的定价进行研究,并给出精确解.但以上文章均只考虑了股价服从经典几何布朗运动的情况,极少有研究马氏利率下标的资产满足其它模型的期权定价,更没有考虑股价含有门限的情况.本文主要是研究股价服从带门限均值回复过程而折现率含有状态切换的情况下的欧式看涨期权进行定价问题.
2 股价过程
在风险中性测度Q下,股价为S(t),其对数X(t)满足如下随机方程:
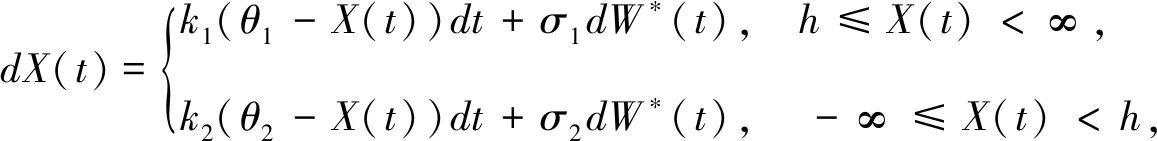
(2.1)
其中,W*(t)为布朗运动,h为门限,ki,θi,σi为已知参数.假设银行利率r由有限状态空间的Markov链{Y(t)}t∈T描述. 参考Elliott[5],令
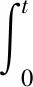
(2.2)
其中,A为转移矩阵,<,>为内积,M={M(t),t≥0}是关于Y生成的代数域的鞅.
3 期权定价
本节分三步对定价问题进行分析.首先对恒定利率下股价服从无门限的均值回复过程的期权定价进行研究,给出欧式看涨期权定价的近似解;再对体制转换市场下股价服从无门限的均值回复过程的期权定价进行研究,给出转换市场存在两个状态下的股价服从无门限均值回复过程的欧式看涨期权的近似解;在此基础上,最后研究转换市场存在两个状态下的股价服从带门限的均值回复过程的欧式看涨期权的近似解.
3.1 无门限的均值回复期权定价
在风险中性测度Q下,股价为S(t),其对数X(t)满足如下随机方程:
dX(t)=k(θ-X(t))dt+σdW*(t),
(3.1)
其中,W*(t)为布朗运动,k,θ,σ为已知参数.
定理1假设股价过程服从(3.1),银行利率恒为ri下的欧式看涨期权定价公式为:
其中
上式中的系数A1i,A2i,B1i,B2i可由注1得到.
证明在风险中性世界,欧式看涨期权定价公式为:
V0i(X,t)=V0(X,t,T,ei)=E[e-ri(T-t)(eX-K)+].
由Shreve[6]中费曼-卡茨公式知,V0i(X,t)适合以下定解问题:
令V0i(X,t)=f0i(X,τ),τ=T-t.则

边界条件为:
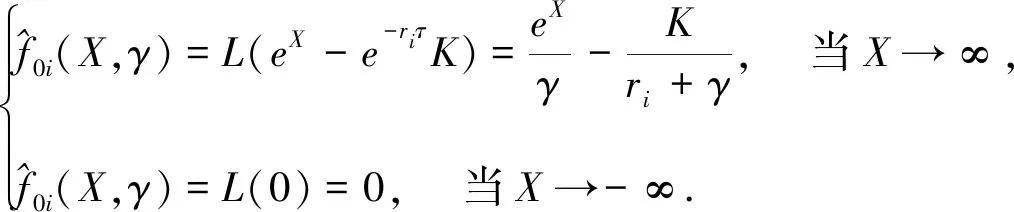
(3.2)
令
则当X≤κ时,上式可转化为如下库默方程:
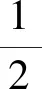
且有Lebedev[8]中的超几何函数性质:
其中
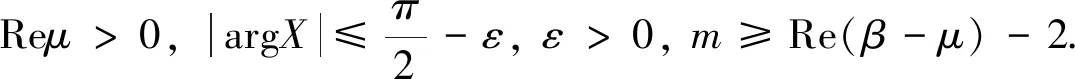
所以当X≤κ时,其解的形式为:
(3.3)
当X>κ时,其解的形式为:
(3.4)

其中W(·)为朗斯基行列式,
但由Wong等[9]知道有一个如下形式的特解:
其中
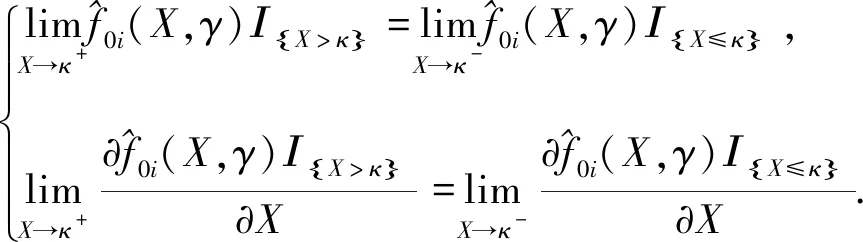
(3.5)
式(3.3),(3.4)中的系数A1i,A2i,B1i,B2i可由边界条件(3.2)和平滑性(3.5)确定.证毕.
注1参考了Chi Z等[10]中对定理1的证明方法,将式(3.3),(3.4)代入式(3.2)和(3.5)中,即可确定参数A1i,A2i,B1i,B2i:
3.2 体制转换市场下无门限的均值回复期权定价
定义1Gi(X,t;ξ,T)称为是该方程的基本解,如果它适合以下定解问题:
其中-∞ 为了给出Gi(X,t;ξ,T)的表达式,令u(X,t)=fpi(X,τ),τ=T-t.则 与定理1中求特解的方法类似,可得: 其中 定理2假设股价过程服从(3-1),银行利率服从状态空间为{1,2,…,n}的马尔科夫链Y(t).若ci(X,t)=c(X,t,T,ei)为状态模式i下的期权价格,则其满足如下方程: 其中,c(X,t,T,Y(t))=(c(X,t,T,e1),c(X,t,T,e2)…,c(X,t,T,en))′. 证明在风险中性世界,欧式看涨期权的定价(参见文献[4])为: 为推导出c(X,t,T,Y),先假设: (3.6) 则 其中Ψt=σ{X(u),Y(u);u≤t},显然V(t,X,T,Y)是关于Ψt的鞅.记 V(X,t,T,Y)=(V(X,t,T,e1),V(X,t,T,e2),…,V(X,t,T,en))′. 则 V(X(t),t,T,Y)={V(X(t),t,T,Y(t))}t∈T. 又由dY(t)=AY(t)dt+dM(t)和V(t,X,T,Y)的鞅性可得: 又由(3.6)可得: 因此 故 (3.7) 证毕. i=1,2.j=1,2. 且i≠j. 证明由(3.7)式知,状态模式i下的期权价格ci(X,t),i=1,2.满足如下方程 (3.8) 其终止条件为ci(X,T)=(eX-K)+,i=1,2.现参考姜礼尚[11],推导其解的形式.令 u(X,t)=ci(X,t)-Vi0(X,t),i=1,2, (3.9) 其中 Vi0(X,t)=e-λi(T-t)V0i(X,t),i=1,2. (3.10) 将(3.9)代入(3.8)得到: (3.11) 其终止条件为ui(X,T)=0,i=1,2. 由定义1可得到方程 的基本解为Gi(X,t;ξ,T).利用基本解Gi(X,t;ξ,T),方程组(3.11)可以转换为以下等价Volterra积分方程组: (3.12) 其中 (3.13) 将(3.12)中u1(X,t),u2(X,t)互相代入可得到: (3.14) 其中 通过迭代,积分方程组(3.14)的解可表示为: (3.15) 由于λ1,λ2一般是小量,因此可以略去λ1,λ2的2阶以上的小量.于是,由式(3.9),(3.10),(3.13)以及(3.15)可得到: ci(X,t)=ui(X,t)+Vi0(X,t)≈fi(X,t)+Vi0(X,t) i,j=1,2 且i≠j. 证毕. 注2由近似解可以看出,如果市场不存在体制转换,即λi=0,此时结果与定理1中的结论保持一致. i,j=1,2且i≠j, 其中 上式中的系数Ai11,Ai12,Ai21,Ai22,Bi1和Bi2可由注3确定. 证明当X 由定理3可得 (3.16) 的基本解.由定义1知 其中 同理当X≥h时,由定理2知 由定理3知 (3.17) 的基本解,由定义1知 再由边界条件和期权价格在h,κ处的平滑性条件,即可解得系数.证毕. 注3上述的边界条件为: 在h处的平滑性: 在κ处的平滑性: 因此,定理4中的系数Ai11,Ai12,Ai21,Ai22,Bi1和Bi2可由如下方程组确定: 在上一节中我们得到了体制转换市场下股价服从带门限均值回复过程的期权定价的近似解. 但若在现实中进行模拟操作会异常复杂.为实现模拟过程,现给出体制转换市场下带门限均值回复过程的期权定价的差分格式(参考姜礼尚[12]). 最终解得: 其中 记h=nhΔX,当m≤nh时,只需参数k由k1→k2,参数θ由θ1→θ2,参数σ由σ1→σ2即可.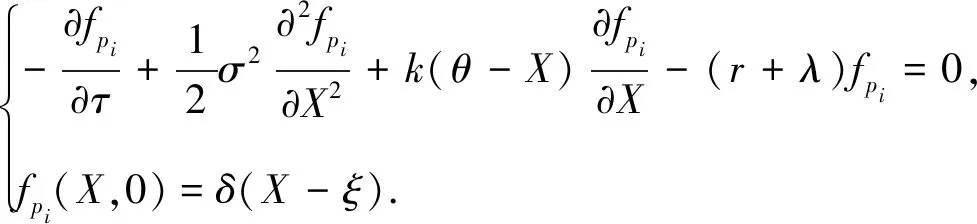
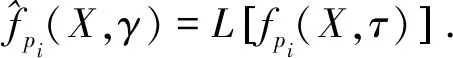
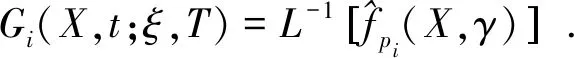
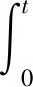
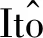
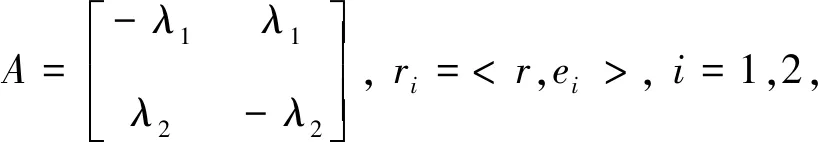

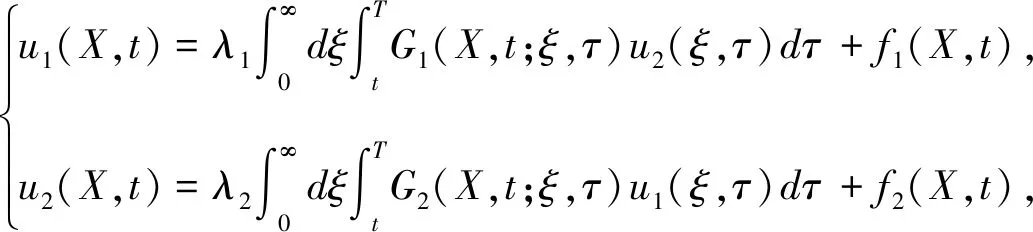
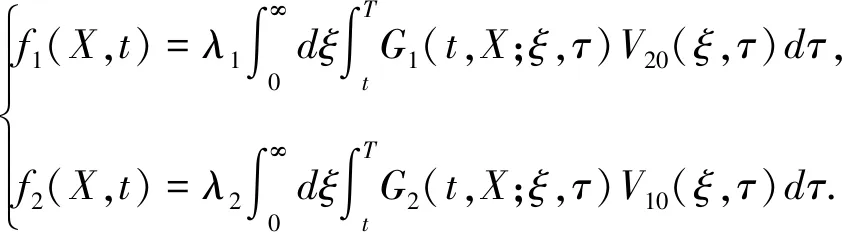
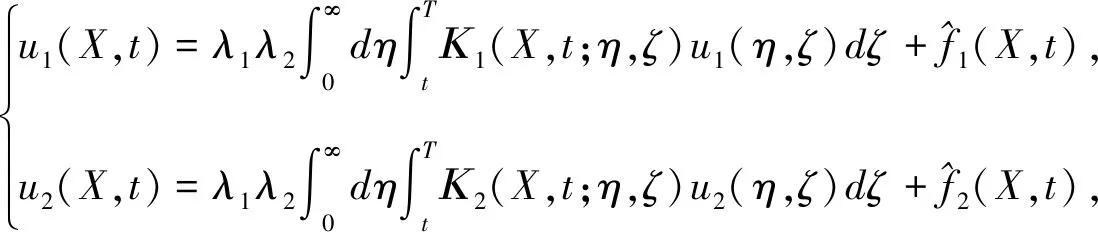
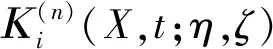
3.3 体制转换市场下带门限的均值回复欧式看涨期权
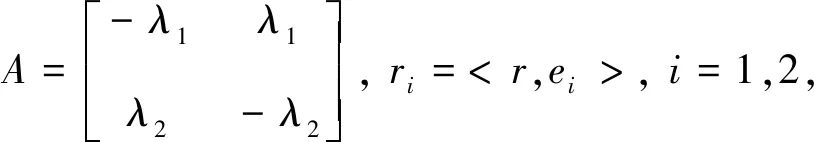
4 期权定价的差分格式