稳健的惩罚经验似然方法及压缩估计

(上海理工大学理学院，上海，200093)

1 引言

随着科学技术的不断发展，数据收集与处理的要求也日益提升.由于数据的来源之广和数量的不断积累，数据的结构越来越复杂，维数也越来越高.如何从海量的数据中快速高效的筛选并提取有价值的信息是我们值得研究和解决的问题.在统计学中，我们习惯的称研究目标为响应变量，收集到的相关信息为解释变量.变量之间的联系具有普遍性，一般是借助统计模型推断.线性回归模型是研究变量之间相互关系的一种有效工具，但当统计模型中有较多的变量时，如果选择的变量较少，就会发生变量的缺失导致模型会产生有偏差的估计和预测.为了避免这种困境，我们通常会选择相对较多的自变量.但是自变量的过多又会产生模型的过度拟合而影响参数估计和预测的效率，因此变量选择是统计模型和知识发现领域非常重要的课题之一.随着高维数据分析需求的日益增加，这一问题的研究显得更加突出而具有现实意义.

自20世纪六十年代以来，变量选择一直是统计模型推断的研究课题之一，许多文献对其进行了详细的研究.传统的变量选择有Akaike[1]在熵的概念上提供权衡估计模型复杂度和拟合数据优良性的标准AIC.从一组可供选择的模型中选择最佳模型时，通常选择AIC值最小的变量子集.Schwarz[2]提出了BIC的变量选择方法. BIC准则与AIC准则相似，都用于模型选择，但在惩罚力度上，BIC的惩罚项比AIC的大.在样本数量过多时，BIC准则可有效防止模型精度过高而造成的模型复杂度过高.Mallows[3]基于预测精度的角度下提出了CP准则，选择使CP的值达到最小的模型作为最优模型.Hoerl和Kennard[4]提出了岭回归(ridge regression)的变量选择方法.除了上述方法，常用的传统变量选择方法还有逐步回归、最优子集回归、岭回归等.许多研究表明，传统的变量选择方法总是由于某些客观条件的限制，诸如协变量的维数很大等而表现的不尽如人意.近年来基于惩罚函数类型方法的出现在很大程度上使得变量选择方法有较大的发展，开创了变量选择方法的新景象.Tibshirani[5]提出了LASSO的变量选择方法.Fan 和Li[6]提出了SCAD的变量选择方法.Fran 和 Friedman[7]提出了桥回归(bridge regression)的变量选择方法.Zhang[8]发展了MCP的变量选择方法.Yohai[9]研究了稳健的FPE准则的变量选择.樊亚莉等[10]作出了纵向数据的稳健变量选择方法.Welsh[11]开创了基于bootstrap分层的稳健变量选择.Sophie 等[12]提出了结合惩罚项的稳健变量选择.

经验似然是构造置信区间和检验非参数的一门统计技术，类似于bootstrap的抽样特性，这一方法与其它的统计方法相比有很多突出的优点.最早，Owen[13]在完全样本下提出了一种进行非参数类型的统计推断方法，并且将经验似然方法的应用推广到线性回归模型的统计推断中.Kolaczyk[14]把经验似然方法应用到了广义的线性模型.Chen[15-16]研究了非参数的回归的经验似然统计推断.近些年来，关于经验似然的研究也在不断的发展中.Qin 和Lawless[17]研究了约束情况下参数的估计方程在经验似然中的统计推断.还有在复杂数据下所用到的一些经验似然方法，如Wang 等[18]在删失数据的一类生存函数中用到了经验似然；Rao等[19]研究了带缺失数据的线性模型的经验似然统计推断.

本文对普通的惩罚经验似然方法提出了改进，详细讨论基于经验似然方法的稳健变量选择问题.具体来说，我们把普通经验似然约束中的估计方程稳健化，提出了稳健经验似然估计，再把惩罚经验似然方法和稳健估计方程结合起来，提出了一种惩罚稳健经验似然的压缩估计方法，从而达到稳健估计和变量选择同时进行.通过数值模拟分析，该新方法在变量的准确度和非零参数估计的均方误差上优于普通的惩罚经验似然估计.因此，本文的方法在变量选择等数据分析中具有一定的优势.

以下的内容安排如下.第2节介绍本文考虑的模型，以及基于惩罚稳健经验似然的压缩估计方法，第3节介绍本文的迭代算法和调节参数的选取方法，第4节进行数值模拟，第5节是实证分析，第6节为本文的总结.

2 模型和方法

2.1 线性回归模型

考虑简单的线性模型：

Y=XTβ+ε,

(2.1)

其中Xi=(Xi1,Xi2,…,Xip)T为解释变量，i=1,2,…,n，Y=(Y1,Y2,…,Yn)T为响应变量，β=(β1,β2,…,βp)T为回归系数，ε=(ε1,ε2,…,εn)T为随机误差，ε1,ε2,…,εn独立同分布，且E(εi)=0，Var(εi)=σ2，i=1,2,…,n.待估计的参数为β，σ2.

2.2 普通的惩罚经验似然估计

普通的最小二乘估计是基于以下估计方程得来的：

(2.2)

根据Owen[13，20]，模型(2.1)的普通经验似然(EL)函数可表示为

满足上式的β与pi，可以通过拉格朗日乘数法求解.令

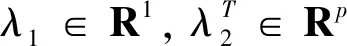
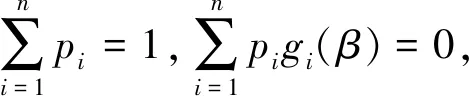
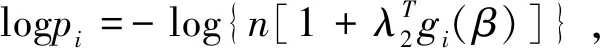
(2.3)

普通的经验似然函数为

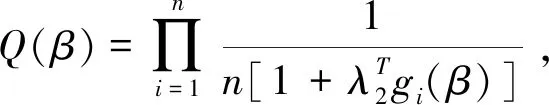
对数经验似然函数为

(2.4)

为了达到变量选择的目的，我们在对数经验似然函数的基础上加惩罚项，得到如下的惩罚经验似然函数

(2.5)

惩罚函数的选取有多种形式，如文献[5]提出的LASSO，文献[8]提出的MCP.本文选取文献[6]提出的SCAD.SCAD惩罚函数具有无偏性、稀疏性、连续性.无偏性保证了系数较大的变量其估计系数是渐近无偏的，这样避免了不必要的模型偏差.稀疏性保证了将不太重要的系数压缩为零，从而起到选择变量、降低模型复杂度的效果.连续性是减少了模型预测时的不稳定性，保证了数据本身的连续性.因此本文选取SCAD惩罚函数.

SCAD惩罚函数具有如下形式：

其中λ>0，a>2.根据文献[6]，其一阶导数为

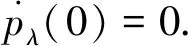
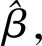
2.3 稳健的惩罚经验似然估计

(2.2)式所定义的估计方法对数据中的异常值是异常敏感的，因此，基于(2.2)式的普通惩罚经验似然估计也会由于异常值的存在而有较大偏差.为了降低异常值的影响，把(2.2)式稳健化，采用有界的得分函数来限制估计方程中异常值的影响.记ψc(x)为对应于Huber函数的得分函数.函数ψc(x)的定义为

ψc(x)=min{c,max{-c,x}},

其中调节参数c用来调节估计的效率和稳健性.对于学生化残差Xi,c的取值一般介于1到2之间.

与文献[21]类似，我们采用如下的权重函数来限制杠杆点的影响：

记

其中σr为σ的绝对离差估计.

稳健经验似然函数可表示为：

Qr(β)的最大值点就是β的稳健经验似然估计.

加上惩罚函数的稳健经验似然函数为

(2.6)

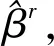
3 算法

3.1 基于SCAD的稳健惩罚经验似然估计的牛顿迭代算法

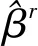
由于SCAD惩罚函数是非凸且不可导，直接最小化目标函数并不容易.利用局部二次逼近方法，对SCAD惩罚函数在初始值β0展开，有

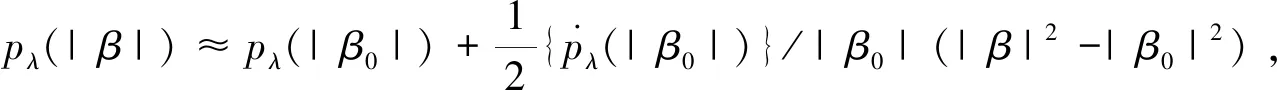
记

我们使用修改的牛顿迭代算法来执行惩罚经验似然函数的优化.具体而言，对于k=0,1,2,…，我们生成迭代序列

其中

重复上述迭代过程，当|β(k+1)-β(k)|<ξ时就停止迭代.这里我们指定ξ=10-6.

3.2 调节参数的选取

为了选择合适的调节参数，我们对普通的惩罚经验似然估计和稳健的惩罚经验似然估计都运用BIC准则来选取调节参数.为了简单起见，在模拟时令所有的λ相等，即假设λ(j)=λ,j=1,2,…,p.我们在区间Ω=(0,λmax)中选择最佳的λ.根据文献[23]，

BICλ=log(RSS)+dfλlog(n)/n,

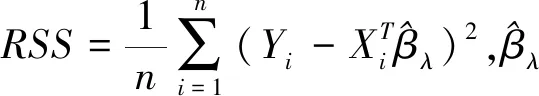
4 数值模拟

为了比较稳健的惩罚经验似然方法及压缩估计在有限样本下的性质,我们通过数据模拟试验来进行说明.

4.1 数据的产生

我们从模型(2.1)产生模拟数据，这里参数设定为β=(3,3,0,0,2.5,0,0,0)T，p=8，Xi=(Xi1,Xi2,…,Xip)T的每个分量服从N(0,1)，样本大小n=50，对每组数据重复模拟N=200次.对于误差项εi的分布，我们考虑三种情况：

(1)εi服从标准正态分布N(0,1)，且数据无污染；

(2)εi服从标准正态分布N(0,1)，但数据被污染；

(3)εi服从厚尾的t(2)分布.

4.2 数据的3种污染方式

污染1：仅对解释变量X的污染, 随机污染3%的Xi，并将其替换为Xi-1.2；

污染2：仅对响应变量Y的污染, 随机污染3%的Yi，并将其替换为Yi-1.2；

污染3：解释变量X和响应变量Y同时污染, 随机污染3%的Xi，并将其替换为Xi-1.2，随机污染3%的Yi，并将其替换为Yi-1.2.

数值模拟的结果如下面各表所示.

表1 正态分布时数据没有污染时的模拟结果

由表1可知，在模拟数据无污染的情况下，本文所提出的稳健惩罚经验似然方法及压缩估计在非零参数估计的变量选择准确度上相同于最小二乘估计和普通的惩罚经验似然估计，但在参数为零的估计上明显优于最小二乘估计，在非零参数的均方误差下优于普通的惩罚经验似然估计.

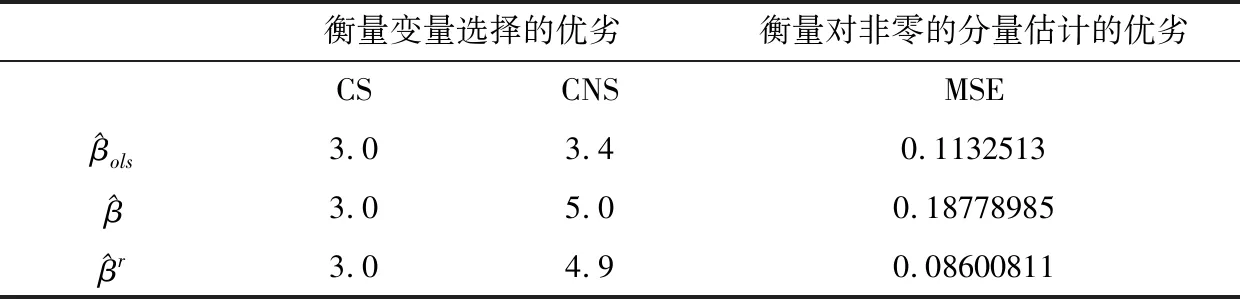
表2 正态分布时数据在污染1下的模拟结果

表3 正态分布时数据在污染2下的模拟结果

由表2和表3可知，无论是在解释变量污染，还是在响应变量污染的情况下，本文所提出的方法在非零参数估计的变量选择准确度上相同于最小二乘估计和普通的惩罚经验似然估计，但在参数为零的估计上明显优于最小二乘估计，在非零参数的均方误差下优于普通的惩罚经验似然估计.

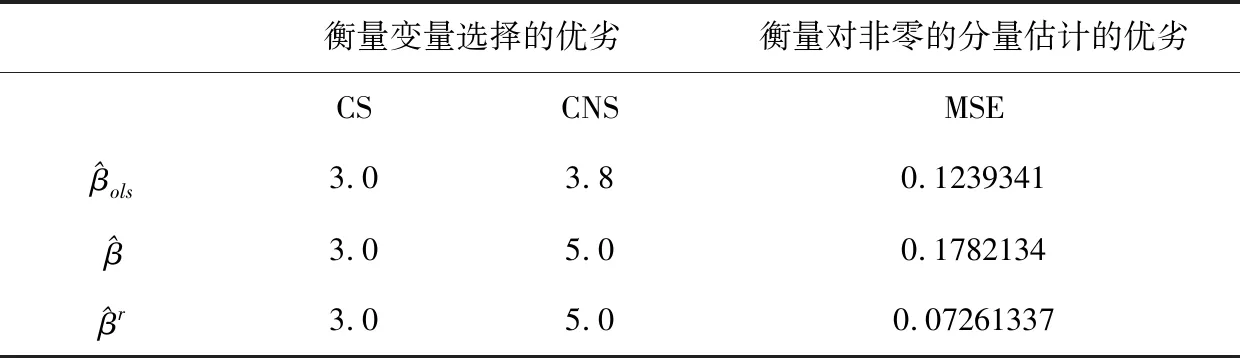
表4 正态分布时数据在污染3下的模拟结果

由表4可知，即使在解释变量和相应变量都污染的情况下，本文所提出的方法在非零参数估计的变量选择准确度上相同于最小二乘估计和普通的惩罚经验似然估计，但在参数为零的估计上明显优于最小二乘估计，在非零参数的均方误差下优于普通的惩罚经验似然估计.

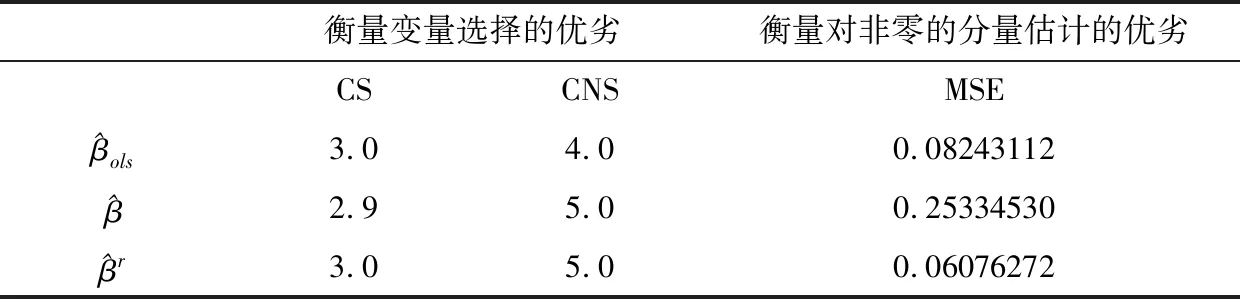
表5 t(2)分布时数据的模拟结果

由表5可知，不管是模拟数据在正态分布的情况下，还是在自由度为2的厚尾t分布情况下，本文所提出的方法在非零参数估计的变量选择准确度上仍然相同于最小二乘估计和普通的惩罚经验似然估计，但在参数为零的估计上还是明显优于最小二乘估计，在非零参数的均方误差下优于普通的惩罚经验似然估计.

在模拟研究中的变量选择效果上，本文提出的方法相较于普通的惩罚经验似然估计的优势似乎不太明显，这可能和参数β=(3,3,0,0,2.5,0,0,0)T的设置有关，因为我们取了非零的值比较大，信号比较明显.

5 实证分析

在本小节中，我们将稳健的惩罚经验似然方法及压缩估计应用到一组实际数据： Boston房屋数据.Harrison等[24]用这组数据在各种方法下研究了人们对于干净空气的需求，这组数据来源于网址:http://t.cn/RfHTAgY.该数据的每个类的观察值是均等的，共有506个观察值，13个解释变量和1个响应变量，其中解释变量包括：城镇人犯罪率(CRIM)，住宅用地超过25000 sq.ft.的比例(ZN)，城镇非零售商用土地的比例(INDUS)，查理斯河空变量(如果边界是河流取1，否则取0)(CHAS)，一氧化氮浓度(NOX)，住宅平均房间数(RM)，1940年之前建成的自用房屋比例(AGE)，到波士顿五个中心区域的加权距离(DIS)，辐射性公路的接近指数(RAD)，每10000美元的全值财产税率(TAX)，城镇师生比例(PTRATIO),1000(BK-0.63)^2(其中BK指代城镇中黑人的比例)(B),人口中地位地下者的比例(LSTAT).响应变量：自住房的平均房价，以千美元计(MEDV).考虑到实际的数据各项指标单位不同的数值差异较大，因此先将各项指标标准化，使其均值为0，方差为1.

为了比较，我们将这组数据做了交叉验证来比较稳健的方法和普通的非稳健方法的表现.每次剔除1个观察值，然后用剩下的505个观察值的回归系数，并用模型在交叉验证过程中的均方误差(MSEcv)来衡量各种方法的优劣：

表6 稳健与非稳健方法对自住房平均房价的MSEcv和Varcv 的估计比较

MSEcv值越小，表示该变量选择的效果越好.在表6中可以看出最小二乘估计的MSEcv最小，但最小二乘估计不做参数压缩和变量选择，它把所有的参数值估计为非零，而稳健的方法和非稳健的方法都做变量选择，并且做压缩估计.综合来看，本文提出的稳健惩罚方法最好.

6 结论

本文提出稳健的惩罚经验似然方法及压缩估计，给出了相应的算法，并作了大量的模拟研究.根据数值模拟研究表明，在数据无污染时，我们提出的方法在衡量变量选择的优劣中具有较高的准确度，在非零分量估计的均方误差下相对较小；在数据污染的情况下，本文的方法在选择准确性和估计的均方误差方面的优势尤为显著.所以，本文的稳健压缩估计方法在变量选择中具有一定可行性的优势.

本论文稳健的惩罚经验似然方法及压缩估计可以推广到纵向数据，也可以结合其他的惩罚函数，如LASSO[5]的变量选择方法，MCP[8]的变量选择方法等与SCAD的变量选择方法来做比较.当然，证明本文方法的理论性质,如变量选择的相合性，以及压缩估计的渐近正态性，还需要做进一步研究.