基于时间序列模型的上海市机构养老床位供给预测

(1.上海理工大学管理学院,上海,200093；2.上海市民政局信息研究中心,上海,200125)

1 引言

在中国“十一五规划”过程中上海市率先提出“9073”的养老模式.这一模式受到了许多专家的认可，即90%的老年人由家庭自我照顾、7%享受社区居家养老服务、3%享受机构养老服务.西方发达国家平均有5%-15%的老年人采用机构养老，其中北欧大约为5%-12%，英国大约为10%，美国大约为20%.然而中国只有3%，甚至不足3%.同时中国社会养老服务的需求越来越大，现有的养老设施总量很难满足日益增长的养老需求，实现社会养老资源的合理分配是亟待解决的问题之一[1-4].

陶卓霖等预测了在自然增长状态下2020年北京市老龄人口的分布以及利用粒子群方法对养老设施的分布进行优化[5]；胡苏云等针对上海市养老服务业提出了整体的规划与建议[6]；李小云等基于养老需求为导向，预测2020年和2030年南昌市的老人人口以及分布，以及对养老设施的建议等等[8-9].以上各类研究在养老资源分配的研究方面较少.本文针对上海市的养老事业发展现状，利用时间序列模型预测2019年和2020年上海市及各个市区的老人数，并进一步预测所需的养老床位，寻求更合适的方案实现养老资源的有效合理分配.

2 相关理论

2.1 指数平滑法

指数平滑法通过计算指数平滑值，结合一定的时间序列预测模型进行预测.依据平滑次数不同，可分为一次指数平滑法、二次指数平滑法、三次指数平滑法等[10].

(1)布朗单一参数线性指数平滑模型

布朗单一参数线性指数平滑模型属于二次指数平滑法，利用平滑值对时间序列的线性趋势进行修正，进而利用线性平滑模型进行预测[10].该模型适用于线性趋势的时间序列预测.布朗单一参数线性指数平滑模型的数学表达式为：

(1)

(2)

(3)

(4)

ft+m=αt+btm，

(5)

(2)霍尔特双参数线性指数平滑模型

霍尔特双参数线性指数平滑模型属于二次指数平滑法，该模型适合分析有增长或降低趋势的、没有季节性的相加的时间序列模型，并进行短期预测[10].霍尔特指数平滑法分别对时间数列的两种因素进行平滑，公式如下：

st=αyt+(1-α)(st-1+bt-1)，

(6)

bt=β(st-st-1)+(1-β)bt-1，

(7)

Ft+T=st+btT，

(8)

其中，α、β为平滑参数；yt为实际观察值；T为预测时期数；bt为趋势值.st为平滑值.

2.2 ARIMA模型

ARIMA模型为自回归积分滑动平均模型，先将时间序列转化为平稳的时间序列，然后将因变量对它的滞后值以及随机误差项的现值和滞后值进行回归分析.根据原序列是否平稳以及回归中所含部分的不同，包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程.

ARIMA模型的数学形式为：

Y(t)=u+Ø1y(t-1)+Ø2y(t-2)+…+Øpy(t-p)+ε(t)+φ1ε(t-1)+…+φqε(t-q)，

(9)

其中：u表示常数项，Ø1，Ø2,…，Øp为自回归系数，满足平稳性条件；φ1，φ2，…，φq为滑动平均系数；ε(t)为白噪声序列.上式称为p阶自回归q阶滑动平均模型，记为ARIMA(p,d,q)，其中d为使时间序列成为平稳时所做的差分次数[10].

2.3 评估方法

(1)R方：用来估计由模型解释的变异在总变异中的比例.当序列很平稳时，此度量较为有效.R方可以是负无穷大到1范围中的负值.负值表示考虑中的模型比基线模型差.正值表示考虑中的模型比基线模型好.

(2)RMSE：为均方根误差，用来度量原始因变量与预测值之间的误差，用和因变量序列相同的单位表示.

(3)MAPE：平均绝对误差百分比，度量因变量序列与其模型预测水平的相差程度.它与使用的单位无关，因此可用于比较具有不同单位的序列.

3 数据与模型

3.1 数据来源

本文研究的数据来源为上海市民政局民政业务数据海，经过整理得到的数据主要为：2004-2018年的上海市与各区的年老人总数、机构养老的年老人总数、上海市可以为每个区提供的年机构养老床位总数3种时序数据.

3.2 模型构建

3.2.1 模型构建步骤

Step 1：数据准备.由于上海市民政局业务数据海的数据已是相对标准的数据，且每组数据内部的差异并不是非常显著，因此原始数据可不经过任何归一化、标准化操作即可代入模型.

Step 2：模型及其参数估计.将当前时刻的原始值yt作为目标值，t-i时刻的原始值yt-i(i=1, 2, …)作为自变量，分别代入布朗单一参数线性指数平滑模型、霍尔特双参数线性指数平滑模型、ARIMA模型中进行拟合，其中指数平滑法及ARIMA模型中的参数或系数均使用最小二乘法进行估计.

Step 3：模型选择.通过比较R方、均方根误差拟合效果评价指标，选择拟合度最好的模型进行下一步分析.

Step 4：预测.利用Step3中所得模型对上海市及各区的年老人总数、养老机构老人总数、机构年总床位数进行预测.

3.2.2 实证分析

以预测2019年和2020年徐汇区老人数量为例进行算例分析.

首先，按如下方法建立布朗单一参数线性指数平滑模型.

(10)

当m=1时，将公式(1)、(2)、(3)、(4)代入(10)中，得到最终的参数优化函数：

(11)

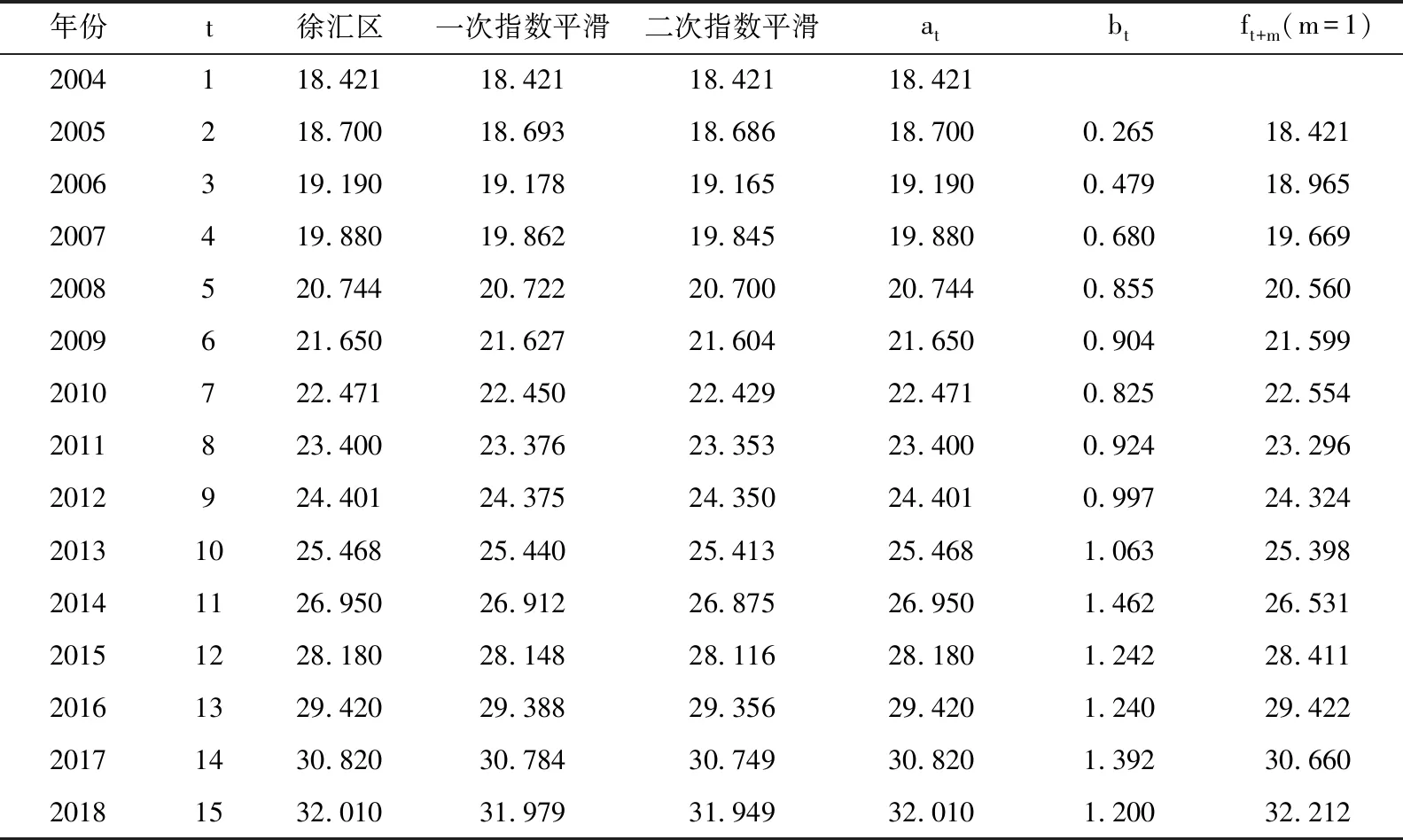
表1 布朗单一参数线性指数平滑模型

然后，建立霍尔特双参数线性指数平滑模型。

当T=1时，最终优化参数函数可表示为：

(12)

对式(12)应用最小二乘法，求得最优参数α=0.9,β=1.再由式(6)、(7)、(8)得到霍尔特拟合值，如下表2所示.

表2 霍尔特双参数线性指数平滑模型

在代入ARIMA之前，将徐汇区老人数据进行2次差分运算，得到平稳数据.对平稳后的数据，使用SPSS软件观察其所对应的自相关和偏相关图，得到ARIMA中的模型参数为p=0,d=2,q=0.因此可建立如下的ARIMA(0,2,0)模型：

Y(t)=u+2y(t-1)-y(t-2).

通过最小化预测值与实际值的差异，即min(u+2y(t-1)-y(t-2)-yt)2，获得二次差分下ARIMA的常数项u的值为0.07.

因此，ARIMA(0,2,0)的最终预测公式为：Y(t)=0.07+2y(t-1)-y(t-2).计算所得拟合值，如表3所示.

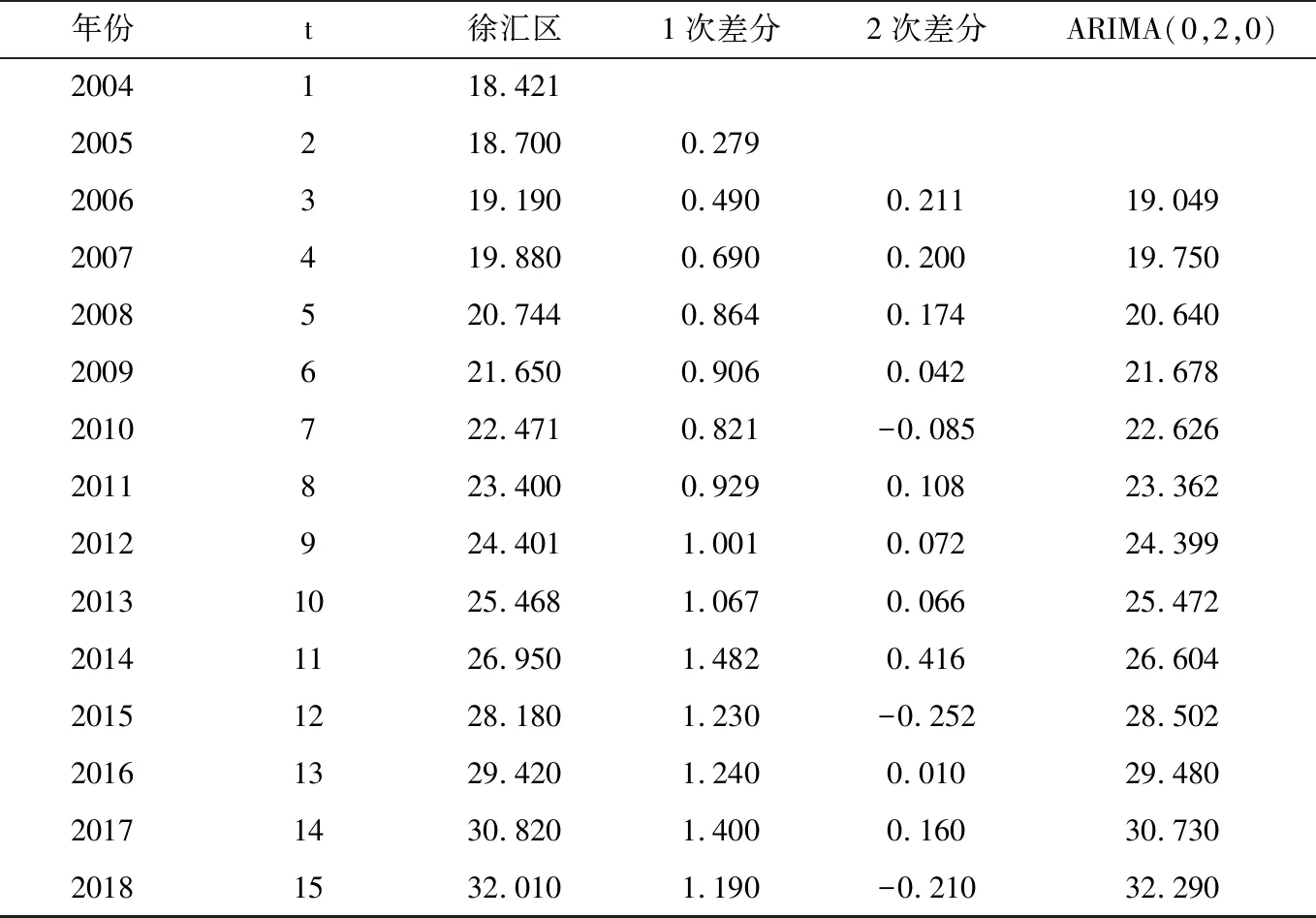
表3 ARIMA(0,2,0)模型

对表1，表2，表3中的拟合预测结果，运用R方和RMSE公式计算实际值与拟合值的差异，运算结果分别为0.998与0.175、0.998与0.185、0.998与0.18，因此在徐汇区老人数据下，选择布朗单一参数线性指数平滑模型.

3.3 结果分析

(1)上海市及其市区的老人数预测模型

以2004-2018年上海市及各个市区老年人数作为样本，应用SPSS软件中的专家建模时序方法，专家建模器会从上述3种方法中以R方、最大绝对误差百分比、均方根误差、平均误差百分比等作为评估标准自动选择每个序列的最佳拟合模型.上海市及各区老人总数适用的最优模型及其对应的评估效果值如下表4所示.

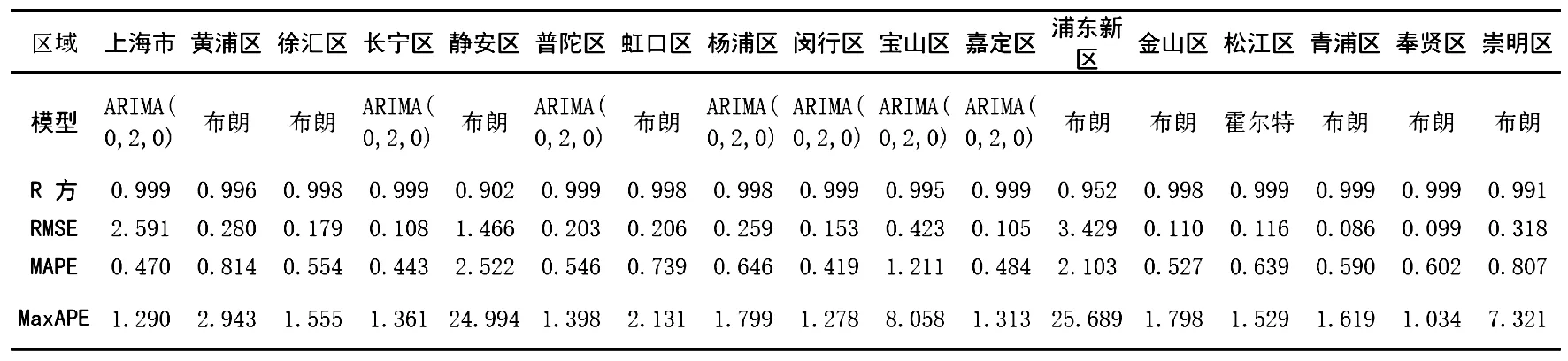
表4 上海市及各个市区的老人数预测模型

在表4中，上海市及其各个市区所用的模型并不相同，其中上海市采用ARIMA(0,2,0)模型，表示ARIMA模型中自回归项为0，差分次数为2，移动平均项为0.上海市长宁区、普陀区、杨浦区、闵行区、宝山区、嘉定区采用ARIMA(0,2,0)模型，松江区采用二次指数平滑中的霍尔特模型，其他区则采用二次指数平滑中的布朗模型.同时，各组数据在相应最优模型下的R方值均高于95%，其他三种评估指标也很小，表明模型具有较好的拟合效果.

(2)机构养老的老人数预测模型

以2004-2018年上海市各个区机构养老的老年人数作为样本，应用SPSS进行模型选择，在这组数据下各个区的机构养老模型选择结果及其效果评估如下表5所示.

表5 上海市各个市区的机构养老老人数预测模型

其中，上海市黄浦区、徐汇区、长宁区、普陀区、杨浦区、嘉定区、崇明区采用ARIMA(0,1,0)模型，表示ARIMA模型中自回归项为0，差分次数为1，移动平均项为0；其余各区则采用二次指数平滑中的霍尔特模型.同时，各组数据在相应最优模型下的R方值均高于90%，其他三种评估指标也很小，模型具有较好的拟合效果.

(3)机构养老的床位供给预测模型

以2004-2018年上海市各个区机构年供给的床位总数作为样本，应用SPSS进行模型选择，在这组数据下各个区的机构床位供给预测模型选择结果及其效果评估如下表6所示.

表6 上海市各个市区的机构养老床位供给模型

其中，上海市杨浦区、崇明区采用ARIMA(0,2,0)模型，表示ARIMA模型中自回归项为0，差分次数为2，移动平均项为0；其余各区则采用二次指数平滑中的布朗模型.同时，各组数据在相应最优模型下的R方值均高于93%，其他三种评估指标相对较小，模型具有较好的拟合效果.

4 上海市机构养老床位供给预测

首先预测上海市及其各个市区的老人数，然后依据老人数以及入住机构老人数趋势，预测入住养老机构的老人数，最后对2019年和2020年上海市各个市区的床位供给分配情况进行预测.

4.1 上海市及各区的老人数预测

上海市及各个区选择上述拟合度最佳的时间序列模型，预测2019年上海市老人数达到526.1867万人，其中上限值为531.8331，下限值为520.5403.2020年预测老人数达到550.3301万人，其中上限值为562.9558，下限值为537.7044.2018年年末老年人数为503.28万人，2019年相对于2018年增长了4.55%，2020年相对于2019年增长了4.59%.可见老龄化越来越严重，老年人数的增长比率也在慢幅度上升.

2019年上海市各个区的老人数量预测结果如表7所示.由表7可知，浦东新区的2019年老人数预测可能会突破100万人，上限为107.278万人.相对于2018年的增长比率除了静安区，均在3%以上.其中宝山区的增长率达到了7.26%，其次为嘉定区，为5.58%，最低则为静安区，不足3%.

表7 2019年上海市各个市区的老人数预测(单位：万人)

2020年上海市各个区的老人数量预测结果如表8所示.由表8可知，浦东新区的2019年老人数预测已超过100万人，上限为120.7957万人.相对于2019年的增长比率仍是除了静安区，均在3%以上.其中宝山区的增长率达到了7.41%，其次则为嘉定区，为5.55%，最低则为静安区，不足3%.相对于2019年，老人人数仍在上升，但增长比率却有增有减.长宁区、普陀区、杨浦区、虹口区、宝山区、松江区的增长率增加，其余市区增长率降低，但增减的浮动不大，均小于1%.

表8 2020上海市各个市区的老人数预测(单位：万人)

4.2 机构养老的老人数预测

结合历年老人总数与机构养老的老人数的比例趋势以及机构养老老人数随着时间的变化趋势，对2019年和2020年即将可能入住养老机构的老人数量进行预测.2019年、2010年上海市各个区的入住养老机构老人数量预测结果分别如表9、表10所示.2019年以及2020年全市入住养老机构老人数最多的区为浦东新区，青浦区为人数最少区.2020年浦东新区的入住养老机构的老人数会突破2万人.而青浦区则仍不足2000，这与各个区的老人数有较大关联.入住机构养老的趋势仍在增长，故进一步预测床位供给.

表9 2019年上海市各个市区的机构养老老人数预测(单位：人)

表10 2020年上海市各个市区的机构养老老人数预测(单位：人)

4.3 机构养老的床位供给预测

2019年、2010年上海市各个区的机构养老床位供给数量结果分别如表11、表12所示，其中入住率为预测得到的入住养老机构的老人数和床位供给数之比.各个区的入住率约在60%到90%之间，其中只有青浦区会低于60%，但相差不超过2%，普陀区的入住率超过了90%.可在以后的研究中考虑市区之间的床位供给协调.既满足了老人床位的需求，也实现的养老床位充分使用.

表11 2019年上海市各个市区的机构养老床位供给预测(单位：个)

表12 2020年上海市各个市区的机构养老床位供给预测(单位：个)

5 结论

本文基于预测2019年、2020年上海市及其各个市区的老年人口数量，以及上海市“9073”的养老模式，为3%的老年人提供机构养老的政策目标，选择拟合程度最佳的时间序列模型，得出上海市各个区在2019年和2020年应提供的机构养老床位数量.养老床位数量与预测得出的入住养老机构的老人数的比率即入住率大都在60%到90%之间，青浦区低一些，普陀区则高一些.研究结果对上海市在进行床位供给的政策制定有一定的参考价值，对其他地区也有一定的借鉴意义.

本文的研究也存在一定的局限性.由于对养老床位的供给预测只考虑了老年人口增长的因素，并未考虑经济和文化等方面因素，为了寻求更合理的预测方案，需在这些方面进行相应的考虑.此外，存在有的市区入住率过高，而有的区入住率则比较低的现状，后续可考虑在市区之间床位的分配协调问题进行研究.

本文由上海市民政局科研课题项目支持，部分数据由上海市民政业务数据海提供，特致谢.