一类带记忆项拟线性发展方程的适定性
(长沙理工大学数学与统计学院,长沙,410001)
1 引言
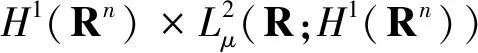
(1.1)
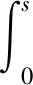
(1.2)
另外, 对于记忆核和非线性项有如下假设:
(H1)对记忆项核的假设:
μ∈C1(R+)∩L1(R+),μ(s)>0,∀s∈R+
(1.3)
且存在δ>0, 使得
μ′(s)+δμ(s)0,∀s∈R+.
(1.4)
记
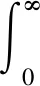
(H2) 对非线性项的假设: 假设f∈C1,f(0)=0, 且满足如下增长条件
α1|s|p-β1|s|2≤f(s)s≤α2|s|p+β2|s|2,∀s∈R,p≥2
(1.5)
和耗散条件
f′(s)≥-l
(1.6)
且β1<λ, 其中αi,βi(i=1,2)和l都是正数.
方程(1.1)作为数学物理模型,通常应用于流体力学、固体力学和热传导理论等领域[1,2],其主要考虑了两个方面的影响,其一是粘性,其二是u的过去历史影响(例如聚合物、高粘度液体等[3]); 当考虑这两个影响因素时,就构成了揭示扩散的全部过程的能量方程,即上述带记忆项的发展方程(1.1),也就是我们常说的非经典扩散方程.
当方程(1.1)不带记忆项的时候,其无界域上解的存在性及其渐近行为已经被很多人研究过[4-6].据我们所知,对方程(1.1)这种带有记忆项的问题的相关研究还很少,本文将应用分析技巧和Galerkin方法解决该问题.

由于在无界域上、非线性项满足任意阶多项式增长以及记忆项这三个因素的影响,本论文存在两个主要的困难:一方面是Sobolev紧嵌入不再适用,另一方面是积空间的Galerkin方法不能用来逼近.本文应用Xie[4]与 Ma[5]的基本思想和方法,结合分析技巧来克服上述困难, 由此证得解的存在性,进而获得解的唯一性和解对初值的连续依赖性.
2 预备知识
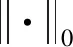
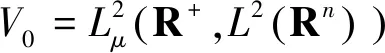
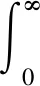
那么, 方程的相空间为
M1=H1(Rn)×V1,
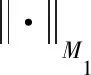
u的时滞变量uτ(-s)满足以下条件:存在R>0和ρ≤δ(δ来自于(1.4), 使得
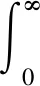
(2.1)
3 解的存在性
定义3.1设f(u)满足(1.5)-(1.6),z0=(u0,η0)∈M1.z=(u,ηt)称为方程(1.1)的整体弱解,如果对∀T∈R,z满足方程(1.1)并且
u∈C([0,T];L2(Rn))∩L2([0,T];H1(Rn)),ut∈L2([0,T];L2(Rn)),
另外,对任意ω(x)∈H1(Rn),φ(x,t)∈V1有
对于t∈R几乎处处成立.
对于解的存在性,通过下面的一些引理,可得到定理3.5.
首先,对任意的正整数n,我们给定一个球
Bn={x∈Rn:|x| (3.1) 因为Bn是有界域, 所以利用标准的Faedo-Galerkin方法可以获得如下初边值问题解的存在性 (3.2) 其初始条件为: (3.3) 边界条件为: (3.4) 其中χn(x)为一个光滑函数,满足 引理3.2假设T>0,f∈C1(R)且满足条件(1.5)-(1.6),核函数μ满足(H1),而g∈H-1(Rn),则对于任意的t∈[0,T],有如下估计: 其中C1仅依赖于T,但不依赖于n. 证明对(3.2)中的第一个方程乘以un,在Rn上积分并利用条件(1.5),可得 (3.5) (3.6) 于是(3.5)可改写为 (3.7) 由Gronwall引理, 对一切的t∈[0,T]有 (3.8) 并且(3.7)两边对t在[0,T]上积分, 有 (3.9) 取 结合(3.8)-(3.9)知引理结论成立.证毕. 其中C2仅依赖于T,但不依赖于n. (3.10) 由Gronwall引理及引理3.2,对一切t∈[0,T]有 (3.11) 再对(3.11)在0到t上进行积分,可得 (3.12) 引理3.4假设引理3.2的假设条件成立,则存在不依赖n的正常数C3,C4,使得对所有的t∈[0,T], α3|un|p-β3≤F(un)≤α4|un|p+β4, (3.13) 其中αi,βi(i=3,4)均为正数. 对(3.2)中的第一个方程乘以unt,再在Rn上积分,得到 (3.14) 由Hölder不等式和Young不等式,我们有 (3.15) 这里m0来自假设(H1),且 (3.16) 令 (3.17) 则有 (3.18) 仿照文献[4]中引理3.4的证明可得,存在与n无关的正常数C3,使得对一切的t∈(0,T]有 进一步,由(3.13)式, 可得 (3.19) 对(3.18)式关于t在(0,T]上进行积分,并结合引理3.2和引理3.4,即知存在与n无关的正常数C4,使对一切t∈(0,T]有 证毕. 由以上的论述,可以得到如下关于方程(1.1)解的存在性定理. 定理3.5假设条件(H1)-(H2)成立,则对任意的T>0和z0=(u0,η0)∈M1,方程(1.1)存在弱解z=(u,ηt),且满足u∈L∞(0,T;H1(Rn)),ηt∈L2(0,T;V1). un在L∞(0,T;H1(Rn))∩L2(0,T;H1(Rn)) 一致有界, unt在L2(0,T;H1(Rn)) 中一致有界, un⇀u在L2(0,T;H1(Rn))中弱收敛, unt⇀ut在L2(0,T;H1(Rn))中弱收敛, (3.20) 取ρ0=CC3+CC1T,由引理3.4可得 (3.21) 同理,当un∉Bn时,取un=0,将un延拓到整个Rn上, 则有 f(un)→χ在Lq((0,T]×Rn)弱收敛. f(un(x,t))→f(u(x,t))于[0,T]×Rn上几乎处处收敛. (3.22) 所以在Lq([0,T]×Rn)⊂H-1([0,T]×Rn)中f(un)⇀f(u),且由弱极限的唯一性可知:χ=f(u). 另外,由于gn(x)∈H-1(Bn),对于一切的x∈Rn,有gn→g(n→∞), 从而g(x)∈L2(0,T;H-1(Rn)). 证毕. 定理4.1假设条件(H1)-(H2)成立,则对任意T>0和z0=(u0,η0)∈M1,方程(1.1)在M1中有唯一弱解z=(u,ηt), 且解z(t)=(u(t),ηt)连续依赖于初值z0=(u0,η0). (4.1) 对方程(4.1)两端用ω作用,可得 (4.2) 对(4.2)式的右端项,我们有 (4.3) 其中CR与t无关,故由Gronwall引理得到 这就证明了方程(1.1)解的唯一性和对初值得连续依赖性.证毕.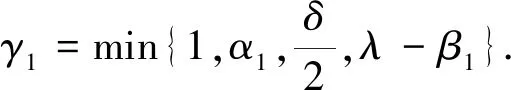

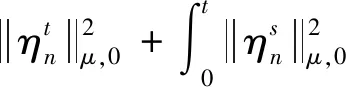

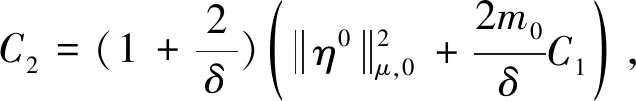
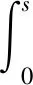

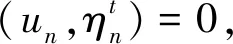


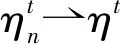
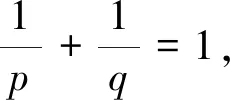
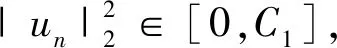
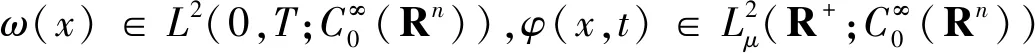
4 解的唯一性和对初值的连续依赖性




