关于线性丢番图方程的Frobenius问题
(中山开放大学,中山,528403)
1 引言与主要结果
考虑k(≥2)个变元的线性丢番图方程:
a1x1+…+akxk=b,
(1.1)
这里a1,…,ak,b皆为正整数,满足条件
(a1,…,ak)=1.
(1.2)
可以证明[1]:当整数
b≥(ak-1)(a1+…+ak-1)
(1.3)
时,方程(1.1)总存在非负整数解(x1,…,xk).因而,存在一个最小的整数G(a1,…,ak),使得当整数b≥G(a1,…,ak)时,方程(1.1)总存在非负整数解;而当b=G(a1,…,ak)-1时,方程(1.1)不存在非负整数解.
Frobenius问题是找到G(a1,…,ak)的具体表示形式.熟知当k=2时,有[1,2]
G(a1,a2)=(a1-1)(a2-1).
(1.4)
而对于k>2,尚未见到类似的表示形式.M. B. Nathanson称这是一个困难的开问题[1](a difficult open problem).
本文的目的,是要借助于(1.4)式,对于k>2,给出G(a1,…,ak)的一种表示形式.
不失一般性,本文始终假设a1 (a1,…,ak)={b;b>a1为正整数且使得方程(1.1)没有非负整数解}, (1.5) 称之为相对于a1,…,ak的非负不可解集.显然,它是一个有限集合,而且成立 G(a1,…,ak)=max(a1,…,ak)+1. (1.6) 例1.1(3,7)={4,5,8,11},(3,7,11)={4,5,8}.G(3,7)=12,G(3,7,11)=9. 我们的主要结果是: 定理1.2设k(≥3)个正整数a1 (1.7) …… 本节,我们给出一个后面常常要用到的结论. 引理2.1给定整数a>b>0,(a,b)=1.如果整数i满足:0 0 (2.1) 使得 nb+i=ka. (2.2) 证明考虑模a的剩余类形成的加法群,有 ={[0],[1],…,[a-1]}, 这里[i]表示i所在的剩余类. 另一方面,由(a,b)=1,还有 ={[0],[b],…,[(a-1)b]}. 于是,[i]在中的加法逆元可记为[nb].由i≠0可知n≠0,故得0 nb+i≡0(moda), 从而存在k,使得(2.2)式成立.由(2.2)式左端大于0,可知k>0,再由 ka=nb+i 可得kb.故得(2.1)的后半部分. 这就完成了引理的证明. 借助这个基本引理,我们可以给出(1.4)式一个构造性的证明. 不妨假设a1 a1a2-a1-a2=a1(a1q+r)-a1-a1q-r=a1((a1-1)q+r-2)+a1-r. 将方程(1.1)改记为 a1x1+a2x2=b. (2.3) 如果整数b>a1a2-a1-a2,则可记 b=a1a2-a1-a2+a1t+i, (2.4) 当i=0时,必有t>0,因而得到:b=a1(t-1)+a2(a1-1).这表明x1=t-1,x2=a1-1便是方程(2.3)的非负整数解. 当0 nr+a1-i=ka1, (2.5) 其中 0 (2.6) 由(2.5),可得 a1-r+i=(2-k)a1+(n-1)r. 于是有 b=a1a2-a1-a2+a1t+i=a1((a1-1)q+r-2+t)+a1-r+i =a1((a1-1)q+r-2+t)+(2-k)a1+(n-1)r =a1((a1-n)q+r-k+t)+(n-1)a2. 由(2.6),可知:(a1-n)q+r-k+t>0,n-1≥0.这表明x1=(a1-n)q+r-k+t,x2=n-1便是方程(2.3)的非负整数解. 如果整数b=a1a2-a1-a2,则方程(2.3)没有非负整数解.如若不然,就有x1≥0,x2≥0,使得:a1x1+a2x2=a1a2-a1-a2.即 a1(x1+1)+a2(x2+1)=a1a2. 由(a1,a2)=1,从上式可得:a1|(x2+1),a2|(x1+1).并据此导出: a1a2=a1(x1+1)+a2(x2+1)≥a1a2+a2a1=2a1a2, 矛盾!因而得出: G(a1,a2)=a1a2-a1-a2+1=(a1-1)(a2-1). 这就是(1.4)式. 依据(1.6)式,解答Frobenius问题,须要了解非负不可解集(a1,…,ak)的主要性质.而且,例1.1暗示着重要的关系式:(a1,…,ak)⊆(a1,…,ak-1)!因此,本节先讨论(a1,a2)的若干性质. 性质3.1(1,a2)=Ø. 证明由(1.4)式,G(1,a2)=0.从而得证结论. 0(a1,a2)={x;x∈(a1,a2),x (3.1) 和 1(a1,a2)={x;x∈(a1,a2),x>a2}. (3.2) 由G(2,a2)=a2-1,易得 性质3.21(2,a2)=Ø. 根据上述两个性质,以下我们总设:2 a2=a1q+r,q≥1,0 (3.3) 由(a1,a2)=1,可知 (r,a1)=1. (3.4) 性质3.3x∈0(a1,a2),当且仅当x=a1t+i,1≤t≤q,其中,当1≤t 证明是显而易见的. 记M=a1a2-a1-a2,由(1.4)式知M∈1(a1,a2).进一步,还有 性质3.4x∈1(a1,a2),当且仅当 x=M-l2a2-l1a1, (3.5) 这里 0≤l2≤a1-3, (3.6) 以及 0≤l1≤(a1-2-l2)q+r-2-tr, (3.7) 如果0≤tr≤1+l2使得 tra1≤(2+l2)r<(tr+1)a1. (3.8) 进一步,表示式(3.5)是唯一的. 证明首先,如果(3.5)式成立,且l1≥0,l2≥0,则方程 a1x1+a2x2=x 没有非负整数解.如若不然,则有 a1(x1+l1)+a2(x2+l2)=M. 这与(1.4)式相矛盾! 进一步,为使x∈1(a1,a2),须x>a2,即 M-l2a2-l1a1>a2. (3.9) 此即a2(a1-2-l2)>a1(l1+1)>0,因而须a1-2-l2>0,故而得到(3.6)式. 现在来估计l1.当(3.8)式满足时,有 r<(tr+1)a1-(1+l2)r (3.10) 和 x=a1((a1-1-l2)q+r-2-tr-l1)+(tr+1)a1-(1+l2)r. (3.11) 如果 (a1-1-l2)q+r-2-tr-l1≥q, (3.12) 此即(3.7)式,将它和(3.10)一起代入(3.11)中,就得到(3.9)式.即有x∈1(a1,a2). 其次,如果x∈1(a1,a2),则有a2 x=a2+a1m+i,0 注意到i=a1-r时,x=a1(q+m+1)∉(a1,a2),故还有i≠a1-r. 现在应用引理2.1,有 nr+a1-i=ka1, (3.13) 其中0 记l2=a1-n-2,则(3.6)式成立.从(3.13)式,可得 r+i=a1(1-k)+(n+1)r. 因而有 a2+i=a1(q+1-k)+(a1-1-l2)r. 另一方面,有 M-l2a2=a1((a1-1-l2)q-1)+(a1-1-l2)r. 记m1=(a1-2-l2)q+k-2,则从上述两式可得 a2+a1m1+i=M-l2a2. 记l1=m1-m,则有x=a2+a1m+i=M-l2a2-l1a1.此即(3.5)式. 注意到l1<0时,M-l2a2-l1a1∉(a1,a2)(证明可见随后的性质3.6).故有l1≥0. 在(3.13)中,记k=r-t,并将a1-n=l2+2代入之,得 ta1<(t+1)a1-i=(2+l2)r<(t+1)a1. 将它与(3.8)式比较,可知t=tr,从而得到 0≤l1≤m1=(a1-2-l2)q+r-2-tr. 此即(3.7)式. 为证明表示式的唯一性,假设还有x=M-m2a2-m1a1,代入(3.5)中得到 (m2-l2)a2=(l1-m1)a1. 由(a1,a2)=1,可知a1|(m2-l2).再由|m2-l2|≤a1-3,可得m2-l2=0,代入上式,又可得m1-l1=0.因而唯一性得证. 至此便完成了性质3.4的证明. 由此性质,当a1=3时,l2=0,于是若x∈1(3,a2),则有 x=M-3l1=2a2-3(l1+1),0≤l1≤q-1. 注记3.5由(3.8)式可知,tr还是l2的函数.例如,取a1=5,a2=5q+4,即r=4.则有:l2=0时,tr=1;l2=1时,tr=2;l2=2时,tr=3. 因此,我们可以记tr=tr(l2).而且,由(3.8)式,有 这里[x]表示x的整数部分.由此,显然可见,当l2′≤l2″时,成立tr(l2′)≤tr(l2″). 性质3.6若l>0,0≤l2≤a1-3,0≤l1≤(a1-2-l2)q+r-2-tr,则有 M-l2a2+la1∉(a1,a2), (3.14) M+la2-l1a1∉(a1,a2). (3.15) 证明由 M-l2a2+la1=(a1-1-l2)a2+(l-1)a1 及a1-1-l2≥a1-1-a1+3=2,l-1≥0,可知(3.14)式成立. 又由 M+la2-l1a1=(a2-1-l1)a1+(l-1)a2 及a2-1-l1≥a1q+r-1-(a1-2)q-r+2+tr=2q+1+tr>0,l-1≥0,可知(3.15)式成立. 故性质3.6得证. 令 (3.16) 这里[x]表示x的整数部分. (3.17) 使得 M-l2a2-Nka1∈1(a1,a2) (3.18) 以及 k(M-l2a2-Nka1)=M-(k(l2+1)-1)a2-jka1∈1(a1,a2). (3.19) 证明对于整数k≥2,由a2>3,显然有k<(k-1)(a2-1),于是存在整数qk和rk,使得 (k-1)(a2-1)=kqk+rk,0 (3.20) 取jk=k-rk和Nk=qk+1,便得到(3.17)式. k((2+l2)q+1+tr)+jk 故有 (k-1)(a2-1)+jk≤ka2-k(2+l2)q-k(2+tr), 进而导出Nk≤(a1-2-l2)q+r-2-tr.由性质3.4,便得知(3.18)式成立. 由(3.17)式,可得 k(M-l2a2-Nka1)=M-kl2a2+(k-1)M-Nka1 =M-kl2a2+(k-1)(a2-1)a1-(k-1)a2 -(k-1)(a2-1)a1-jka1=M-(k(l2+1)-1)a2-jka1. 这是(3.19)式的前半部分. jk≤a2-1-k(2+l2)q-k(1+tr)=(a1-2-(k(l2+1)-1))q+r-2 -tr-(k-1)(q+1+tr)<(a1-2-(k(l2+1)-1))q+r-2-tr. 再由性质3.4,便得知(3.19)式成立. 故性质3.7得证. 事实上,(3.16)式定义的K(l2)还是a1,q和r的函数,故我们可记为: K(l2)=K(a1,q,r,l2). 易见,a1=4时,K(l2)≤1.一般地,我们有如下: 性质3.8设x=M-l2a2-l1a1∈1(a1,a2),则下列结论成立: 证明由(3.16)式知,K(l2)≤1等价于 (a1-2-l2)q+r-3-tr(l2)<(2+l2)q+2+tr(l2), 即 (a1-2(2+l2))q<5+2tr(l2)-r. (3.21) (3.22) 如果r=2s,则代入上式可得 由此导出tr(l2)=s-1,从而得知5+2tr(l2)-r=3.此时(3.21)式当q≥3时不成立. 如果r=2s+1,代入(3.22)式得到 由此导出s-1≤tr(l2)≤s,从而得知2≤5+2tr(l2)-r≤4.此时(3.21)式当q≥4时不成立. 这就得到结论(2). (3.23) 如果r=2s,则代入上式可得 由此导出s-2≤tr(l2)≤s-1,从而得知1≤5+2tr(l2)-r≤3.此时(3.21)式当q≥2时不成立. 如果r=2s+1,代入(3.23)式得到 由此导出s-1≤tr(l2)≤s,从而得知2≤5+2tr(l2)-r≤4.此时(3.21)式当q≥2时不成立. 这就得到结论(3). (3.24) 如果r=2s,则代入上式可得 据此导出tr(l2)≤s-1,从而得知5+2tr(l2)-r≤3.此时(3.21)式当q≥1时不成立. 如果r=2s+1,则由(3.24)式可得 据此导出tr(l2)≤s,从而得知5+2tr(l2)-r≤4.此时(3.21)式当q≥2时不成立. 这就得到结论(4). 至此性质3.8得证. 性质3.9若 0≤l1≤(a1-2-l2)q+r-2-tr(l2), 则有 k(M-l2a2-l1a1)=M-(kl2-(k-1)(a1-1))a2-(kl1+k-1)a1∈1(a1,a2). (3.25) 证明由 k(M-l2a2-l1a1)=M+(k-1)M-kl2a2-kl1a1 =M+(k-1)(a1a2-a2-a1)-kl2a2-kl1a1 =M-(kl2-(k-1)(a1-1))a2-(kl1+k-1)a1, 就得到(3.25)式的前半部分. =l2-(k-1)(a1-1-l2)≤l2-2(k-1) 其次,由0≤l1≤(a1-2-l2)q+r-2-tr(l2),显然有kl1+k-1>0.记 l2′=kl2-(k-1)(a1-1). 由注记3.5可得 于是有 kl1+k-1≤k(a1-2-l2)q+k(r-2-tr(l2))+k-1 =(a1-2-l2′)q+r-2-tr(l2′)-(tr(l2)-tr(l2′)+(k-1)(q+1+tr(l2)-r)). 从(3.10)式得到的 同时注意到(k-1)q-1>0,就得到 tr(l2)-tr(l2′)+(k-1)(q+1+tr(l2)) 因而导出 kl1+k-1<(a1-2-l2′)q+r-2-tr(l2′). 根据性质3.4,就得到(3.25)式的后半部分. 性质3.9得证. 对于每个x∈1(a1,a2),引进集合 1(x;a1,a2)={b;b∈1(a1,a2)且存在m>0,m1≥0,m2≥0使得b=mx+m1a1+m2a2} (4.1) 和 0(x;a1,a2)=1(a1,a2)1(x;a1,a2). (4.2) 如果a1=3,由性质3.4,当x∈1(3,a2)时,有 x=2a2-3(1+l1),0≤l1≤q-1. (4.3) 据此,当x=2a2-3q时,成立0(x;3,a2)=Ø,这是唯一的例外. 一般地,我们有 命题4.1如果a1>3,则对于每个x∈1(a1,a2),总有 0(x;a1,a2)≠Ø. (4.4) 证明依据性质3.4,当x∈1(a1,a2)时,有 x=M-l2a2-l1a1, 其中0≤l2≤a1-3.再由a1>3,知l2至少可取两个值. 若l2 若l2=a1-3,则有x+a2-a1=M-(l2-1)a2-(l1+1)a1∈0(x;a1,a2). 这就完成命题4.1的证明. 据此,对于a1>3,我们定义映射η:1(a1,a2)→1(a1,a2)为:如果x∈1(a1,a2),则令 η(x)=max0(x;a1,a2). (4.5) 对于a1=3,我们拓广上述映射为η:1(a1,a2)→(a1,a2)∪{2}: (4.6) 这里q=1时,3q-1=2∉(a1,a2).而x>3q+2r时,皆有η(x)∈1(a1,a2),及(4.5)式成立. 命题4.2如果a3∈1(a1,a2),则当b>η(a3)时,方程 a1x1+a2x2+a3x3=b (4.7) 总存在非负整数解;而当b=η(a3)时,方程(4.7)不存在非负整数解. 证明先考虑a1>3的情形. 当b>η(a3)时,如果b∉1(a1,a2),则b∉(a1,a2),因而存在x1≥0,x2≥0,使得x1a1+x2a2=b.由此知(x1,x2,0)是方程(4.7)的一个非负整数解. 如果b∈1(a1,a2),则由映射η的定义知b∈1(a3;a1,a2),从而有 b=ma3+m2a2+m1a1,m>0,m2≥0,m1≥0. 由此知(m1,m2,m)是方程(4.7)的一个非负整数解. 当b=η(a3)时,有b∈0(a3;a1,a2).如果方程(4.7)存在非负整数解(x1,x2,x3),x3=1将与b∈0(a3;a1,a2)矛盾;x3=0,则得x1a1+x2a2=b,这与b∈1(a1,a2)矛盾.故得,此时方程(4.7)不存在非负整数解. 对于a1=3的情形,只有a3=3q+2r时,产生例外.这时,0(a3;3,a2)=Ø.但在拓广的映射下,当b=η(a3)时,仍有方程(4.7)不存在非负整数解. 命题4.2证毕. 命题4.3对于a1>3,x=M-l2a2-l1a1∈1(a1,a2),映射η的表示形式为: η(x)=max{M-k(l2+1)a2,M-(k-1)(l2+1)a2-(jk+k(l1-Nk)+1)a1}; (4.8) 这里N1=0,j1=0,k≥2时的jk和Nk由(3.17)式定义. η(x)=max{M-(l2+1)a2,M-(l1+1)a1}; (4.9) η(x)=max{M-(l2+1)a2,M-(l1+1)a1}; (4.10) η(x)=max{M-((s+1)l2-s(a1-1)+1)a2-s(l1+1)a1,s=1,…,k-1;M-k(l1+1)a1}. (4.11) 证明由K=K(l2)≥2和(3.16)式可知 K(2+l2)q+2K+Ktr(l2)≤a1q+r-1. (4.12) 据此导出:K(2+l2) 即 r-K(tr(l2)+1)<0. 结合(4.12)式,有 a1q≤K(2+l2)q≤a1q+r-1-(2K+Ktr(l2)) 矛盾!故有:K(2+l2) kx=M-(kl2+k-1)a2-(jk+k(l1-Nk))a1∈1(a1,a2). 而由性质3.6和性质3.4知 (k+1)x=M-((k+1)l2+k)a2-(jk+1+(k+1)(l1-Nk+1))a1∉(a1,a2). 事实上,当k≤K-1时,有(k+1)l2+k≤a1-3;由(3.17)式知jk+1+(k+1)(l1-Nk+1)<0,故由性质3.6得到上式.而当k=K时,如果(K+1)l2+K≤a1-3,则由性质3.6得到上式;如果(K+1)l2+K>a1-3,由性质3.4得到上式. 现在,由kl2+k-1≤Kl2+K-1 kx+(jk+k(l1-Nk))a1-a2=M-k(l2+1)a2∈0(x;a1,a2) 和 kx+l2a2-a1=M-(k-1)(l2+1)a2-(jk+k(l1-Nk)+1)a1∈0(x;a1,a2). 为证明(4.8)式,取y=M-m2a2-m1a1∈1(a1,a2).如果y>M-k(l2+1)a2,则有 (k(l2+1)-m2)a2>m1a1. 由此导出:k(l2+1)-m2>0.记m2=k(l2+1)-i2-1,则有i2≥0.另一方面,由 y>M-(k-1)(l2+1)a2-(jk+k(l1-Nk)+1)a1 可得 ((jk+k(l1-Nk)+1)-m1)a1>(l2-i2)a2. 因此,当0≤i2≤l2时,有(jk+k(l1-Nk)+1)-m1>0.记m1=(jk+k(l1-Nk)+1)-i1-1.由i1≥0,得 y=kx+i2a2+i1a1∈1(x;a1,a2). 而当l2 y>M-((k-2)(l2+1)-1)a2-(jk-1+(k-1)(l1-Nk-1)+1)a1, 从而有 jk-1+(k-1)(l1-Nk-1)+1-m1>(2l2+2-i2)a2>0. 此时记m1=jk-1+(k-1)(l1-Nk-1)-i1.由i1≥0,得 y=(k-1)x+(i2-l2-1)a2+i1a1∈1(x;a1,a2). 一般地,当sl2+s≤i2≤(s+1)l2+s时,s=0,1,…,k-1,由 kx+l2a2-a1>(k-s)x+(l2+s)a2-a1 可得 y>M-((k-s-1)(l2+1)-s)a2-(jk-s+(k-s)(l1-Nk-s)+1)a1, 从而有 jk-s+(k-s)(l1-Nk-s)+1-m1>((s+1)l2+2s-i2)a2≥0. 此时记i1,s=jk-s+(k-s)(l1-Nk-s)-m1.由i1,s≥0,得 y=(k-s)x+(i2-sl2-s)a2+i1,sa1∈1(x;a1,a2). 据此得证(4.8)式. 由K=K(l2)≤1和(3.16)式可知 a2-1<2((2+l2)q+2+tr(l2)), 据此导出l1≤a2-((2+l2)q+2+tr(l2))≤N2. 2x=M-(2l2+1)a2-(j2+2(l1-N2))a1∉(a1,a2), 从而得知 x+l1a1-a2=M-(l2+1)a2∈0(x;a1,a2) 和 x+l2a2-a1=M-(l1+1)a1∈0(x;a1,a2). 为证明(4.9)式,取y=M-m2a2-m1a1∈1(a1,a2).如果y>M-(l2+1)a2,则有 (l2+1-m2)a2>m1a1. 由此导出:l2+1-m2>0.记i2=l2-m2,则有i2≥0.另一方面,由y>M-(l1+1)a1,有 (l1+1-m1)a1>m2a2. 由此导出:l1+1-m1>0.记i1=l1-m1,则有i1≥0.于是得到: y=x+i2a2+i1a1∈1(x;a1,a2). 这就证明了(4.9)式. sx+(a1-l2-2)a2-a1∈0(x;a1,a2), 这里 sx+(a1-l2-2)a2-a1=M-((s+1)l2-s(a1-1)+1)a2-s(l1+1)a1, 以及 kx+(kl2-(k-1)(a1-1))a2-a1=M-k(l1+1)a1∈0(x;a1,a2). 注意到x>a2,导出(a1-l2-2)a2>(l1+1)a1,进而得知: M-l2a2=x+l1a1 为证明(4.11)式,取y=M-m2a2-m1a1∈1(a1,a2).由 y>x+(a1-l2-2)a2-a1>M-l2a2 有 (l2-m2)a2>m1a1. 由此导出:l2-m2>0,从而0≤m2≤l2. 现在,如果0≤m2≤kl2-(k-1)(a1-1),记i2=kl2-(k-1)(a1-1)-m2,则有i2≥0.另一方面,由y>M-k(l1+1)a1,有 (k(l1+1)-m1)a1>m2a2. 由此导出:k(l1+1)-m1>0.记i1=k(l1+1)-1-m1,则有i1≥0.于是得到: y=kx+i2a2+i1a1∈1(x;a1,a2). 如果对于s=1,…,k-1,有(s+1)l2-s(a1-1)+1≤m2≤sl2-(s-1)(a1-1),则由 y>sx+(a1-l2-2)a2-a1=M-((s+1)l2-s(a1-1)+1)a2-s(l1+1)a1 可得 (s(l1+1)-m1)a1>(m2-((s+1)l2-s(a1-1)+1))a2≥0. 由此导出:s(l1+1)-m1>0.记i1,s=s(l1+1)-1-m1,则有i1,s≥0;同时记 i2,s=sl2-(s-1)(a1-1)-m2, 则有i2,s≥0.从而导出: y=sx+i2,sa2+i1,sa1∈1(x;a1,a2). 这就证明了(4.11)式. 至此命题4.3得证. 本节,我们给出G(a1,a2,a3)的表示形式.注意到方程(1.1)变成 a1x1+a2x2+a3x3=b, (5.1) 其中 a1 (5.2) 显然地,有 G(1,a2,a3)=G(1,a2)=0. (5.3) 故以下总设a1>1,并分两种情况来讨论. 定理5.1如果(a1,a2)=1,则当a3∉1(a1,a2)时,有 G(a1,a2,a3)=G(a1,a2); (5.4) 而当a3∈1(a1,a2)时,有 G(a1,a2,a3)=η(a3)+1. (5.5) 证明当a3∉1(a1,a2)时,仅须证明当b=G(a1,a2)-1时,方程(5.1)没有非负整数解.如果成立a3>b,则这是显然的.如果a3 a1(x1+x3t1)+a2(x2+x3t2)=b=a1a2-a1-a2. 这与a1a2-a1-a2∈1(a1,a2)相矛盾!故得证(5.4)式. 当a3∈1(a1,a2)时,由命题4.2得到(5.5)式.定理证毕. 定理5.2如果(a1,a2)=d>1,则有 G(a1,a2,a3)=d×(G(c1,c2,a3)-1)+(d-1)a3+1, (5.6) 其中ai=cid,i=1,2,而G(c1,c2,a3)由定理5.1所定义. 证明令b=d×(G(c1,c2,a3)-1)+(d-1)a3.先证明此时方程(5.1)没有非负整数解.如若不然,便有xi≥0,i=1,2,3,使得 a1x1+a2x2+a3x3=d×(G(c1,c2,a3)-1)+(d-1)a3, 此即 d(c1x1+c2x2)+a3(x3-d+1)=d×(G(c1,c2,a3)-1). 由(5.2)式,有d c1x1+c2x2+a3t=G(c1,c2,a3)-1. 矛盾!故此时方程(5.1)没有非负整数解. 现在,对于b>d×(G(c1,c2,a3)-1)+(d-1)a3,我们来构造方程(5.1)的非负整数解.记 b=d×(G(c1,c2,a3)-1)+(d-1)a3+td+i, (5.7) 其中t≥0,0 b=d×(G(c1,c2,a3)-1+t+k+nq)+a3(d-1-n). 由G(c1,c2,a3)-1+t+k+nq>G(c1,c2,a3),可知存在ti≥0,i=1,2,3,使得 c1t1+c2t2+a3t3=G(c1,c2,a3)-1+t+k+nq. 因此,(t1,t2,t3d+d-1-n)是方程(5.1)的一个非负整数解. 至此定理5.2得证. 注意到依据公式(1.4),有G(d,a3)=(d-1)(a3-1),我们可以将上述两个定理的结论整合成一个公式: (5.8) 这里(a1,a2)=d,ai=cid,i=1,2. 现在,我们来证明本文的主要结果. 首先,我们将映射η:1(a1,a2)→1(a1,a2)的结果符号改记为η(x;a1,a2)=η(x).并仿此推广到一般的情形.设(a1,…,ak)=1.令 0(a1,…,ak)={x;x∈(a1,…,ak),x (6.1) 1(a1,…,ak)={x;x∈(a1,…,ak),x>ak}. (6.2) 再对于x∈1(a1,…,ak),令 (6.3) 0(x;a1,…,ak)=(a1,…,ak)1(x;a1,…,ak), 并定义映射η:1(a1,…,ak)→1(a1,…,ak)为: η(x)=η(x;a1,…,ak)=max0(x;a1,…,ak). (6.4) 据此,我们将定理5.1推广到一般情形. 定理6.1如果(a1,…,ak-1)=1,则当ak∉1(a1,…,ak-1)时,有 G(a1,…,ak-1,ak)=G(a1,…,ak-1); (6.5) 而当ak∈1(a1,…,ak-1)时,有 G(a1,…,ak-1,ak)=η(ak;a1,…,ak-1)+1. (6.6) 证明当ak∉1(a1,…,ak-1)时,仅须证明对于b=G(a1,…,ak-1)-1,方程(1.1)没有非负整数解.如果ak>b,(x1,…,xk)是方程(1.1)的非负整数解,则有xk=0.因此有 a1x1+…+ak-1xk-1=G(a1,…,ak-1)-1,xi≥0,i=1,…,k-1. 这与G(a1,…,ak-1)的定义相矛盾! 如果ak ak=a1t1+…+ak-1tk-1. 假如此时方程(1.1)有非负整数解(x1,…,xk),则有 a1(x1+t1xk)+…+ak-1(xk-1+tk-1xk)=G(a1,…,ak-1)-1. 这同样与G(a1,…,ak-1)的定义相矛盾! 当ak∈1(a1,…,ak-1)时,如果b=η(ak;a1,…,ak-1),则方程(1.1)没有非负整数解.如若不然,设(x1,…,xk)是方程(1.1)的非负整数解.则xk>0使得b=a1x1+…+akxk∈1(ak;a1,…,ak-1)与b=η(ak;a1,…,ak-1)=max0(ak;a1,…,ak-1)相矛盾!故xk=0,因而有 a1x1+…+ak-1xk-1=b. 这与b∈1(a1,…,ak-1)相矛盾! 如果b>η(ak;a1,…,ak-1),则方程(1.1)总有非负整数解.事实上,若b∉1(a1,…,ak-1),则有b∉(a1,…,ak-1).因而存在整数ti≥0,i=1,…,k-1,使得b=a1t1+…+ak-1tk-1.于是,(t1,…,tk-1,0)是方程(1.1)的一个非负整数解. 若b∈1(a1,…,ak-1),则有b∈1(ak;a1,…,ak-1),即于是,(m1,…,mk-1,m)是方程(1.1)的一个非负整数解. 定理6.1得证. 定理6.2如果(a1,…,ak-1)=d>1,则有 G(a1,…,ak)=d×G(c1,…,ck-1,ak)+G(d,ak), (6.7) 其中ai=cid,i=1,…,k-1. 本定理的证明与定理5.2的证明完全类似,从略. 将上述两个定理整合,可以得到一个表示公式: (6.8) 其中(a1,…,ak-1)=d,ai=cid,i=1,…,k-1. 据此,我们便可以递推地给出定理1.2的证明.过程是平凡的,从略. 注记6.3我们对于k>3的情形,略去了映射η(ak;c1,…,ck-1)的表示形式,因为它太繁琐冗长,从命题4.3就可见一斑.或许它存在简洁的形式,只是我们未能发现,就留给有兴趣的读者吧!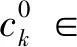
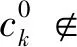
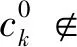

2 一个基本引理
3 非负不可解集(a1,a2)的若干性质



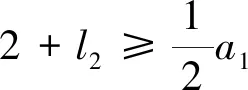
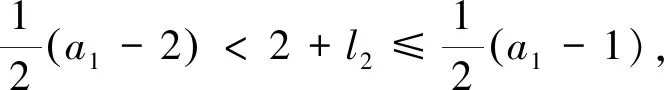

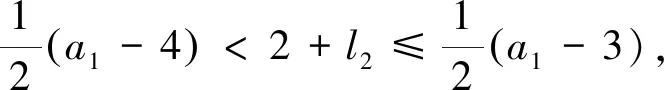
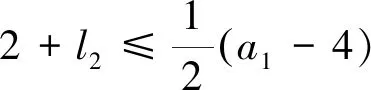
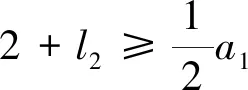
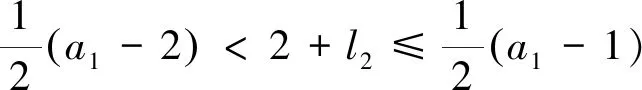


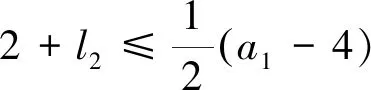


4 不可解集1(a1,a2)上的一个自映射
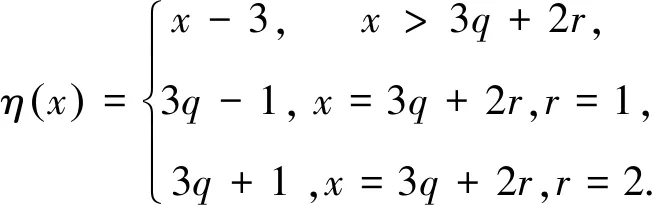
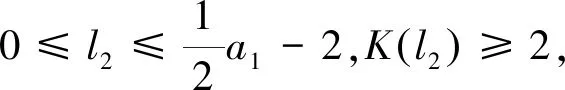


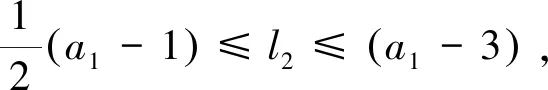



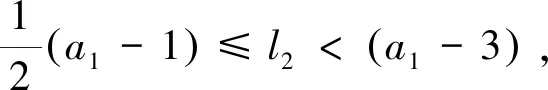
5 G(a1,a2,a3)的表示形式
6 定理1.2的证明

