矢量控制交流电动机调速系统的Simulink仿真

尚 丽

(苏州市职业大学 电子信息工程学院，江苏 苏州 215104)

变频调速是现代异步电动机交流调速系统中最主要的调速方式[1-3]。但是，在三相静止坐标系下的异步电动机的动态数学模型具有高阶非线性的多变量强耦合特征，常用的恒压频比控制、转差频率控制的变频调速方法静态性能较好，但在动态特性、低速转矩特性方面，仍不如直流电动机[1-3]，故其应用范围受到限制。而交流电动机结构简单、应用广泛、维护方便而高效的优点又远优于直流电动机，因此，随着交流调速技术的发展，矢量控制异步电动机变频调速方法便应运而生[4-6]，该方法最早由德国学者K.Hass和F.Blaschke在20世纪70年代提出，其实际是一种解耦和控制，目的是把复杂的异步电动机数学模型等效为直流电动机的数学模型，简单方便地实现异步电动机的变频调速。经过多年发展，矢量控制技术已比较成熟[7-9]，目前较典型的有转差频率矢量控制、气隙磁场定向的矢量控制、定子(转子)磁场定向的矢量控制等。但是，矢量控制技术的理论知识比较复杂，工程实际应用时如果借助于仿真技术可以使调速系统调试更方便，更易于排除故障和避免故障的发生。应用于教学中，更易于学生理解矢量控制系统的组成及其工作原理，对调速结果有了更加直观的认识和理解，有助于提高教学效果。因此，本文采用Matlab/Simulink仿真平台实现转子磁场定向的异步电动机转速闭环矢量控制调速的建模，给出主要仿真模块的建模方法和参数设置，并在给定的转速和磁链下对仿真结果进行分析和讨论。

1 矢量控制变频原理

1.1 坐标变换

矢量控制技术就是借助坐标变换，将异步电动机的控制模型等效变换成直流电动机的控制模型，其等效原则是：在不同坐标系下的电动机模型产生的磁动势相等。把静止的定子三相电流ia，ib，ic经坐标变换为静止的两相电流iα，iβ后，用控制器产生按转子磁链定向坐标系中的定子电流励磁分量id和转矩电流分量iq给定值，即i和，经过逆矢量变换得到三相电流给定值，然后通过电流闭环控制，输出异步电动机调速所需的三相定子电流，从而调节电机的磁通和转矩以达到调速的目的。静止三相定子交流电流ia，ib，ic等效成两相静止电流iα，iβ的变换如下[10-12]：

而两相静止坐标系α-β变换为两相旋转坐标系d-q的关系如下：

因此，根据以上两式推出如下的定子三相电流变换到转子旋转坐标系上的两相电流id，iq(即3s/2r变换)及其反变换(2r/3s变换)的关系如下[6-7]：

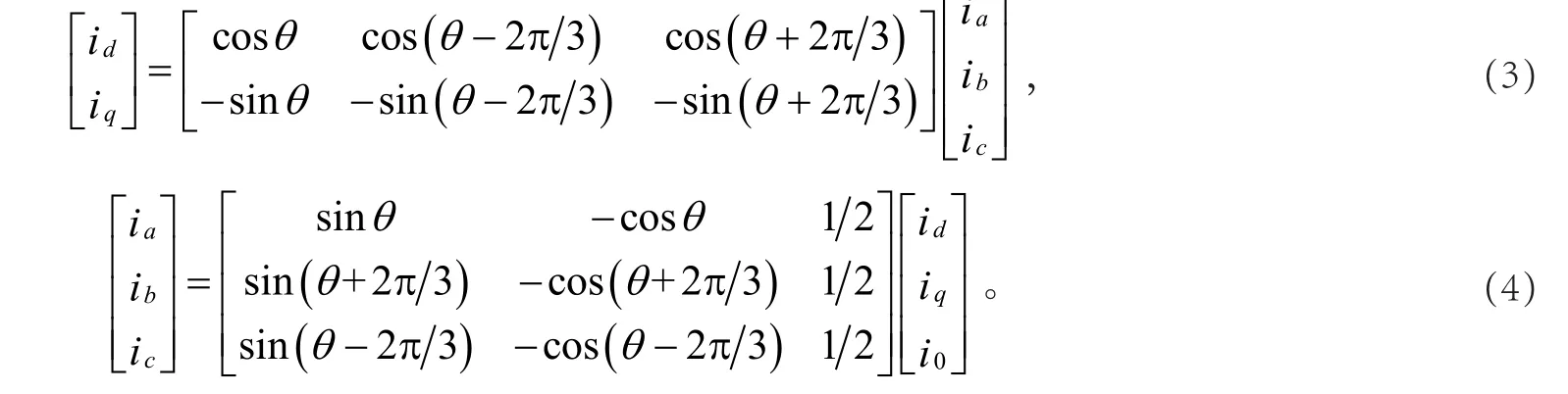
1.2 异步电动机矢量控制原理

根据坐标变换思想，一台异步电动机经过3s/2r变换后，再经过矢量旋转变换器(vector rotator，VR)，即可变成一台由励磁电流(直流)分量id和转矩电流(直流)分量iq为输入，转速ω为输出的等效直流电动机，模仿直流电动机的控制策略，得到直流电动机的控制量，经过相应的坐标反变换2r/3s，就能够控制异步电动机[8-10]。根据上述描述，异步电动机矢量控制系统的原理图如图1所示。图1中，Ψ是转子给定磁链值，ω⋆是给定角速度。

图1 异步电动机矢量控制系统的原理图

在同步旋转dq坐标系中，把d轴方向固定在转子磁场方向，故矢量控制也称为磁场定向控制。当异步电动机为鼠笼式结构时，由于转子短路，则在d轴和q轴方向上的转子电压udr=uqr=0，电压方程的矩阵形式为：

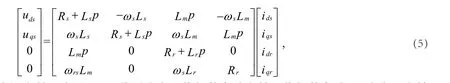
式中：Rs，Rr分别为定子电阻和转子电阻；Ls，Lr分别为定子绕组的自感和转子绕组的自感；Lm为定子和转子绕组间的互感；ωs为定子角速度；ωsr为转差角频率；p为微分算子；uds，uqs分别是d轴和q轴上定子电压分量；ids，idr和iqs，iqr分别为d轴和q轴上定子和转子的电流分量。由于在矢量控制中，主要控制的是定子电流分量，故推导出和定子电流相关的关系式如下：

式中：Tr=Lr/Rr为转子励磁时间常数；Ψrd为转子磁链在d轴上的分量；Te为转矩；Ψr为转子磁链；np为极对数。令ωsr为转差角频率，则其推导如下[5-8]：

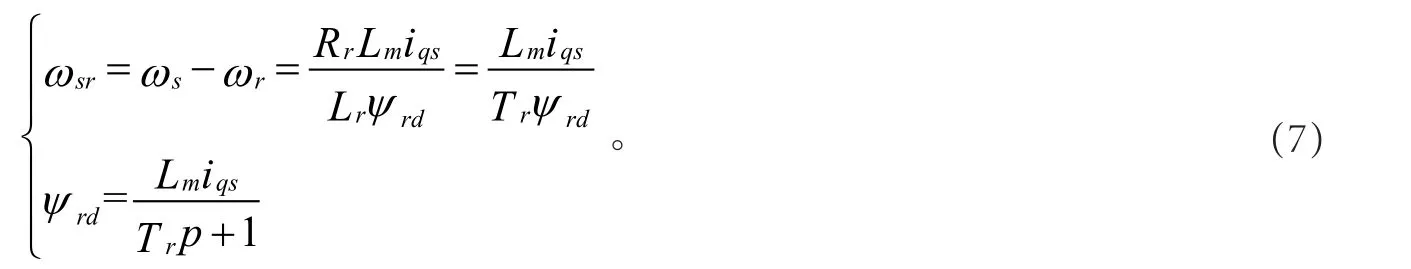
式(6)和式(7)构成了异步电动机以同步转速旋转的转子磁场定向的矢量控制基本方程，其实现了定子电流励磁分量与转矩分量的解耦，转子磁链在d轴分量Ψrd仅由定子电流励磁分量ids决定，当转子磁链达到稳态并保持不变时，电磁转矩Te仅由定子电流转矩分量ids决定。因此，根据被控系统的性能要求给定ids和iqs的值，就可以实现调速系统转矩的实时控制了。

1.3 矢量控制系统的结构和工作原理

根据闭环控制规律，得到转子磁场定向控制的转速闭环、转矩闭环和磁通闭环的矢量控制系统结构图，如图2所示。系统主要包括的功能模块如下：转速调节器(automatic speed regulator，ASR)、电流滞环调节器(automatic current regulator，ACR)、转矩和磁通计算模块、同步旋转坐标的旋转角度计算模块、三相定子电流转换为两相电流(即等效为励磁电流和转矩电流)模块及其两相转换为三相定子电流逆变换模块，电流滞环比较PWM控制模块、异步电动机模块等。其中ASR、转矩环均采用比例—积分(proportion integration，PI)控制规律，实现转速和转矩的无静差控制。电流滞环模块由滞环控制器和逻辑非运算器组成。当给定转速ω⋆与实测转速ω比较后送入ASR，得到转矩指令与磁链估计值Ψr经iqs计算模块得到转矩电流分量转子磁链给定值经过ids计算模块得到定子电流的励磁分量和经过逆旋转变换和两相到三相变换获得定子电流指令值，与实测三相电流经过ACR控制产生PWM逆变器的脉冲触发信号，从而控制异步电动机的运行，实现矢量变频控制调速的目的。

图2 矢量控制系统结构图

2 主要模块的仿真建模

2.1 矢量控制系统的仿真模型

根据矢量控制系统的电气工作原理和图2所示的结构图，采用Matlab/Simulink中的仿真工具构建如图3所示的矢量控制系统仿真模型。系统主要包含封装好的异步电动机—逆变器模块、矢量控制模块。其中矢量控制模块包括三相和两相坐标变换模块、磁链及转子磁链角计算模块、电流滞环模块、转速PI调节模块等。此外，仿真模型加入了示波器模块以便观察转速、转矩以及磁链的波形。

图3 矢量控制系统仿真模型

2.2 异步电动机—逆变器仿真模块

异步电动机选择SimPowerSystems库中的鼠笼式异步电动机，逆变器模块选择3桥臂6脉冲触发的全控桥式IGBT模块。异步电动机与逆变器连接的仿真模型及其封装后的图形如图4所示。异步电动机的三相定子绕组A、B、C与IGMT的输出A、B、C对应相连，异步电动机的输入负载为Tm，输出为总线信号m，包含了定子电流、转子电流、转矩、转速等信号。IGBT的脉冲信号g为6路PWM控制信号，由电流滞环控制模块得到。

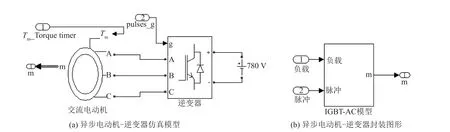
图4 异步电动机-逆变器仿真模型及其封装图形

2.3 矢量控制仿真模块

矢量控制模块的仿真模型及其封装图形如图5所示。其主要由以下模块的封装图形组成：三相到两相(3s/2r)坐标变换模块、两相到三相(2r/3s)坐标变换模块、转子磁链相位角θ计算模块、电流滞环模块、磁链计算模块、励磁电流和转矩电流计算模块等。

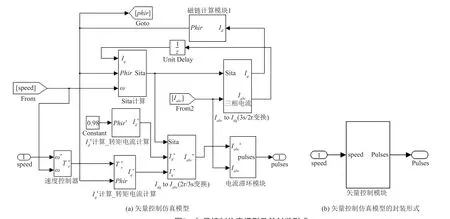
图5 矢量控制仿真模型及其封装形式

2.3.1 3s/2r变换仿真模块

三相静止坐标系abc到两相旋转坐标系dq的变换仿真模型的内部结构如图6所示。其中id和iq模块中的函数表达式分别如式(8)和式(9)所示。

式中：u[1]=sinθ，u[2]=cosθ，u[3]=ia，u[4]=ic，u[5]=id，θ=ωt。

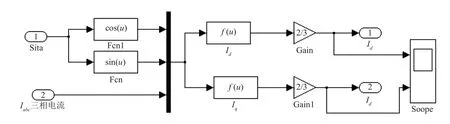
图6 三相到两相坐标系变换的仿真模型（3s/2r变换）

2.3.2 2r/3s变换仿真模块

转子磁场定向的两相旋转坐标系dq到三相静止坐标系abc变换的仿真模型内部结构如图7所示。由于本文采用的异步电动机是三相无中线连接的鼠笼式异步电动机，则有ia+ib+ic=0，即ic=-ia-ib。图7中ia和ib的f(u)函数表达式分别如式(10)和式(11)所示。

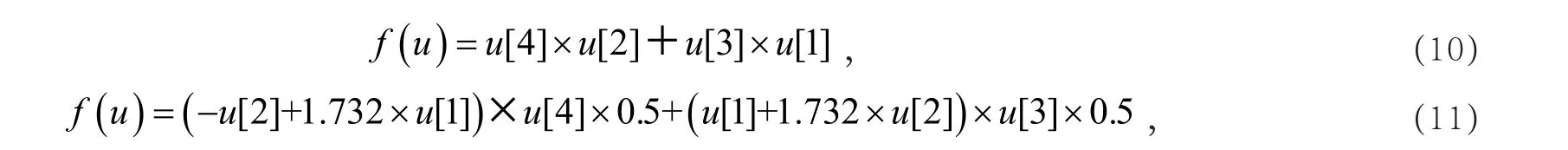
式中：u[1]=sinθ，u[2]=cosθ，u[3]=iq，u[4]=id。

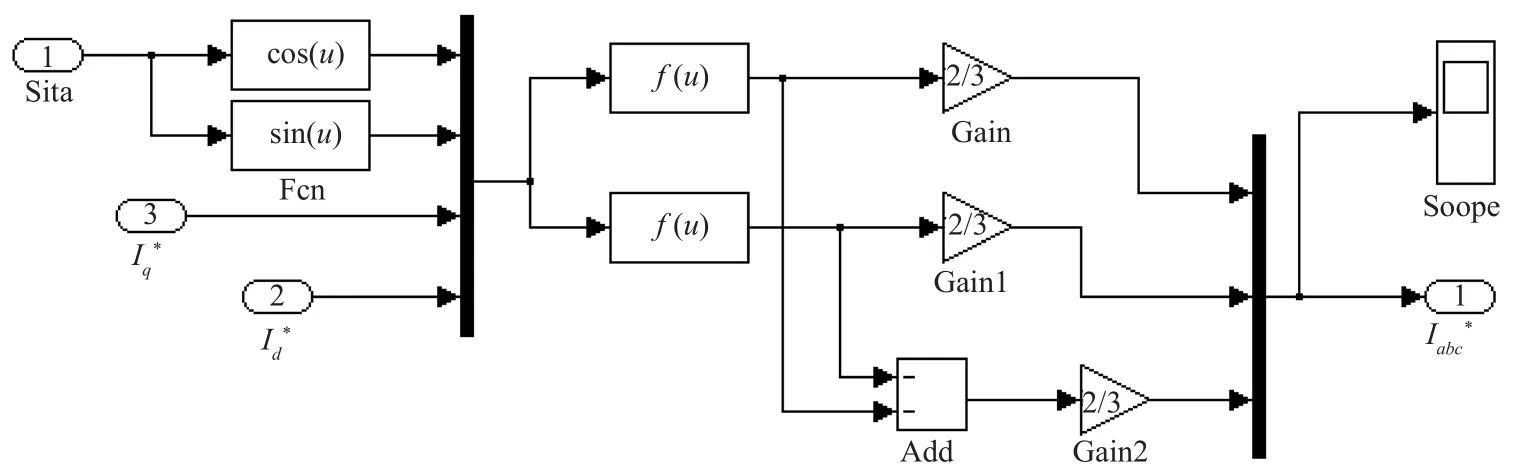
图7 两相到三相坐标系变换的仿真模型（2r/3s变换）

2.3.3 电流滞环仿真模块

电流滞环控制模块的仿真模型如图8所示。该模块由3个滞环控制器和3个逻辑非运算器组成，其输入信号为三相指令电流值和三相实测电流值，输出6路IGBT逆变器控制信号。通过控制逆变器的通、断来调节逆变器输出线电压的频率，从而实现调速的目的。减小滞环宽度，可以减小输出相电流的纹波，但是环宽不能太小，以免功率器件的开关频率加大，引起电流超调，增大跟踪误差，降低电流的控制精度。

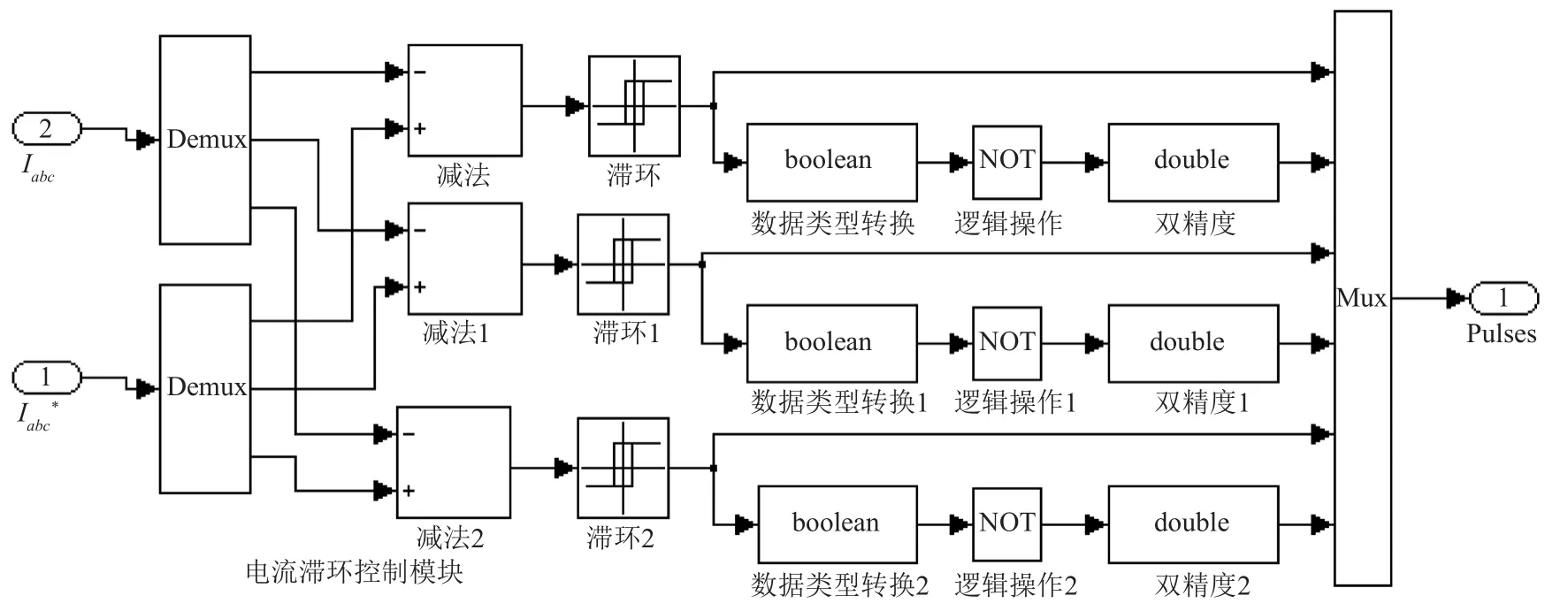
图8 电流滞环控制模块的仿真模型

2.3.4 转子磁链及磁链角计算模块

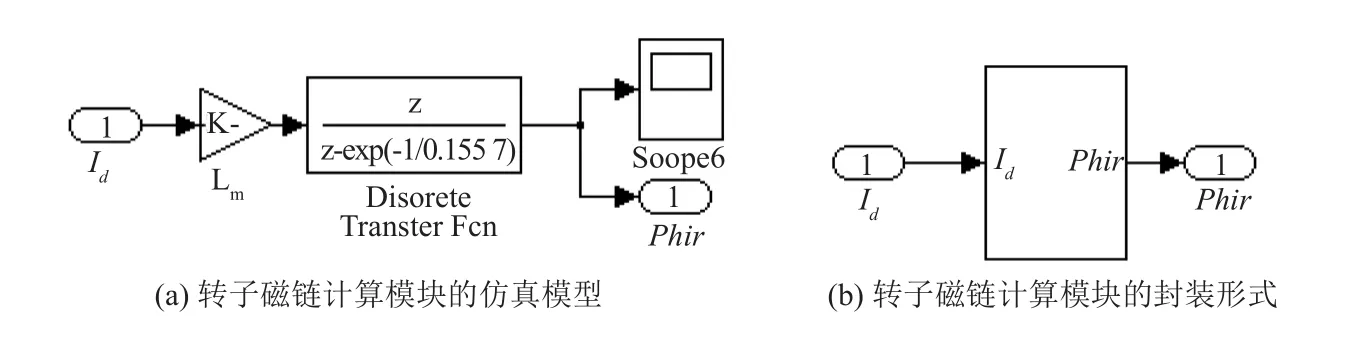
图9 转子磁链计算模块的仿真模型及其封装形式

转子磁链在动态过程中恒定不变是关键因素，其精度直接影响调速系统的动态性能。利用定子电流的励磁分量可以计算出转子磁链幅值，其磁链计算模块内部结构及其封装形式如图9所示。转子磁链角的仿真模型及其封装形式如图10所示。根据转矩电流分量iq和检测磁通Ψr的值，由式(7)可以得到转差频率ωsr，把ωsr与实测的转子转速ωr相加可以得到定子频率信号ωs，再经过积分环节即可得到转子磁链角θ。通过计算θ角，可以实现转子磁场定向。图10模块中，iq=u[1]，Phir=u[2]，则函数f(u)的表达式为

图10 转子磁链角的仿真模型及其封装形式

2.3.5 励磁电流和转矩电流计算模块

励磁电流计算模块的仿真模型及其封装形式和转矩电流计算模块的仿真模型及其封装形式分别如图11和图12所示。根据式(6)和式(7)得到给定的和分别计算如下：

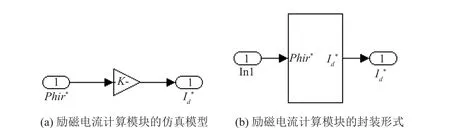
图11 励磁电流计算模块的仿真模型及其封装形式

图12中，函数f(u)的表达式为

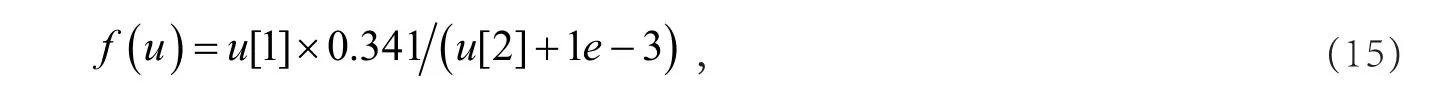
式中为了避免转子磁场初值为零，出现奇异点发散现象，使得系统稳定性增加，加入了一个常数0.001。

2.3.6 速度控制模块

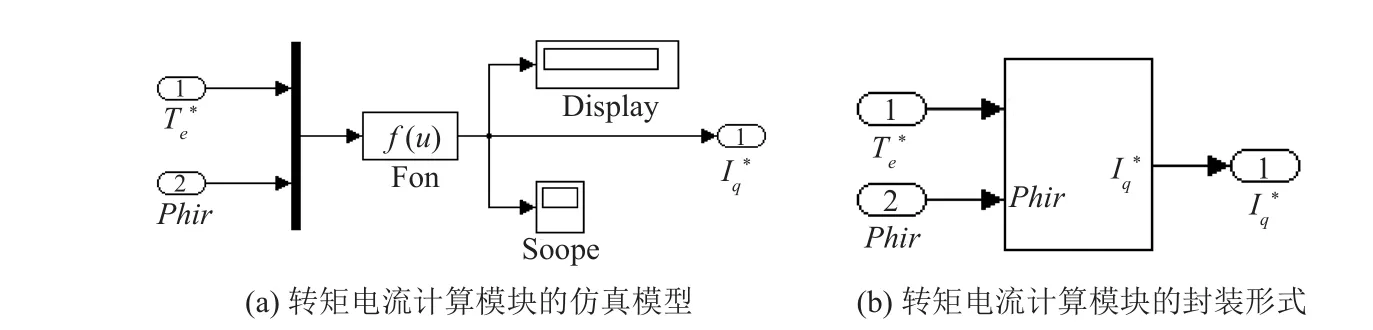
图12 转矩电流计算模块的仿真模型及其封装形式

速度调节采用带有限幅作用的PI控制器，其表达式为

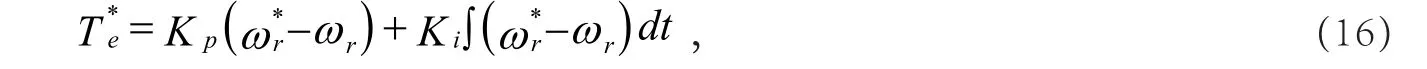
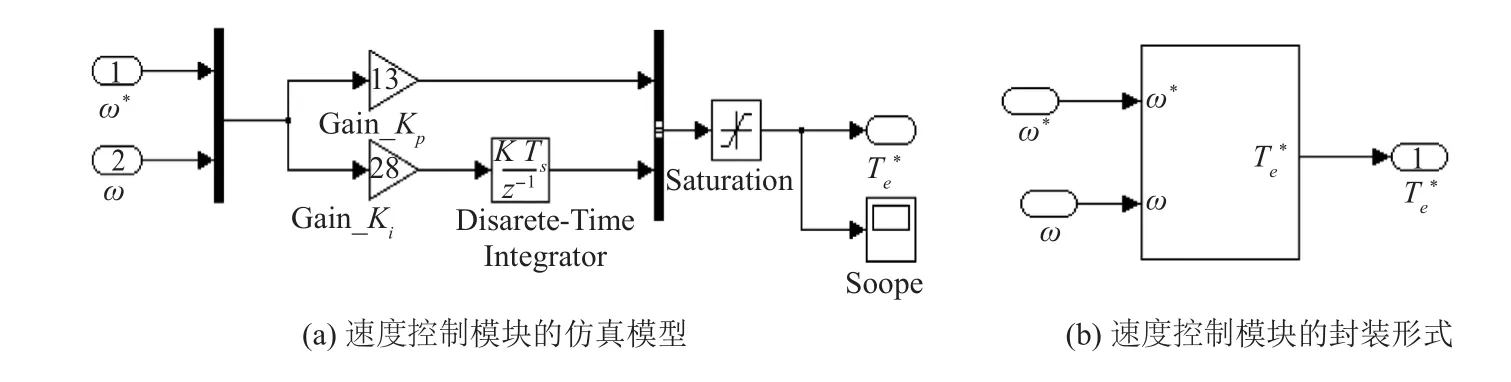
图13 速度控制模块的仿真模型及其封装形式

3 仿真结果与分析

3.1 主要仿真模块测试

根据图3所示的仿真模型，设置仿真时间为5 s，选择电动机的定子三相电流、电动机的电磁转矩T以及转子角速度ω作为测量对象，另外采用电压测量模块检测电动机的三相线电压。下面对主要模块参数设置和功能测试进行讨论。

3.1.1 PWM逆变和交流电动机模块的调试

首先对交流电动机模块和PWM逆变模块进行联调测试。主要参数选择为：额定功率PN=3 700 W；线电压380 V；额定频率50 Hz；定子内阻Rs=0.087 8 Ω；转子内阻Rr=0.228 Ω；定子漏感Ls=0.8 mH；转子漏感Lr=0.8 mH；互感Lm=34.7 mH；极对数np=2；转动惯量J=0.663 kg.m2。逆变模块的直流电压设为650 V。设置好相应的仿真参数后，对异步电动机和逆变器模块进行调试，通过编程得到的仿真波形如图14所示，波形变化趋势和理论分析相一致。

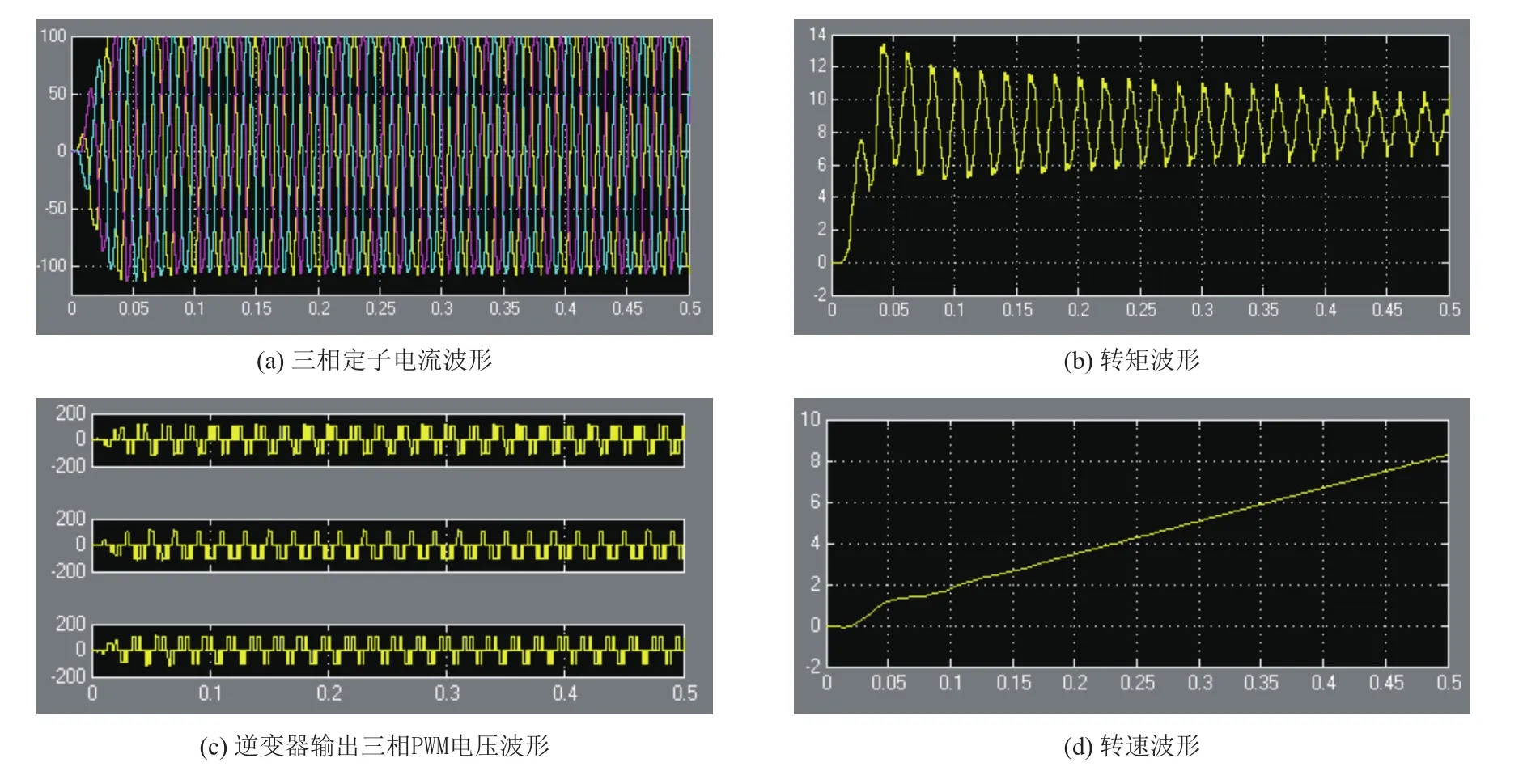
图14 异步电动机—逆变器模块仿真测试波形

3.1.2 坐标变换模块的调试

任意设置三相和两相正弦信号的幅值和频率，测试坐标系相互变换模块的功能，观测示波器得到的仿真波形如图15所示，其中信号幅值大小为2，频率为50 Hz。结果显示模块功能正确。

3.1.3 滞环电流模块的调试

滞环电流控制器的滞环环宽2 h影响电流跟踪控制的精度。环宽较大时，功率开关器件的开关频率可降低，但是电流的谐波分量大；环宽较小时，电流波形失真较小，但是功率器件的开关频率会变大。仿真测试中，三相电流信号的幅值为20，电流滞环模块的电流环宽2 h为10。以A相电流信号如图16(a)，和A相电流的偏差信号如图16(b)作为滞环控制器的输入信号，经滞环控制器作用后分配给逆变器的脉冲信号如图16(c)所示，利用该脉冲控制功率器件IGBT的开通和关断，得到A相滞环逆变后的电流波形如图16(d)所示。同样地，对B相和C相电流进行测试也得到类似的波形，仅相位和A相电流依次相差120˚。仿真结果表明，所构建的电流滞环控制器模块是正确的。

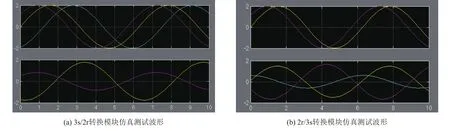
图15 三相和两相坐标系转换模块仿真测试波形（坐标变换旋转角度θ=60°）

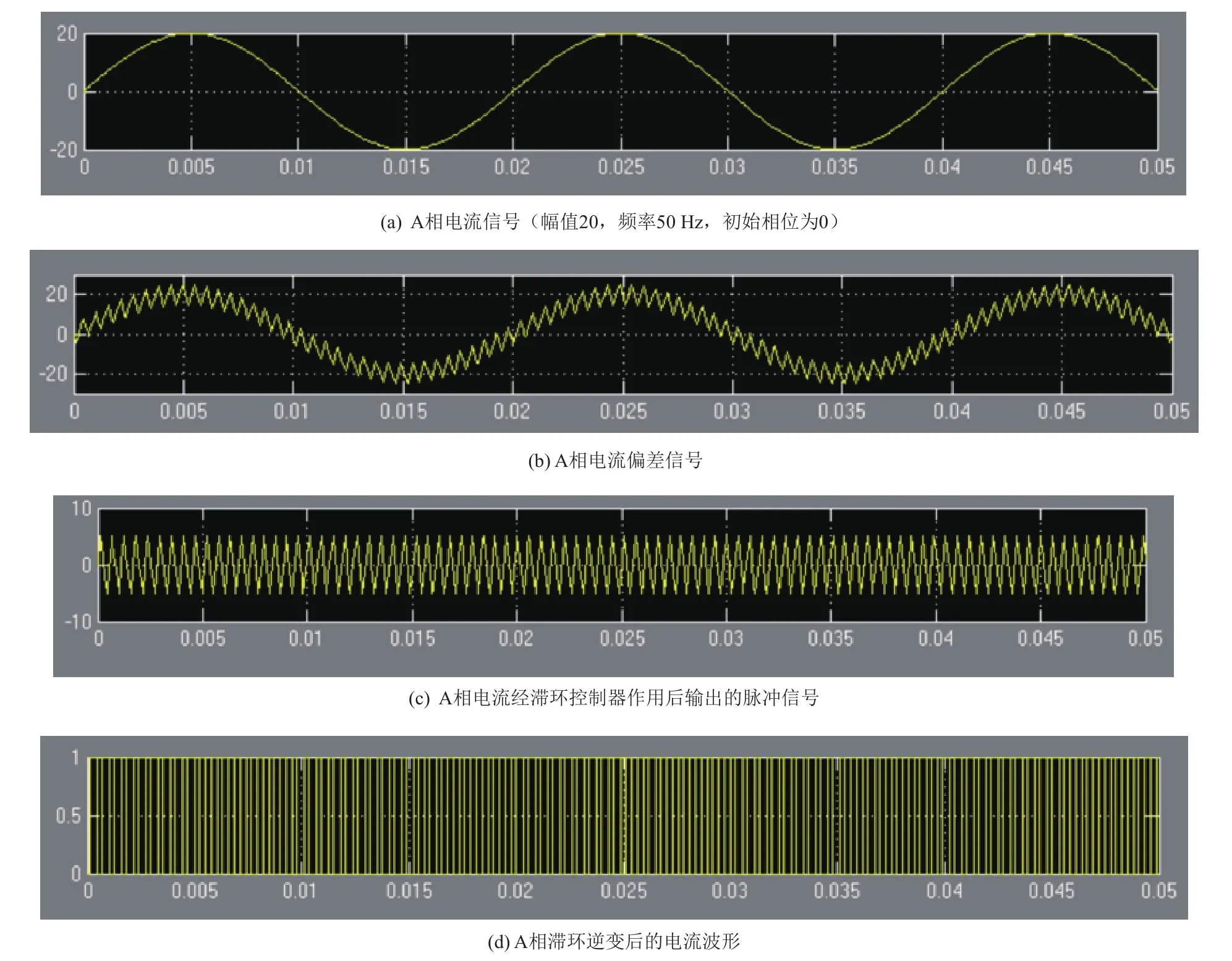
图16 以A相为例对电流滞环控制模块测试得到的仿真波形

3.2 仿真结果分析

根据3.1节内容，已知本文所构建的主要模块仿真测试都是正确的。对图3所示的矢量控制系统的仿真模型按照3.1节中参数设置的方法进行讨论。在异步电动机的测量模块Demux中选择转子角速度、定子三相电流、电磁转矩作为输出信号接到仿真示波器端，以便直观地观测到相应的仿真波形。滞环电流环宽为20 A，转速给定信号设为120 rad/s，转速调节器ASR的积分放大倍数K设为26，比例放大倍数Kp设为13。当空载启动时，三相定子电流和转速仿真波形分别如图17(a)和图17(b)所示。由图17可知，电动机空载起动的瞬间，定子电流突然增加，接近300 A，转速迅速增加，超过给定的转速值，持续时间约0.45 s， 1.5 s后转速达到稳态值120 rad/s。

考虑带载启动时得到的转速仿真波形如图17(c)所示。设电动机初始负载为50 N·m，当转速达到稳定值后，在2 s时加入100 N·m的负载时，可以观测到转速突然下降，但很快又回到转速的给定值，说明系统有较好的抗干扰性能。

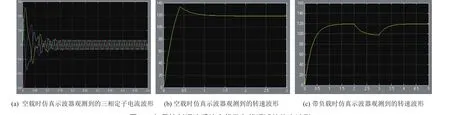
图17 矢量控制调速系统空载及负载调试的仿真波形

4 结论

在分析矢量控制调速系统的组成和工作原理的基础上，讨论了该系统的Simulink仿真建模过程，对系统中主要模块的参数进行理论分析和计算，设置了较合理的仿真参数并通过仿真实验测试了每一个功能模块的正确性。对矢量控制调速系统在空载启动、带载启动加扰动情况下的系统动、静态性能进行了仿真，仿真结果表明，在恰当选取仿真参数时，系统的动态响应快、超调量较小，有一定的抗干扰能力，从而验证了本文所构建模型的正确性和有效性。得到的仿真结果用于教学环节时，可以帮助学生较直观地理解矢量控制的异步电动机调速系统的工作原理。此外，仿真结果对该系统的实际工程设计也有一定的借鉴意义。