迭代函数系统(IFS)法的分形图形技术在丝绸纹样上的应用

朱海祥，刘 婧，戴绘瑶，卞毓颖，宗 林

(1.苏州市职业大学 教育与人文学院，江苏 苏州 215104；2.苏州吴绫丝绸精品有限公司，江苏 苏州 215005)

1 研究背景

分形图形具有自相似和自仿射的特点，可以无限表达图形的精细结构，是描述大自然的几何语言，很多在欧氏空间中无法描述的现象，用分形理论可以得到很好的解释[1]。许多自然分形和数学分形都可以利用迭代函数来生成，如迭代函数系统(iterated function system，IFS)和复函数迭代等。只需几组仿射变换系数就可以基本确定一个分形图形的IFS生成方法，采用该方法可生成千变万化而又具有高分辨率结构的分形图形。图案设计是丝绸纹样设计的难点，传统的图案设计难以创新突破，而且难以修改。近年来，分形图形在纺织方面的应用逐渐增加，但更多聚焦在J集和M集上，IFS分形图形由于创作的周期长和个性化特点，在图案设计方面应用IFS分形图形相关研究较少。通过IFS分形图形的函数和变换设计，结合分形图案的生成特点和数码喷射印花技术，可以实现其在丝绸纹样上的个性化应用和订单式生成，为IFS分形图形从设计到应用提供新的思路。

2 IFS分形图的生成原理

IFS分形图的生成主要分成两个阶段，一是构造分形图所需要的若干压缩仿射变换群；二是确定仿射变换群后计算机软件的实现。仿射变换是二维坐标之间的线性变换，变换须满足式中：a，b，c，d，e，f为实系数；x，y为未知数。IFS生成法基于这个思想，认为几何对象的整体和局部在仿射变换的意义下具有自相似结构，因此可以通过定义对象的整体并选定若干仿射变换，将整体形态变换到局部，通过反复迭代过程直至得到满意的图形[2]。复杂的IFS分形图形生成以拼贴原理为基础，经过若干仿射变换的多次压缩作用，形成具有自相似特点的分形图。以Apophysis分形软件为例来讨论分形图形的计算机生成原理，绘制图形主要根据以下三个步骤：①随机选择一个位置后，随机选择一个变换作用在该位置上，生成一个新的位置；②随机选择一个变换作用在新的位置上，重复若干次后，得到第一个点；③随机选择一个变换作用在第一个点上，反复进行可生成一个点序列，最后再回到第一步重复这个过程，即可根据所选择的仿射变换生成对应的分形图形。这里要注意的是初始仿射变换的个数必须大于等于2，若有初始函数，则作用在对应的仿射变换之后[3]。

3 IFS分形图的生成与优化

3.1 基本分形图的生成流程

经典的数学分形有希尔伯特曲线、科赫曲线、谢尔宾斯基地毯、Cantor三分集、门格海绵、莱维C形曲线、H树、龙形曲线、庞加莱圆盘模型等，这些都可以利用不同软件来生成。ISF 将待生成的图像看成是许多与整体相似或经过一定的变换与整体相似的局部小块(子图) 拼贴而成，每个子图都是整体图形的一个仿射变换[4]。以谢尔宾斯基地毯为例，利用Apophysis分形软件来描绘其生成过程涉及的基本仿射变换及其IFS码。

谢尔宾斯基地毯的IFS三角变换如表1所示。软件一般以任意图形为初始图形，对其施加表1中的8个压缩仿射变换wi(i=1，2，…，8)，进行反复迭代，生成谢尔宾斯基地毯及其仿射变换图如图1所示。谢尔宾斯基地毯对应的IFS码如表2所示。

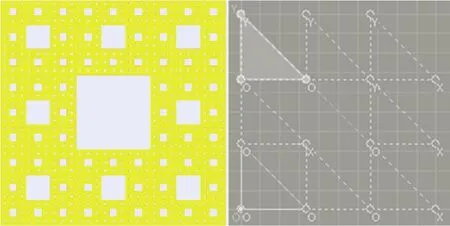
图1 谢尔宾斯基地毯及其仿射变换图

表1 谢尔宾斯基地毯的IFS三角变换

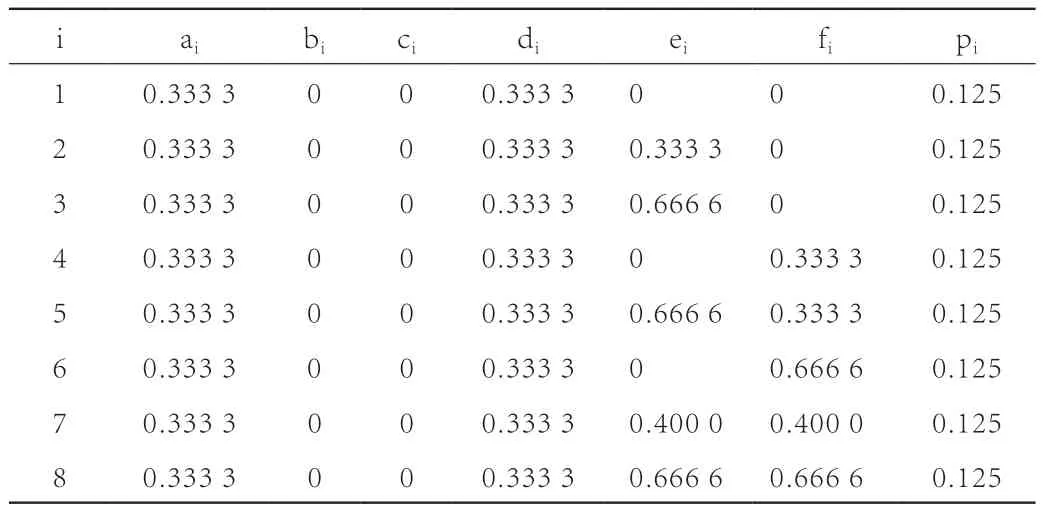
表2 谢尔宾斯基地毯分形的IFS码

3.2 一般分形图的生成流程

除了经典数学分形外，自然界存在许多自然分形，如树木、花草、山脉、云层等，这些分形的数学构建，主要是根据自相似的特点进行目标图形分解，发现每部分对应的压缩仿射变换来实现的。为了设计出更具特色和精细效果的分形图形，还可以结合Apophysis分形软件自带的函数、Xaos、颜色渐变条等内置功能进行更有实用性的艺术创作。现以图2中分形蝴蝶为例，分析其形成过程中的各项功能选择和设置。该分形图包括8个压缩仿射变换wi(i=1，2，…，8)，进行反复迭代，对应的IFS码如表3所示。为了图形更具艺术效果和实用价值，在绘图过程汇总并添加了下面的变化函数，如其中另外还可以对图形的颜色、结构、位置作进一步的调整和优化，得到如图2所示的分形蝴蝶。

图2 分形蝴蝶

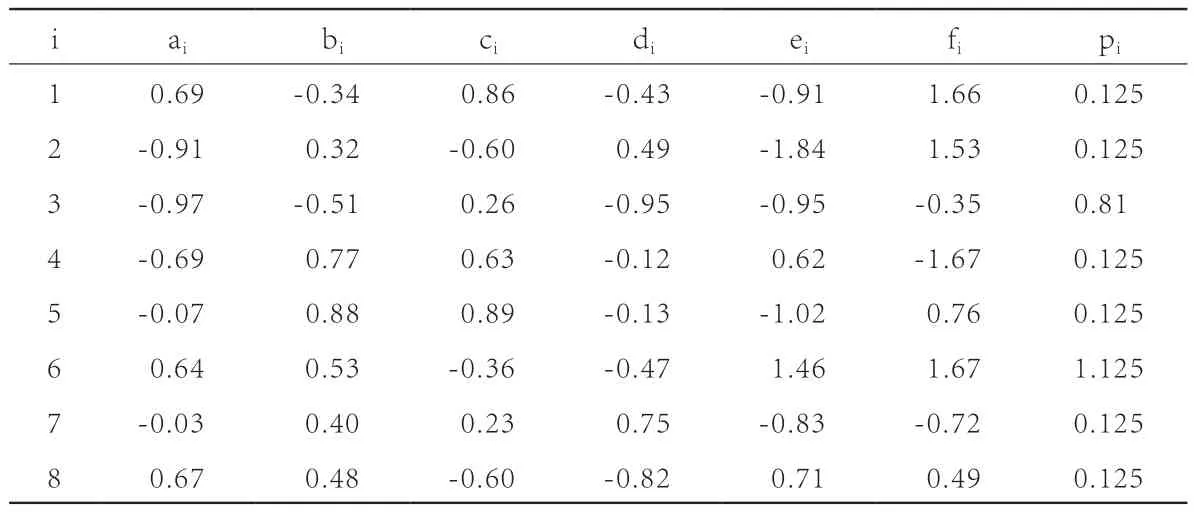
表3 分形蝴蝶的IFS码

图3中分形花包括4个压缩仿射变换wi(i=1，2，3，4)和若干变化函数，进行反复迭代。表4为对应的IFS码，变化函数包括等，其中：

图3 分形花

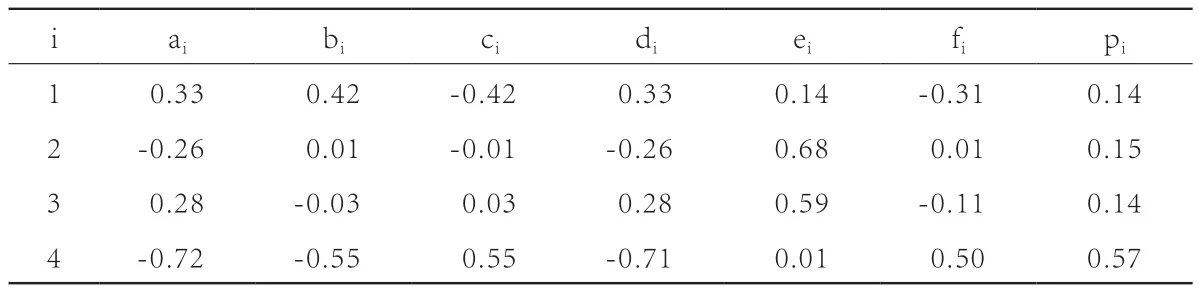
表4 分形花的IFS码

图4中玫瑰束包括5个压缩仿射变换wi(i=1，2，3，4，5)和若干变化函数，进行反复迭代。表5为对应的IFS码，变化函数包括等，其中

图4 玫瑰束

表5 玫瑰束的IFS码

图5中蓝莲花包括4个压缩仿射变换wi(i=1，2，3，4)和若干变化函数，进行反复迭代。表6为对应的IFS码，变化函数包pre_blur、zcale、julia3D。

图5 蓝莲花

表6 蓝莲花的IFS码

4 IFS分形图的印花实验

根据分形图形具有无限精细结构和色彩绚丽的特点，结合所需要的主题，选择图形中的基本元素，同时进行人工干预，根据市场的需求和生产的要求对图案进行不断调整，设计符合要求的原始图案后进行输出。一方面提供的分形图形必须具有较高的像素，这样在印制的过程中，才可以保证产品画面细节的清晰度；另一方面，可以根据丝绸面料的特点选择不同的分形图形进行二次处理，生成一些二方连续纹样、四方连续纹样等，转化为具有较高应用价值的纺织纹样，满足不同的生产需求，如图6所示。

图6 分形蝴蝶的丝绸纹样

以图3中的分形花为例，在真丝面料上进行实验，选择真丝雪纺和真丝素绉缎两种不同的真丝面料。先对8姆米的真丝雪纺炼白胚进行试验，这种面料是平纹组织结构，成分是100%桑蚕丝，具有透明、柔软、飘逸等特性。以原始图形底色为朦胧轻盈的图形，希望在同样清透的面料上产生飘逸的效果，同时凸显图案和面料的特点。又对12姆米的素绉缎面料炼白胚进行试验，素绉缎是指一类全真丝的、纬线强捻(2 600捻)、经线不加捻、织物组织为五枚缎的真丝缎类品种。这个面料的成分是100%桑蚕丝，特点是亮丽的缎面非常高贵，手感滑爽，富有弹性，组织密实，可以充分展现图形的精细程度。图3选择的是有非常精细的结构，希望在不透明的素绉缎面料上可以展示朦胧底色上精细流畅顺滑的线条，同时肥亮的缎面可以将图案的色彩衬托得更加鲜明。

在图案的印制方式上，采用的是八色的超精细数码喷射印花机，两个专色，六个常规色，将图形调整至90 cm×90 cm的大小之后进行印制。印制前还有一个必须的上浆过程，将真丝雪纺面料和素绉缎面料进行上浆处理，由此可以保证面料的平整度和上色效果，然后才能上机印制。在面料下机进行后道整理之后就可以看到面料成品，具体见图7、图8。之后将面料进行裁剪卷边就可以得到一条完整的围巾。

图7 素绉缎平铺效果图

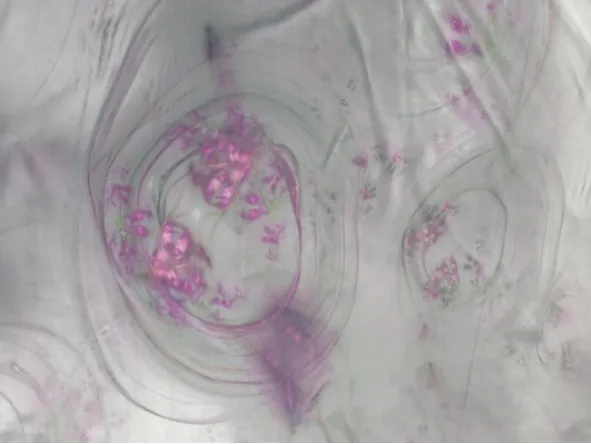
图8 雪纺平铺效果图

根据实验得到的效果，提出在实际应用过程中，一方面需要提高导出图形的像素，增加图案的精细程度，同时降低原始图案的底色灰度增加透亮感；另一方面利用图形拼接软件产生连续纹样。另外还可以扩大面料的选择面，尝试不同厚度以及品种的真丝面料，力求最大程度展现图案和面料的特色，达到两者的最佳契合度。

5 结论

利用IFS法生成仿射变换群，可以模拟生成形态各异的自然分形和数学分形，既具有分形的复杂性特点，又具有自然物体(植物树、树叶等)的基本形态，同时具有数字化的基本特征[5]。在每个仿射变换中都可以添加适合的函数和颜色渐变，形成更加绚丽多彩、无限精细结构的应用型分形图形，在此基础上结合分形图案的生成特点和数码喷射印花技术，实现分形图形在丝绸纹样上的应用。