2018 年全国卷Ⅱ第21 题的解法探究与分析

江苏省盱眙中学 张 勇

函数是高中数学的重要内容，历年的高考试题都涉及大量的函数知识，而其中导数解答题常处于压轴题的位置，难度较大，意在考查考生的运算求解能力、化归转化思想以及数学运算和逻辑推理的核心素养。

一、真题再现

该题结果简洁精炼，第一问考查常规具体三次函数的单调性，较简单，第二问表述虽极其简单，但重点考查函数的零点问题，如何通过函数零点存在定理说明函数零点的存在性与唯一性。

二、解法探究

第（1）问较常规，过程如下：

第（2）问解法探究如下：

解法一：

故g（x）只有一个零点。综上，f（x）只有一个零点。

此方法从函数g（x）着手寻找零点所处位置，关键在于寻找较g（x）大的函数和较g（x）小的函数

解法二：

在解法一的基础上，g（x）至多有一个零点，从而f（x）至多有一个零点。也可以从函数f（x）着手寻找零点所处的位置。

这里说明为什么取3a-1 和3a+1，事实上，取满足上述条件的值均可，如可知等。

解法三：

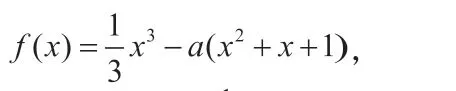
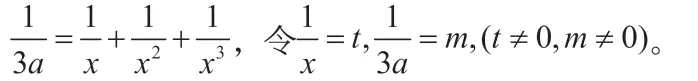
综上，f（x）只有一个零点。

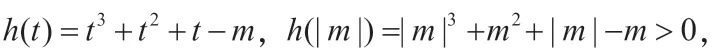
综上，f（x）只有一个零点。

解法四：

?

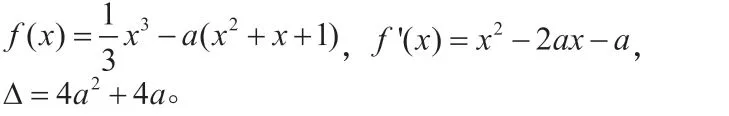
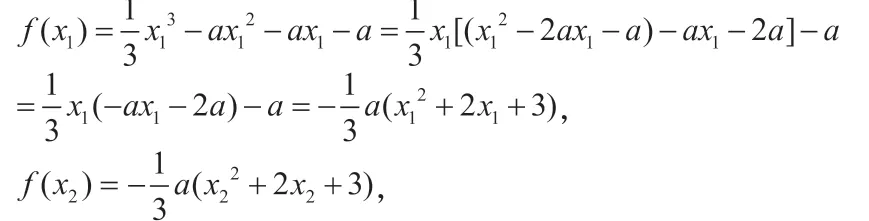
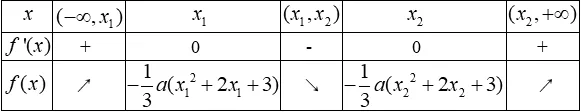
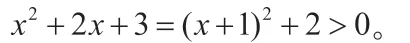
综上，f（x）只有一个零点。

此方法通过讨论三次函数的单调性和极值，利用极值点代换来判断函数极值的正负。