最小二乘拟合的MEMS加速度计简易标定方法

王学瀚

（温州职业技术学院 电气电子工程系，浙江 温州 325035）

0 引 言

微机电系统（Micro Electro Mechanical Systems，简称MEMS）传感器和嵌入式处理器的快速发展，促进了低成本航姿参考系统（Attitude and Heading Reference System，简称AHRS）的可能性[1-3]。AHRS使用多种传感器通过相应数据融合算法进行工作，加速度计作为其主要传感器之一起稳定姿态的作用，其测量精度直接影响AHRS整体性能。受MEMS制造工艺和工艺员等因素的影响，MEMS加速度计输出受多项误差源影响[4-5]。加速度计在使用之前，有必要建立相应确定性误差模型对输出进行有效标定补偿，其本质是建立输入输出模型并计算出该模型中的系数矩阵。文献[6-8] 借助高精度转台和复杂标定路径分别设置6位置、12位置和24位置标定法，通过比较MEMS加速度计各轴输出值与当地的重力加速度值，计算出加速度计确定性误差补偿参数。分立式标定方法有良好的标定结果，但因需要借助外界专业设备而局限于实验室环境，无法满足现场标定需求。为此，文献[9-10] 提出简易标定方法，无需借助外界设备，利用伪观测信息建立Kalman滤波方程，动态估计出加速度计零偏和标度因数。然而，该方法具有针对性、复杂性的参数调整，使得该方法难以实现传感器的普适性，进而伪观测信息方法要求MEMS加速度计在运动过程中外部加速度和位置变化近似为“0”，难以在实际场景中得到严格保证。本文依据MEMS加速度计输出模型，提出一种无需借助任何外界设备、无需参数设置、具有普适性的标定方法，要求加速度计绕原地有效旋转，采集多余加速度信息，并通过最小二乘法求解出相应的系数矩阵，实现加速度计标定补偿系数矩阵的求取。

1 加速度计输出分析

MEMS加速度计性能的指标与其误差源存在一定关系。为更好地完成加速度计确定性误差标定与补偿，考虑影响MEMS传感器性能的三项主要误差源，即零偏误差、标度因数误差和非正交误差[11]。零偏误差是指当输入数值为“0”情况下MEMS加速度计输出值，零偏误差每次启动都不相同，时间间隔越长变化越大，可通过传感器使用手册中零偏稳定性、零偏重复性等反映。标度因数误差是实际值与标定数值之间的差值，反映为MEMS加速度计输出值与输入值之间的比例系数，通常影响因素主要包含标度因数不对称性、标度因数非线性度等。非正交误差由于制造工艺等因素影响，MEMS加速度计真实输入轴与理想三轴之间不完全重合，存在小角度偏差。这些误差源系数随着MEMS加速度计的使用次数的增加或存放时间的推移而变化，因而通常需要将MEMS加速度计进行半年或三个月一次的定期标校，以确定其补偿系数或在MEMS加速度计每次使用之前进行标定。综合考虑加速度计各项误差，建立真实加速度Ae和量测值Am之间的误差模型关系，即：

其中，K= diag (KxKyKz)，表示标度因数误差引起的比例系数表示非正交误差带来的影响；ρ,φ,λ表示小角度对应的三角函数的近似值；o=[oxoyoz]T，表示零位误差带来的影响。则MEMS加速度计真实值Ae为：

其中，B=(K×T)-1，表示因标度因数误差和非正交误差耦合产生的混合系数；B表示一个上三角矩阵。

2 最小二乘拟合

手持MEMS加速度计在原地旋转时，其线速度几乎为零，理论上加速度计输出值为当地的重力矢量在传感器三轴的投影，满足幅值为定值的约束不变。由文献[12] 可知，原地旋转的MEMS加速度计输出轨迹是三维空间中的圆球面。但MEMS加速度计实际输出会受到多项误差源的影响，作用后的输出轨迹产生形变，满足椭球面约束。（3）式为（2）式加速度计真值的2-范数的平方，其推导过程为：

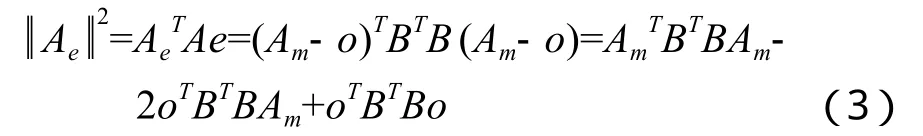
其中，符号“‖ ‖”为向量的2-范数，将其整理为二次型，简记为：

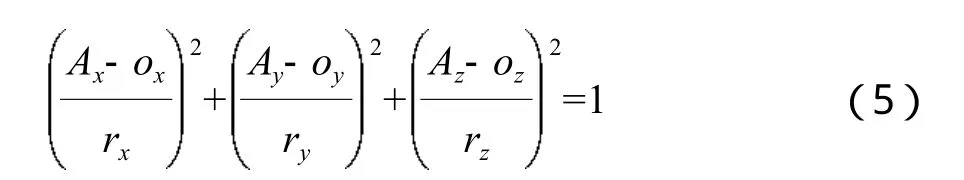
其中，rx,ry,rz为非正交误差、标度因数和重力约束幅值耦合后的系数，几何意义上分别代表赤道半径和极半径。

由（4）式或（5）式可看出，受多项误差影响的加速度计输出满足三维空间的椭球约束。理论上建立6组相互独立的方程式可唯一确定其系数。顾及一般性，建立多组（≥6）方程组可通过最小二乘法求出最佳逼近系数。为此，以下分两步进行：

第一步，假定椭球体的赤道半径和极半径大致相等，即rx=ry=rz=r，这种假定在不考虑非正交误差的影响下成立。将（5）式展开，并简记为：

（6）式可表述为离散数据的最佳逼近问题，按误差平方和最小的原则求取系数，即：

法方程为：

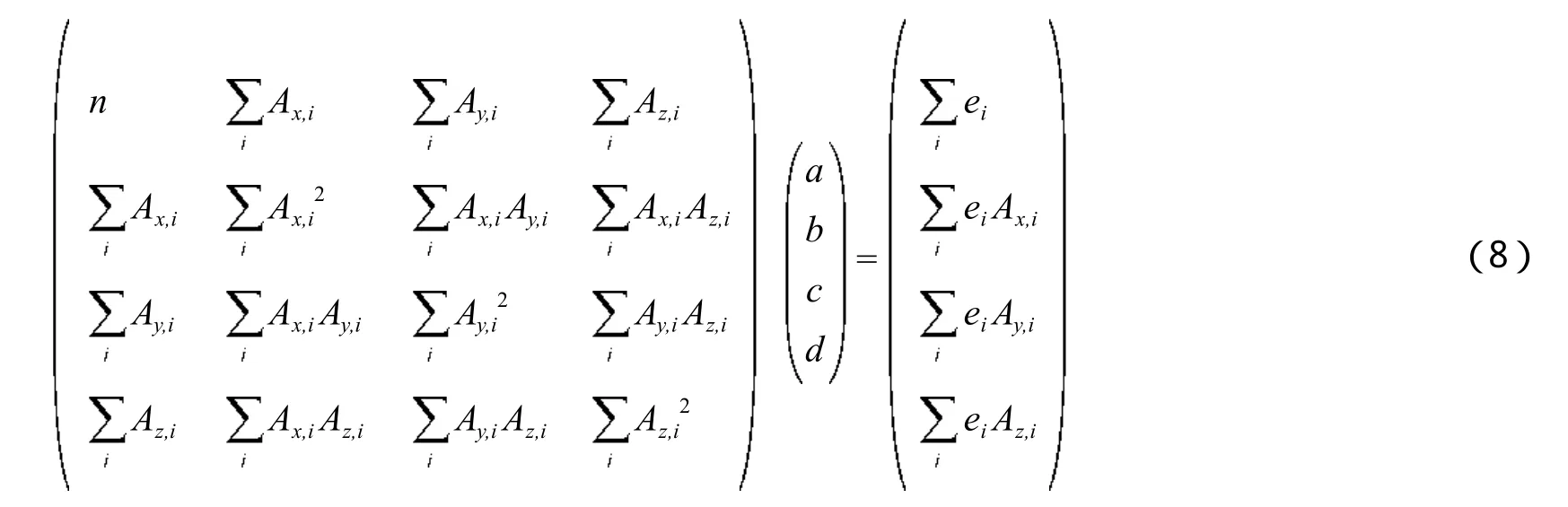
结合（8）式，对于精度要求不高的MEMS加速度计应用而言，可用椭球体最大半径r代替赤道半径和极半径，即：

第二步，在考虑赤道半径和极半径不相等的条件下，将（5）式简记为：

同样， （10）式也采用最小二乘法，按误差平方和最小的原则求取系数，即：

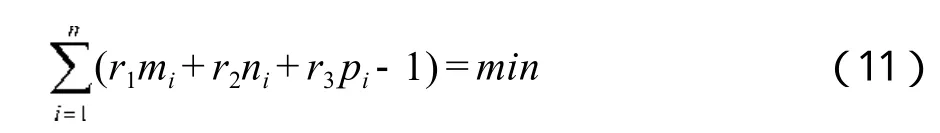
法方程为：

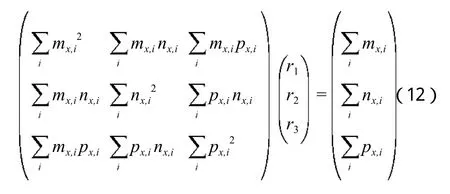
设置采样频率，将MEMS加速度计绕原地旋转，观测多组（≥6）数据，得到基于最小二乘法逼近拟合的标定系数，它具有计算量小、运行速度快的特点。

3 实 验

3.1 分立式标定实验

为验证标定方法的可行性和有效性，选用Xsens公司生产的MTi-G-710传感器，分别开展传统分立式标定实验和基于最小二乘法原地旋转标定实验。传统分立式标定方法需要以三轴惯导试验转台为基础，通过六位置实验完成对MTi-G-710误差模型系数的确定。将MEMS传感器的轴向与三轴转台的中心轴线垂直安装，设置5min采样时间及0.01s采样间隔；启动三轴转台实现六位置转换采样，在某一位置采样前需要将传感器预热2min，采样后对仪器进行断电，待恢复至室温转换至下一位置，采集数据通过串口传至PC端，基于MATLAB环境编写六位置标定程序。加速度计静态标定六位置各轴指向如图1所示。

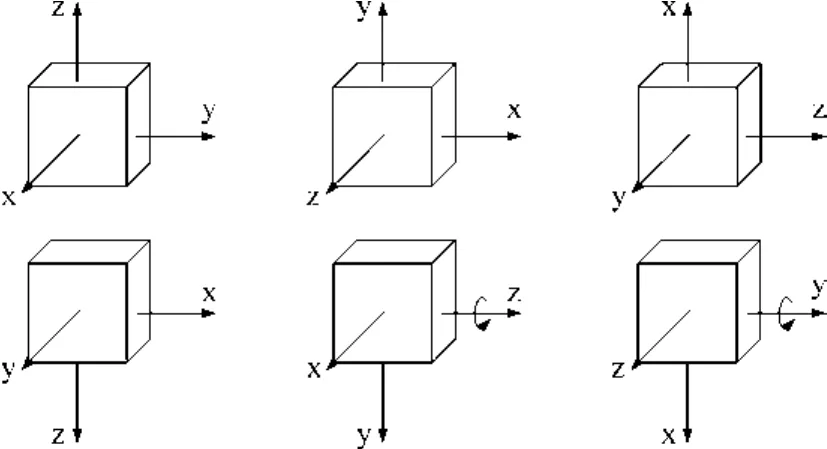
图1 加速度计静态标定六位置各轴指向

按上述实验方法，选用Xsens公司生产的MTi-G-710传感器，开展10次六位置标定实验，分立式加速度计标定结果见表1。

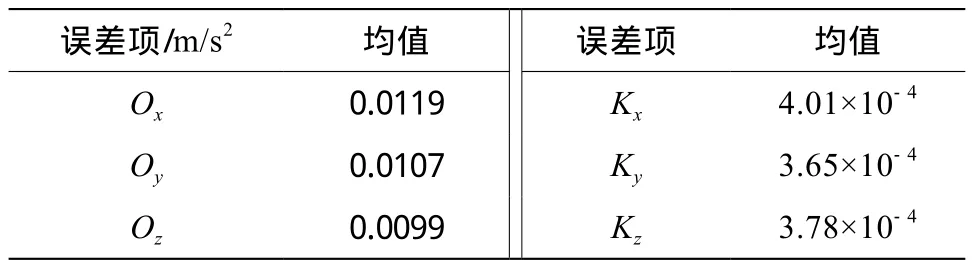
表1 分立式加速度计标定结果

3.2 旋转式标定实验

受三轴转台限制，分立式标定方法只能在实验室开展。在实际工程应用中，考虑到实验人员现场标定的实际需求，开展原地旋转式标定实验。MTi-G-710传感器设置相同的采样间隔，通电预热2min，然后开始原位旋转，绕传感器三个敏感轴采集不同角度多组数据，传感器旋转时使数据尽可能多地分布在椭球面上。两种手持传感器旋转方式如图2所示。

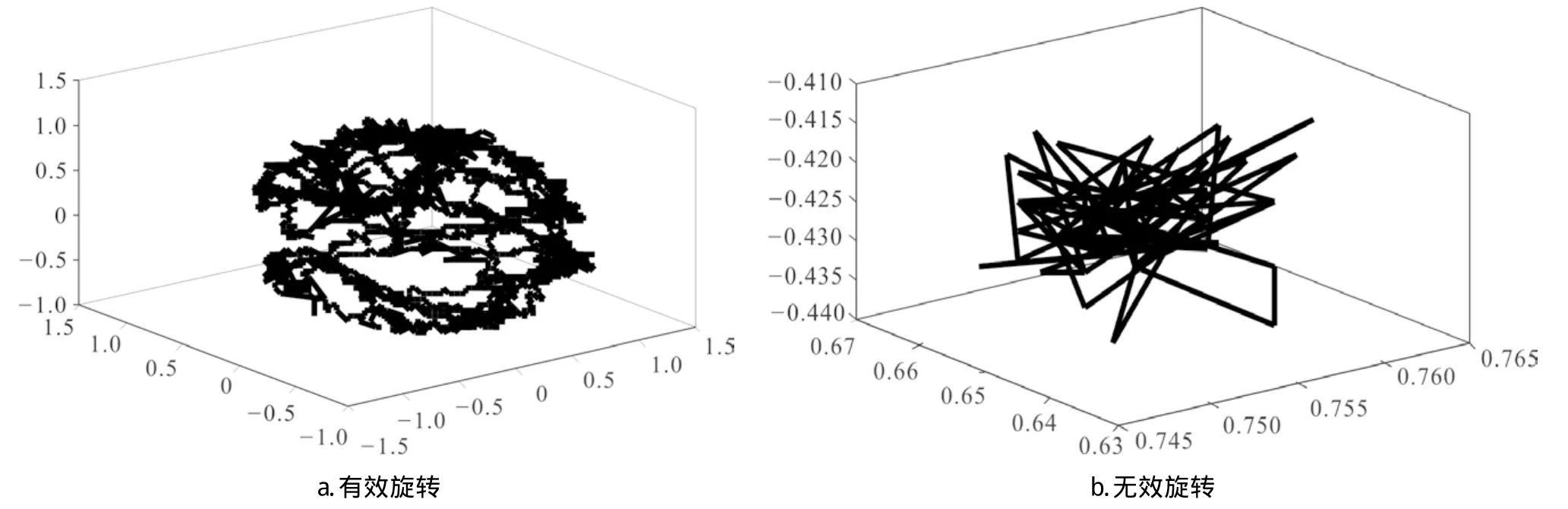
图2 两种手持传感器旋转方式

采集的数据通过串口导入PC端，利用MATLAB编写最小二乘拟合的加速度计标定程序。求出x轴、y轴、z轴零位误差分别为0.011 76m/s2、0.014 7m/s2、0.018 6m/s2，求出椭球赤道半径和极半径分别为0.039、0.035 7、0.047。

3.3 静态、动态输出验证

为进一步说明标定方法的有效性，将3.2中最小二乘法得到的标定系数分别对静态、动态加速度计输出进行补偿。

将MTi-G-710传感器静止置于平面，统计标定前后加速度计输出频数直方图（见图3）。由图3可知，标定前加速度计受多项误差源影响，其输出值离散分布于0.92～1.07g，标定补偿后加速度计输出呈正态分布，均值为1g，验证了标定方法计算的补偿系数在静态模式中有效。

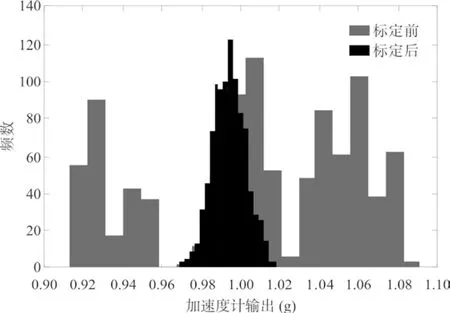
图3 标定前后加速度计输出频数直方图

将MTi-G-710传感器开启航姿仪模式。选择输出已标定的陀螺仪数据和未标定的加速度计数据，将3.2中各项误差改正系数补偿加速度计输出，依据文献[14] 中扩展Kalman姿态融合算法，建立自适应的加速度计量测噪声的协方差矩阵，更新姿态矩阵，开展动态AHRS实验，求取姿态信息。以商用软件MT Manager4.7的解算结果为参考姿态，得到姿态解算相对误差结果如图4所示。由图4可知，横滚角误差、俯仰角误差及航向角误差均在0°附近，且横滚角平均误差低于1.23°，俯仰角平均误差低于1.31°，稳定后（以50s为稳定时间）水平角误差低于1°；航向角平均误差低于5.18°，稳定后（以50s为稳定时间）航向角平均误差低于3°，满足低成本纯惯性AHRS解算精度要求，验证了加速度计标定系数在动态模式中有效。

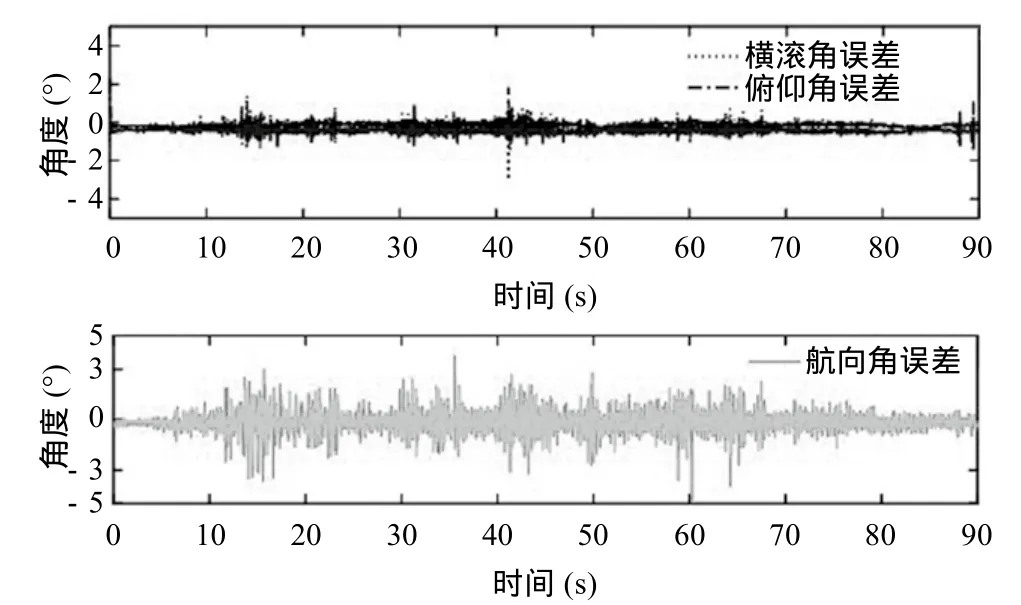
图4 姿态解算相对误差

4 结 论

零偏误差、标度因数误差和非正交误差是影响MEMS传感器性能的三项主要误差源。本文提出将MEMS加速度计绕原地有效旋转，基于最小二乘法得到加速度计确定性误差补偿系数的简易标定方法。该标定方法无需重复迭代计算，无需借助专业标定设备，无需设置复杂参数，可在1min内快速确定标定补偿系数。与传统分立式标定进行实验比较，以验证零偏标定的有效性，由于该标定方法将非正交误差、标度因数及加速度计真值约束模值耦合而成，无法与经典式结果比较。为验证该标定方法补偿系数的可行性和有效性，分别开展静态输出和动态AHRS实验，结果表明，该标定方法可用于实际外场标定场景。