时滞依赖于状态的脉冲中立型随机发展积分微分方程温和解的存在性

黄 浩，王良龙

(1.合肥师范学院数学与统计学院，安徽合肥230601；2.安徽大学数学科学学院，安徽合肥230039)

积分微分方程可以对生物学、化学动力学、电力学、流体力学等许多领域中的问题进行建模。近年来，确定型的Volterra型积分微分方程由于其很强的应用性而备受关注，一些学者利用预解算子理论研究其温和解的存在性和可控性，获得了一系列结果[1-3]。此处的预解算子与抽象空间中微分方程的发展算子在形式上类似，但由于其不满足半群性质，因此本质不同。

Sakthivel[1]考察了式(1)形式的非线性发展积分微分方程

借助预解算子理论和不动点定理得到了方程(1)可控的结果。显然，方程(1)是退化的,而在很多实际应用领域中，用中立型积分微分方程去刻画现实模型更为贴切,如:可以将具有有限波速的刚性热传导方程抽象为中立型Volterra型积分微分方程来研究[4]。虑到现实生活中一些系统的当前状态都充分依赖于过去的状态,Liu[2]研究了一类具无穷时滞的非线性中立型发展积分微分方程,利用Schaefer不动点定理、预解算子理论和粘贴技巧获得了系统可控性的充分条件。

时滞依赖于状态的微分方程可以用来建立电动力学中的粒子运动数学模型[5],在近些年被广泛应用于物理、生态学、神经网络等领域[6-7]。此外,Ito型随机微分方程(SDE)能够更为贴切地描述现实世界中的随机现象[8]。因此,考虑脉冲和随机白噪声的综合影响,研究时滞依赖于状态的脉冲中立型随机积分微分方程更具现实意义。Lin等[9]和Li等[10]分别利用解析预解算子理论和不动点定理获得了脉冲中立型随机积分微分方程温和解的存在性和渐近可控性结果,Ma等[11]利用分数阶算子理论、算子半群方法和不动点定理研究了一类分数阶布朗运动驱动的脉冲中立型随机积分微分方程的指数稳定性，但他们并没有考虑时滞依赖于状态的情形，而且文献[9-11]中所用到的解析预解算子理论和分数阶算子理论也不能用来处理如方程(1)中带有算子族A(t)的随机发展积分微分方程的相关问题。

受文献[1-2]启发,本文研究如下带有无穷时滞且时滞依赖于状态的脉冲中立型随机发展积分微分方程温和解的存在性。

1 预备知识

L(K;H)表示由K到H的有界线性算子的全体，赋以范数||∙||。设对称的非负定迹族算子Q:K→K，满足是Q的非负特征值序列。记L(K,H)为L(K;H)的完备化空间，其范数定义为Q。将强可测且均方可积的H—值随机变量的集合记为L2(Ω,H)，范数定义为。记C(J,L2(Ω,H))为所有将J映到L2(Ω,H)，且满足 supt∈JE||x(t)||2＜∞的连续映射组成的Banach 空间，其子集定义为是L0可测的}。关于Q-Wiener过程更为详细的介绍参见文献[12]。

如果函数x:[α,β]→H是分段连续且在区间(α,β]上左连续，则称x在区间[α,β]上是标准的分段连续函数。将区间[α,β]映到H的标准分段连续且Ft—适应的可测过程的集合记为P([α,β],H)。用P来表示所有Ft—适应可测的H—值随机过程{x(t):t∈[0,T]}的全体，其中x在t≠tk处连续，且存在，k=1,2,…,n，则(P,||·||P)是一个Banach空间，其上范数为

将(-∞,0]映到H的F0—可测函数的集合定义为相空间ℬ并赋以半模||·||ℬ，则ℬ满足以下公理性假设[13]：

Hg1：若x:(-∞,η+T]→H，T＞0 使得xη∈ℬ 和x|[η,η+T]∈P([η,η+T],H)，则对任意的t∈[η,η+T)，下列条件成立：

1)xt∈ℬ,

2)E||x(t)||≤γ||xt||,

其中γ＞0 是一个常数，M(·),N(·):[0,+∞)→[0,+∞)，M(·)是连续的，N(·)是局部有界的，γ，M(·)，N(·)与x(·)无关。对于 Hg1中的x(·)，xt在 [η,η+T]上是 ℬ —值连续函数。

Hg2：空间ℬ是完备的。

引理1[9]设x:(-∞,T]→H是一个Ft适应的可测过程，使得F0—适应过程且x|J∈P(J,H)，则有

对于∀t∈[0,T]，方程(2)中的A(t)是闭线性算子族。设：D(A)为其定义域，为稠密的且与t无关；0≤s≤t≤T，B(t,s)也是闭线性算子族；Y是D(A)的子集，赋以图范数||y||Y=:||A(0)y||+||y||，∀y∈Y，则Y是一个Banach空间。将Y映到H的有界线性算子全体记为B(Y,H)，用B(H)表示H中的有界线性算子。此外，假设A(t)和B(t,s)分别在0≤t≤T和0≤s≤t≤T上连续。

定义1[1,14]方程(2)的预解算子R(t,s)∈B(H)，0≤s≤t≤T具有如下性质：

1)R(t,s)关于s和t是强连续的，R(s,s)=I，0≤s≤T，且存在常数M和β使得||R(t,s)||≤Meβ(t-s)；

2)R(t,s)Y⊂Y，R(t,s)在Y上关于s和t是强连续的；

3)对于任意的x∈D(A)，R(t,s)x关于s和t强连续可微，且有

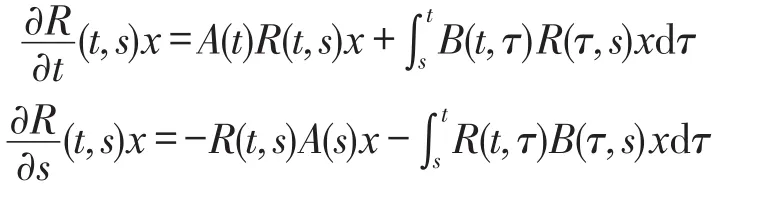
2 主要结论

定义2如果x0=φ∈ℬ，xρ(s,xs)∈ℬ 满足，x|J∈P，s∈J。当s∈[0,T]时，函数A(s)R(t,s)h(s,xs)可积，且如下条件成立：

1){xt:t∈J}是 ℬ —值的，且x(·)在(tk,tk+1]，k=1,2,…,n上连续；

2) Δx(tk)=Ik(xtk)，k=1,2,…,n；

3)对于任意的t∈J}，x(t)满足

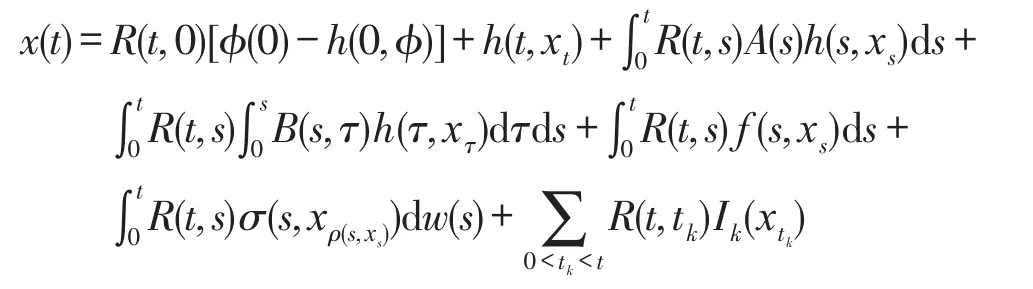
则称Ft适应的随机过程x:(-∞,T]→H是方程(2)的一个温和解。

假设ρ:J×ℬ→(-∞,T]是连续的且φ∈ℬ，并作如下假设：

(H1)令R(ρ-)={ρ(s,ψ)≤0,ρ(s,ψ):(s,ψ)∈J×ℬ}。 函数t→φt将集合R(ρ-)映到 ℬ，且存在连续有界函数Jφ:R(ρ-)→(0,∞)使得||φt||ℬ≤Jφ(t)||φ||ℬ，t∈R(ρ-)。

(H2)存在常数Mi＞0，i=1,2,3，使得||R(t,s)||2≤M1，||R(t,s)A(s)||2≤M2，||B(t,s)||2≤M3。

(H3)映射F:J×ℬ→H是连续的且存在常数MF＞0 和，对于任意的x,y∈ℬ，有。

(H4)映射f:J×ℬ→H是连续的且存在常数Mf＞0和，对于任意的x,y∈ℬ，有。

(H5)映射σ:J×ℬ→LQ(K,H)是连续的且存在常数Mσ＞0 和，对于任意的x,y∈ℬ，有。

(H6)映射Ik：ℬ→H是连续的且存在常数MIk＞0 和，k=1,2,…,n,对于任意的x,y∈ℬ，有。

由公理性假设Hg1及假设条件(H1)易得如下引理：

引理2设x：(-∞,T]→H，x0=φ且x|J∈P，则有

定理1假设条件(H1)-(H6)成立且。若

则方程(2)存在一个温和解。

证明令Y={x∈P:x(0)=φ(0)}为一个一致收敛拓扑空间。对于任意的正数r，记Br(0,Y)={x∈Y:E||x||2≤r}，则Br(0,Y)是Y中的一个有界闭凸子集。定义算子Φ:Y→Y如下：

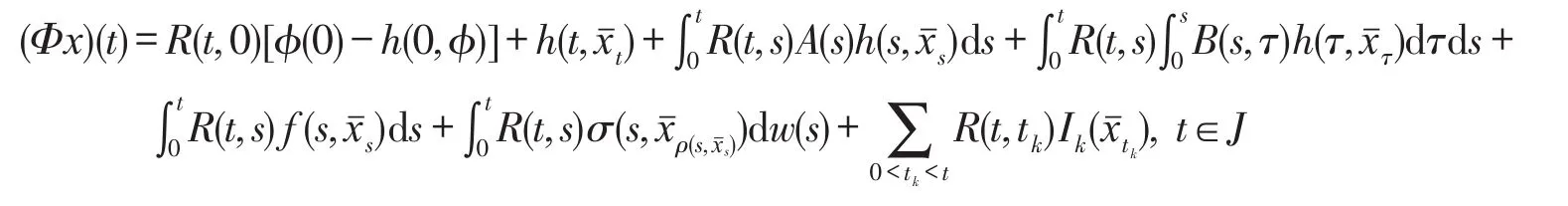
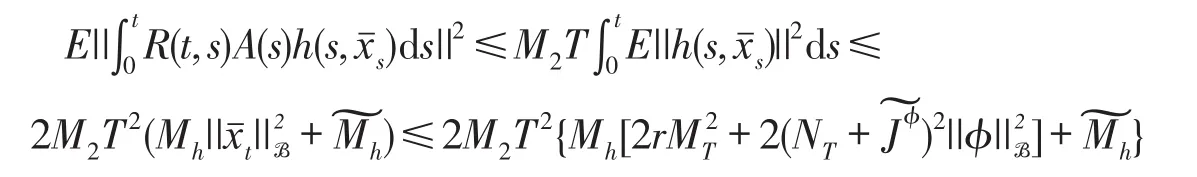
第一步：存在常数r＞0，使得Φ(Br(0,Y))⊆Br(0,Y)。

对于任意的r＞0，Br(0,Y)={x∈Y|E||x||2≤r}显然是P的一个有界闭凸子集。可断言存在正数r＞0使得Φ(Br(0,Y))⊆Br(0,Y)成立。假如断言不成立，则对∀r＞0，存在xr(tr)∈Br(0,Y)，但Φ(xr)∉Br(0,Y)，即存在tr∈J使得r＜E||(Φxr)(tr)||2。然而，由引理2，Ho¨lder不等式和其他假设条件可知

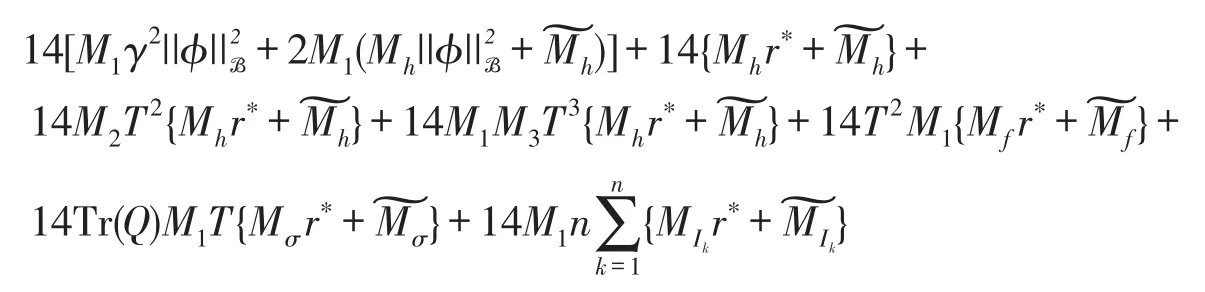
这与式(5)矛盾，故断言成立。

第二步：Φ是压缩的。取x,y∈Br(0,)，有

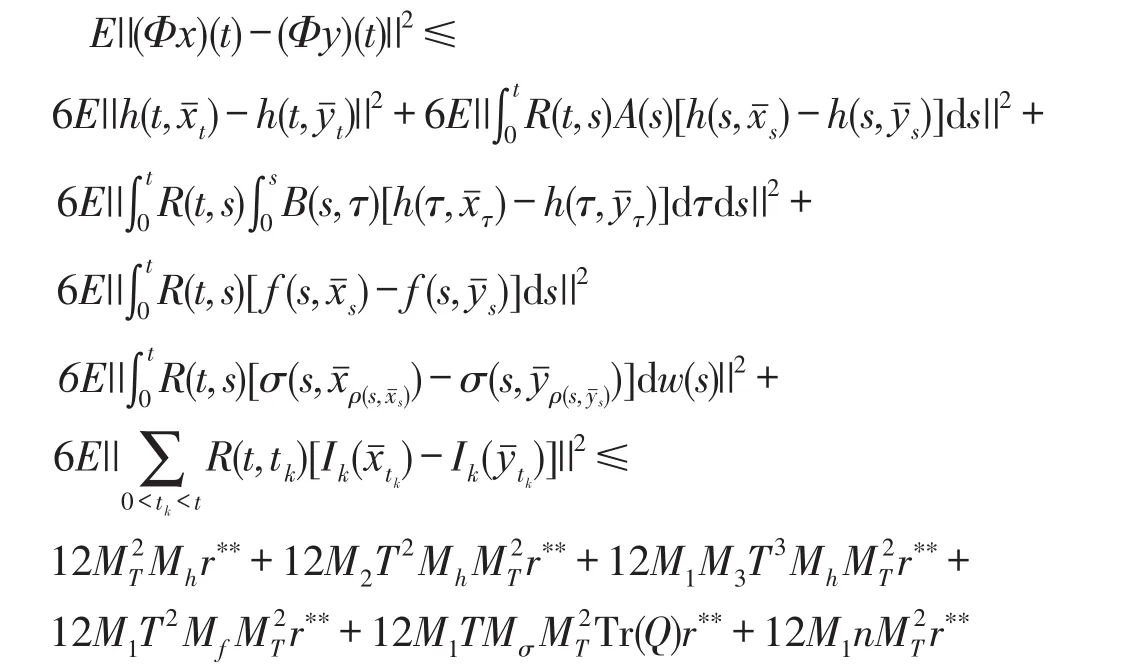
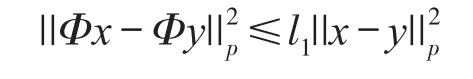
其中

由式(3)可知l1＜1，从而可证算子Φ是压缩的。利用Banach不动点定理知算子Φ在Br(0,Y)存在唯一的不动点，其实该不动点也就是方程(2)的一个温和解。

3 实例论证

考虑如下时滞依赖于状态的随机热传导方程：

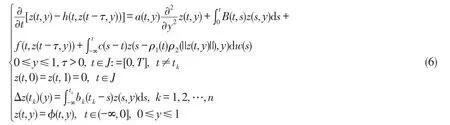
其中w(t)表示实可分的Hilbert空间H中的一个Wiener过程。设H=L2[0,1]，a(t,y)和B(t,s)是连续函数且存在正数M使得||B(t,s)||2≤M。

定义A(t):H→H为 (A(t)ω)(y)=a(t,y)ω″，其定义域为D(A)={ω∈H:ω,ω″绝对连续，ω″∈H,ω(0)=ω(1)=0}。R(t,s)为方程(6)的一个预解算子并满足||R(t,s)||2≤M1，||R(t,s)A(s)||2≤M2，其中M1和M2为两个正数。

这里取相空间 ℬ=P0×L2(g,H)，其验证见文献[13]。假设当t≤0 时，函数φ(t,·)∈ℬ 且φ(t,y)=φ(t)(y)，(t,y)∈(-∞,0]×[0,1]。定义映射h，f，ρ，σ，Ik如下：

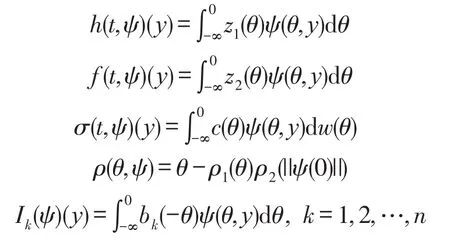
于是方程(6)能抽象为方程(2)。另外，作如下假设：

1)函数z1，z2在(-∞,0]上连续，且有

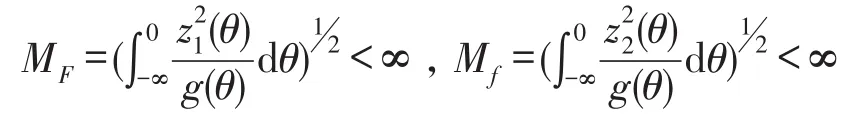
2)函数bk在R上连续且。

3)函数c:R→R，ρi:[0,∞)→[0,∞)(i=1,2)均连续，且有

在以上假设条件下，可得h，f，σ，Ik(k=1,2,…,n)均有界，即||h||2≤Mh，||f||2≤Mf，||σ||2≤Mσ，||Ik||2≤MIk,k=1,2,…,n。因此，由定理1可知方程(6)在J上存在一个温和解。