基于GA-BP神经网络的船用柴油机制造企业供应商评价

邓 浩，吴玉国，徐先进

(1.安徽工业大学管理科学与工程学院，安徽马鞍山243032；2.安庆中船柴油机有限公司，安徽安庆246003)

船用柴油机是船舶的核心设备，其制造业直接影响我国造船工业的发展。目前，我国船用柴油机制造企业在生产过程中所需要的配套部件有很大比重由合作供应商提供，因此，供应商评价结果的准确性对船用柴油机企业成本的控制及产品交付等各环节有着显著的影响[1]。在供应链管理的大趋势下，客观、准确的供应商评价能够帮助船用柴油机制造企业获得长期稳定的合作伙伴，给企业高效持续发展提供重要保障[2]。

国内外学者对供应商选择与评价做了大量的理论和实践研究。Dickson[3]于1966年最先对供应商评价进行了研究，提出质量、交货以及历史效益是供应商选择的三个关键性因素。此后，文献[4-7]从社会标准、低碳环保、服务以及创新等方面对供应商评价指标体系进行了丰富和发展。供应商评价为多属性决策问题，很多定性和定量的方法被应用于供应商的评价与选择，如层次分析法[8]、理想解法(TOPSIS)[9]、模糊综合评价法[10]、熵权法[11]以及灰色关联分析法[12]等。

目前，针对船用柴油机制造企业供应商评价问题的研究主要集中在供应商评价指标的筛选、评价指标权重的确定等方面。文献[13-14]分别对船用柴油机造企业供应商的分类分级动态管理以及基于供应商现状的评价指标体系构建两个方面进行了研究。总的来说，供应商评价指标体系的构建多数仍停留在价格、质量等传统指标上，评价方法仍以专家打分以及层次分析法等定性分析比重很大的方法为主，难以对供应商做出全面的评价。

在进行供应商评价时，指标之间的关系十分复杂，往往呈现出非线性的特点。而诸如层次分析法等传统评价方法通常需要人为计算权值，受主观影响较大，具有较强的不确定性。GA-BP神经网络模型能够进行自组织、自学习，有很强的泛化能力，输入供应商数据进行训练后，可以对专家经验进行充分的学习，找出评价指标数据和评价结果间的内在联系，以对供应商进行更为科学、客观的评价。

鉴于此，本文运用因子分析法对供应商初始评价指标进行筛选，基于遗传算法优化的BP神经网络模型，构建针对船用柴油机制造企业的供应商评价指标体系。

1 评价指标体系的构建

1.1 供应商评价指标的初选

从企业供应商管理的实际情况出发，结合对国内外供应商评价指标研究成果的分析，对常年从事船用柴油机制造行业供应商管理的专家进行深入访谈以及广泛调查后，确立评价指标初选集如表1所示。

表1 船用柴油机企业供应商评价指标初选集Tab.1 Supplier evaluation index set of marine diesel engine manufacturers

1.2 评价指标重要度问卷调查

1.2.1 调查目的

对表1中的评价指标在船用柴油机制造企业供应商评价中的重要程度进行问卷调查，并以问卷数据为基础进行因子分析。根据因子分析结果，将方差贡献率作为权重，对指标因子载荷值的绝对值进行加权计算，将计算结果的最大值作为该指标解释初始评价指标集信息含量的比率，并以此为依据对初始指标集中的指标进行筛选，最终构建出适用于船用柴油机制造企业供应商评价的指标体系。

1.2.2 调查对象与样本特征

本次问卷调查的对象主要分为船用柴油机制造企业供应商管理从业人员和从事供应商管理研究的专家学者两部分。从调查对象的从业经验来看，被调查者常年从事与供应商管理相关的工作，有着丰富的从业经验，其中，从业经验为5至10年的占比为51.7%，11至20年的占比为20.8%，20年以上的占比为5.8%。从调查对象的从业背景来看，企业相关从业人员占比为65%，高校及研究机构相关专家学者占比为35%。

1.2.3 调查问卷的设计

调查问卷主要包括指导语、被调查者相关信息以及问题描述和选项三部分内容。问卷中的问题为封闭式，按照表1中的22条评价指标设计。指标重要度分别用1到7标记，对应从非常不重要到非常重要七个等级，具体标准如表2所示。

表2 调查问卷指标重要度标准Tab.2 Significance standard of questionnaire index

1.2.4 调查问卷的发放与回收

本文进行调查问卷发放与回收的渠道主要有电子邮件、人员访谈等方式，发放问卷总数为120份，收回112份，问卷回收比率为94.17%，去除无效问卷9份，有效率为85.83%。

1.3 问卷数据因子分析

本文对问卷数据进行因子分析的目的是基于指标主要信息含量对评价指标进行筛选。

采用Bartlett球度检验法和KMO检验法对问卷进行结构效度检验，结果如表3所示。由表3可知：KMO值为0.803，大于0.6，显著性概率为0.000，小于0.005，问卷数据适合进行因子分析。

以原有变量的相关系数矩阵为依据，采用主成分分析法[15]，得到主成分因子特征值和方差贡献率的统计情况，如表4所示。

表3 KMO和Bartlett检验结果Tab.3 Test results of KMO and Bartlett

表4 主成分因子特征值和方差贡献率的统计情况Tab.4 Statistics of characteristic value and variance contribution rate of principal component factor

由表4可知，前6个因子解释原22个指标变量的信息比例可达85.403%。因此，选取前6个因子作为公共因子，记为F1～F6。

运用方差最大法对因子载荷矩阵作正交旋转，得到旋转因子载荷矩阵，结果如表5所示。

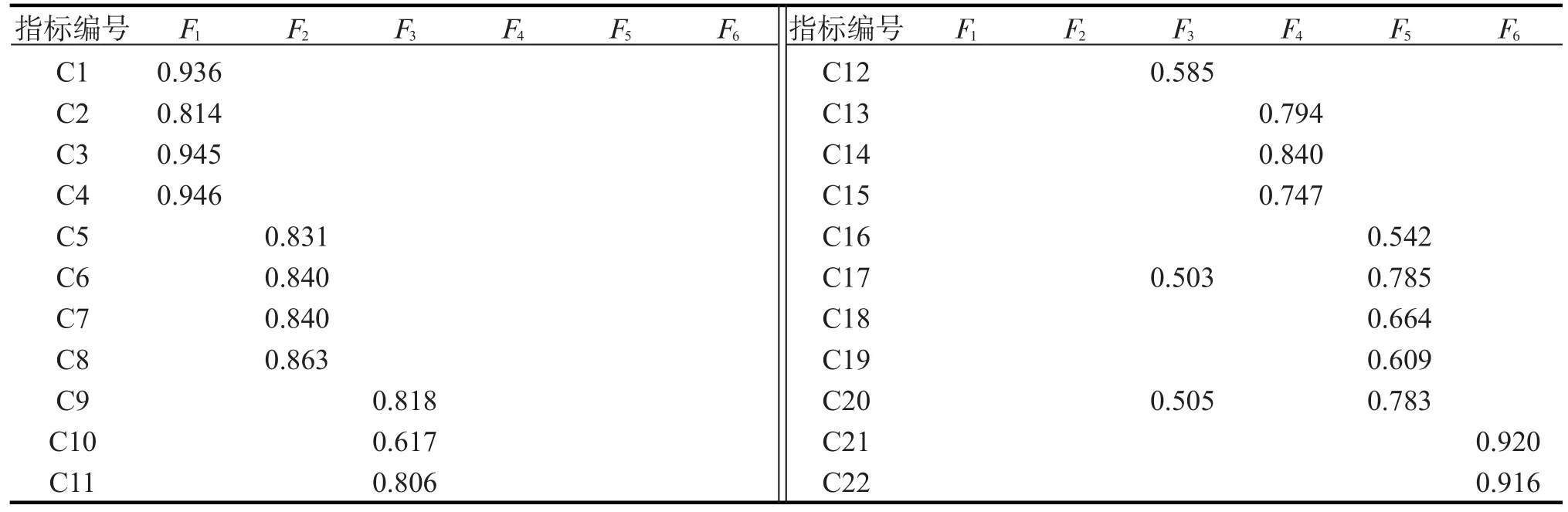
表5 旋转因子载荷矩阵Tab.5 Loading matrix of rotation factor

从表5中可以看出，因子分布相对合理，虽然存在双负荷现象，但是数量较少。因此，可以视为正交旋转使用合理，不需要再使用斜交旋转。

采用Alpha Cronbach α模型法[16]分析问卷信度，结果如表6所示。

表6 问卷信度检验结果Tab.6_ Results of questionnaire reliability test

由表6可知，问卷各公因子以及问卷总体的信度相关系数α都大于0.80，表明问卷有良好的稳定性和一致性，结果具有很高的信度水平。

1.4 初始评价指标筛选

在表5所示的因子载荷矩阵中，因子Fj对应原始指标Ci的因子载荷值(记为αij)表示的是两者间的相关性，进行正交旋转后，一个原始指标仅和一个因子有非常高的相关性，所以一个因子载荷就可以体现一个原始指标对因子的解释程度。因此，本文将因子Fj的方差贡献率βj作为权重，对指标Ci对应因子载荷αij的绝对值进行加权计算，计算结果的最大值反映该指标包含原始指标集信息量的多少[17]。

1)载荷因子的加权计算

其中：βj为正交旋转后因子Fj的方差贡献率；αij为因子Fj下指标Ci的因子载荷值。ηij为加权因子载荷，表示指标Ci在公因子Fj下解释原始指标集信息量的比例(i=1,2,…,n，n为初始指标个数；j=1,2,…,k，k为保留公因子的个数)。

2)指标Ci包含原始指标集信息量的计算

其中Qi表示指标Ci解释原始指标集信息比率的主要部分，称为指标Ci的信息含量。

3)信息含量Qi降序排列结构的构建

4)前m个指标信息含量占比Pm的计算

其中Qm表示前m个指标累计解释信息量的比率。

5)以信息含量比率Pm为依据的指标筛选

选取包含信息量最大的前m个指标，其中P0为保留指标信息包含量阈值，文中P0为80%。

根据以上步骤，结合因子分析的内容，对评价指标进行筛选，结果如表7所示。

由表7中的指标筛选情况可知，P15=76.9%＜80%＜P16=80.7%，因此保留信息含量最大的前16个指标，将剩余的信息含量小的指标予以剔除。

根据表7中指标筛选的结果，结合对相关专家的咨询，构建供应商指标体系如图1所示。

2 基于GA-BP神经网络的船用柴油机制造企业供应商评价模型

2.1 模型分析

运用因子分析法对初始指标集进行筛选后，构建了由6个一级指标和16个二级指标组成的供应商评价指标体系(图1)，指标之间呈现出非线性关系，因此对评价模型的非线性映射能力以及评价全面性的控制能力有着较高的要求。BP神经网络模型具有较强的非线性逼近能力，可以对样本数据进行大规模的并行处理，其误差反馈机制能够不断根据误差反向修改初始权值和阈值，提升模型运算精度，实现评价指标数据和评价结果间的非线性映射，模拟专家对供应商做出评价。但是BP神经网络有解集易陷入局部最优以及不易收敛等不足。鉴于此，本文采用遗传算法对BP神经网络进行优化，将遗传算法得到的最优解作为BP神经网络的初始权值和阈值，使模型在极小的调整下就可收敛，既避免了模型陷入局部最优，又提升了模型的运算效率。

表7 供应商评价指标筛选Tab.7 Selection of supplier evaluation index

图1 船用柴油机制造企业供应商评价指标体系Fig.1 Supplier Evaluation Index system of marine diesel engine manufacturers

2.2 GA-BP神经网络模型的设计

构建的GA-BP神经网络模型如图2所示。

2.3 评价模型的实施

2.3.1 供应商数据的搜集与处理

以某船用柴油机制造厂家ZC公司为对象，对该公司2017年100家供应商在图1中16个二级指标上的数据进行搜集。在MATLAB2016A中运用mapminmax函数对数据进行归一化处理。从该行业以及公司内部选取6位参与供应商管理工作的专家组建评审小组，分别对100家供应商的综合情况进行打分，求取6位专家打+分平均值作为该供应商的综合评价值并用作GA-BP神经网络训练的期望输出值，最终得到100个供应商样本数据。专家评分标准如表8所示。

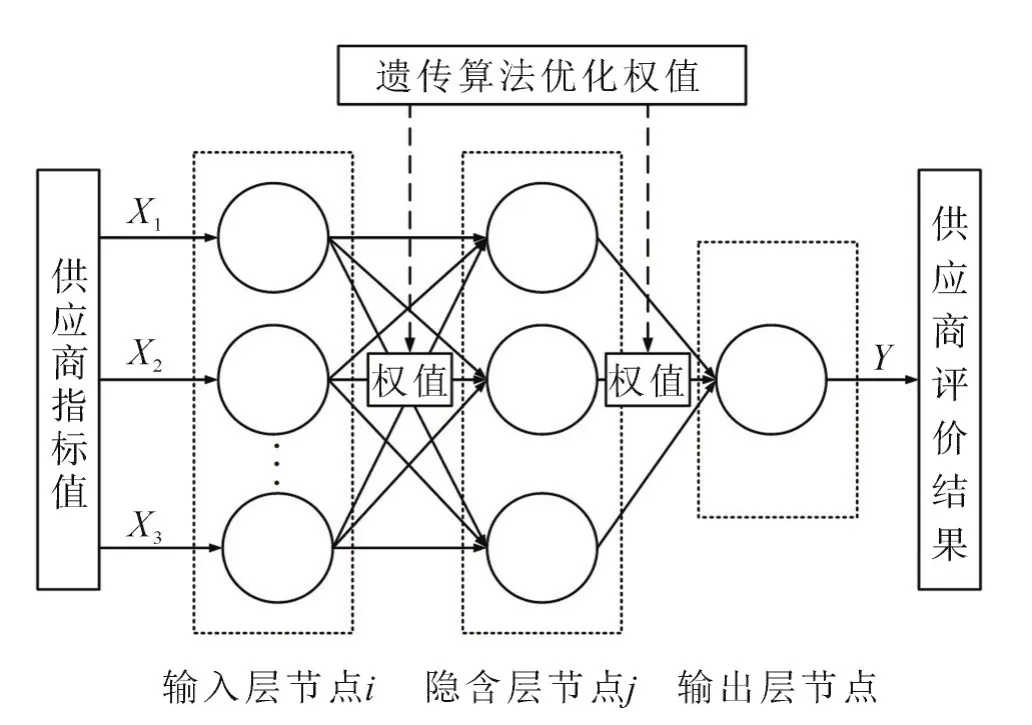
图2 GA-BP神经网络模型Fig.2 GA-BPneural network model

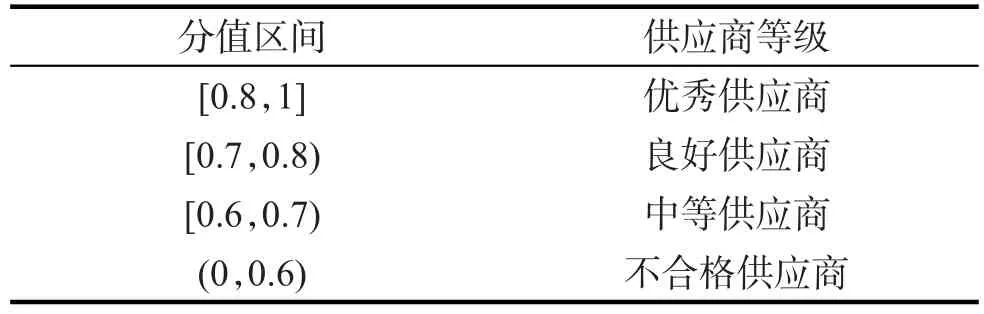
表8 供应商评分标准Tab.8_ Supplier scoring criteria

2.3.2 模型参数设定

1)BP神经网络参数设定

文中将BP神经网络结构设定为包括输入层、输出层和一个隐含层的三层结构。输入层神经元节点数等于输入数据的维度，二级评价指标为16个，因此该层神经元节点数为16。输出层为最终评价结果，神经元节点数为1。隐含层节点数采用以下经验公式估计[18]。

其中：c为隐含层节点数；m为输入层节点数；n为输出层节点数；a为[0,10]之间的常数。

根据式(6)，结合大量实验测试，文中确定模型的隐含层节点数为5。

经过多次实验调整，最终设定学习率为0.01，期望误差为1×10-5，最大迭代次数为1 000次。隐含层传递函数选用tansig函数，输出层传递函数选用purelin线性函数。训练采用Levenberg-Marquardt算法，该种算法具有快速收敛、运算精度高等特点[19]。

2)遗传算法参数设定

在保证算法整体性能的前提下，文中设置种群规模为40，编码方式为二进制编码，变量二进制位数为10，选择算子为随机遍历抽样，交叉方式为单点交叉，交叉概率设定为0.9。变异算子采用基本位的变异方式，变异概率为0.01。代沟为0.95。最大遗传代数为100代。

将预训练的输出值与期望值误差矩阵的范数作为目标函数的输出，根据目标函数的输出，运用基于排序的适应度分配函数RANKING函数对个体适应度值进行分配，其适应度分配机制为：对目标值进行排序，最大值分配最小的适应度值，最小值分配最大的适应度值。

2.3.3 模型的训练与仿真

1)模型的训练

模型参数设定完成后，本文运用MATLAB2016A对模型进行编程，将ZC公司100家供应商前90家样本数据作为训练样本。

模型输出值与目标值之间误差范数的变化如图3所示。经过100次迭代之后，误差值逐渐趋于平稳，初始权值和阈值不断得到优化，并最终趋于稳定。

图3 误差变化趋势图Fig.3 Chart of error trend

将遗传算法优化后的初始权值和阈值输入BP神经网络模型进行训练，训练结果如图4所示。从图4的训练结果可以看出，经过6次误差调整后趋于收敛，全局误差为3.5×10-6，低于模型要求的1×10-5，模型训练结果符合预设要求。

2)模型的仿真测试

把ZC公司剩余的10家供应商数据输入训练后的BP神经网络模型，使用sim函数进行仿真测试。输出值与期望值的拟合情况如图5所示。输出值与期望值的误差如表9所示。

表9 供应商评价模型仿真结果误差Tab.9 Error of simulation results of supplier evaluation model

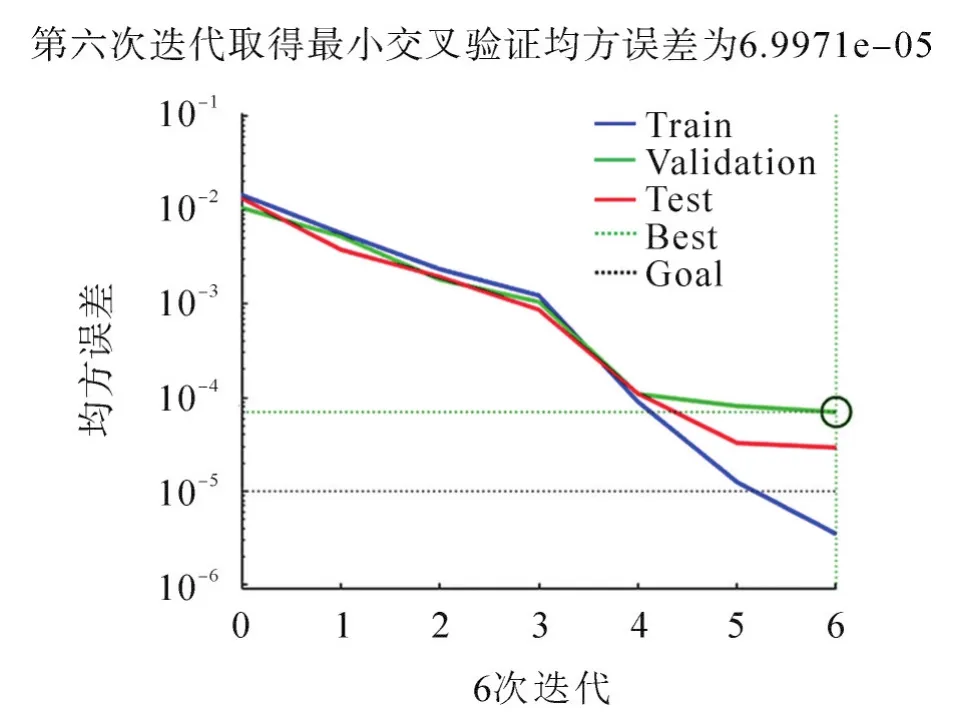
图4 GA-BP网络训练结果Fig.4 Training knot of GA-BPnetwork

图5 仿真输出与期望输出结果对比Fig.5 Comparison of simulation output with expected output results

由图5数据拟合状态及表9中的误差分析可知，ZC公司10家供应商进行仿真测试的误差低于1%，输出值与期望值基本吻合，表明构建的模型具有良好的学习、记忆能力，可以很好地应用于ZC公司的供应商评价。

2.3.4 模型的比较分析

为了验证遗传算法对BP神经网络的优化效果，文中将GA-BP神经网络模型与未使用遗传算法优化的BP神经网络模型从收敛性、精确性及稳定性三个方面进行对比分析。

1)收敛性

图6为BP神经网络训练结果。从图6可知，BP神经网络的收敛步数为9，最大误差为9.19×10-6，GA-BP神经网的收敛步数及最大误差都小于该模型，所以GA-BP神经网络收敛性要优于该模型。

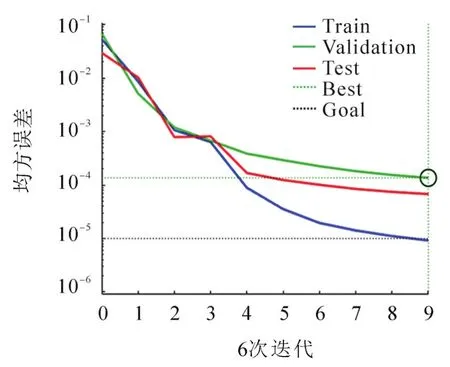
图6 BP网络训练结果Fig.6 Results of BPnetwork training

2)精确性及稳定性

对BP神经网络模型进行仿真测试，与GA-BP神经网络模型的结果对比，如表10所示。

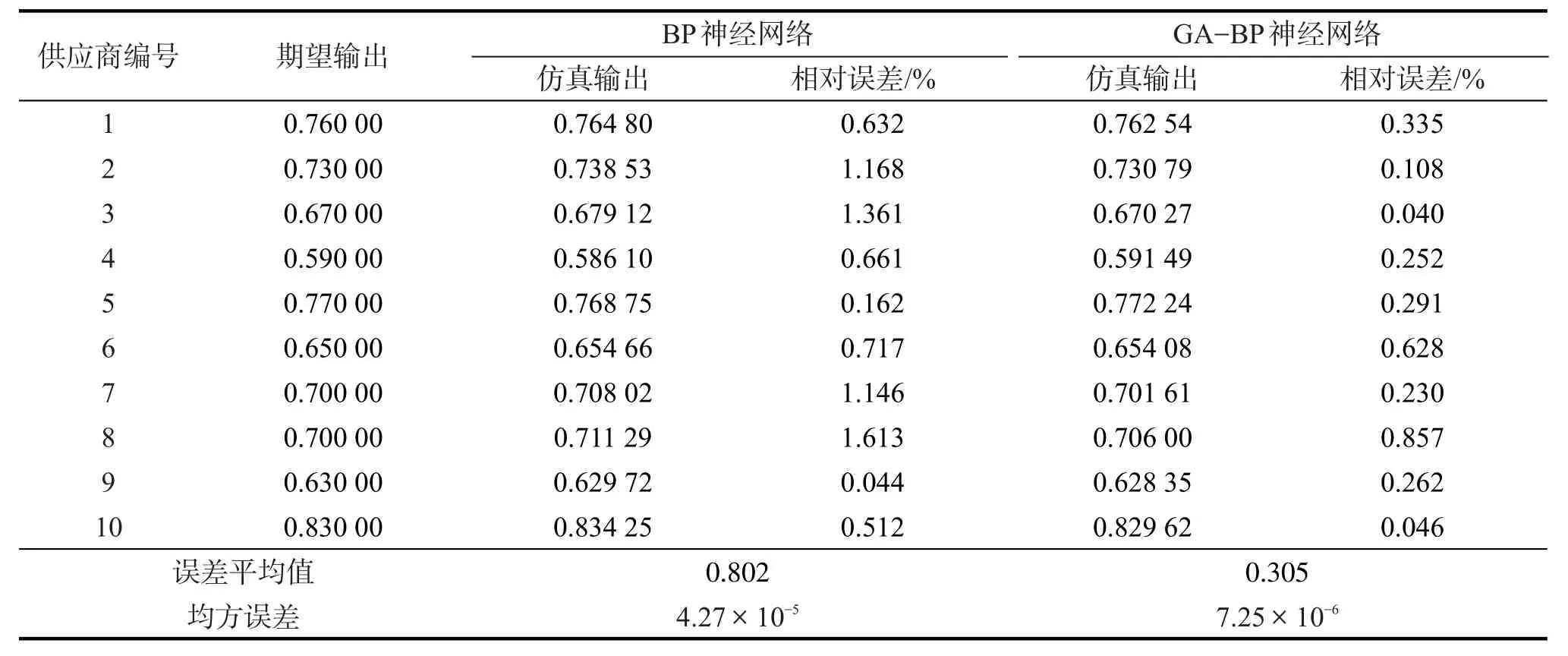
表10 测试样本数据仿真结果Tab.10 Simulation results of test sam ple data

由表10可知，GA-BP神经网络模型仿真测试的相对误差及误差平均值都远小于BP神经网络,运算精度更高，均方误差也远远小于BP神经网络，相对误差稳定在1%以内，上下波动很小，具有很好的稳定性。而BP神经网络模型相对误差有着很大的波动，其中一个测试点的相对误差达到了1.6%以上，极可能陷入了局部极小值。

通过上述对比分析来看，GA-BP神经网络模型对专家经验的学习更为充分，综合性能更为优越，能够更加准确地对ZC公司供应商进行有效评价。

3 结 论

围绕船用柴油机制造企业的实际情况，运用调查问卷和因子分析法构建了针对该行业的供应商评价指标体系。将遗传算法和BP神经网络结合，建立了基于GA-BP神经网络的供应商评价模型。运用船用柴油机制造商ZC公司的供应商数据对模型进行实证研究，确立了模型的可行性和实用性。结果表明，该模型同时具有神经网络模型自适应、自学习以及遗传算法求取全局最优解的能力，能够对专家的经验和知识进行充分的学习，对供应商进行准确的定量评价，对船用柴油机制造企业的供应商评价具有一定的实践应用价值。