动态学习机制的双种群蚁群算法*

袁汪凰，游晓明，刘 升

1.上海工程技术大学 电子电气工程学院，上海 201600

2.上海工程技术大学 管理学院，上海 201600

1 引言

蚁群优化算法自1992年由意大利学者Dorigo提出来较优地解决了组合优化问题，引起了专家学者的重视。该算法模拟自然界蚂蚁的觅食行为，即蚂蚁从巢穴出发利用前一批次的蚂蚁释放的信息素选取到达目标点的最优路径。过去一些年中，专家学者在蚂蚁系统的基础上对蚁群算法进行了一系列的改进，从而能够更好地应用到组合优化的问题中[1-4]。在这些改进中主要有三个方向：其一是单种群蚁群算法内部机制的改进[5-7]；其二是蚁群算法与其他算法的结合[8-9]；其三是多种群机制的改进[10-14]。在蚁群算法研究过程中，一个很重要的测试算法性能的基准即是旅行商问题。在TSP（traveling salesman problem）中，旅行商从所有城市列表中选择任一城市作为出发点，不重复地访问每个城市，最后回到出发点。

自然界中的生存准则：“物竞天择，适者生存”。生物通过这种方式衍生下去。蚂蚁则是根据生存环境形成了一种具有分工性质的群体合作方式，从而提高群体的生存技能。有人根据蚂蚁的自然合作行为，提出了多种群蚁群算法。Gambardella等[10]在解决带时间窗的车辆路径问题（vehicle routing problem with time windows，VRPTW）上，提出了MACS-VRPTW（multiple ant colony system for vehicle routing problems with time windows），该算法定义了两个蚁群系统（ant colony system，ACS），其中种群ACS-VEI旨在减少车辆的使用数量，ACS-TIME旨在优化ACS-VEI找到的可行解的时间，两个种群通过信息素的更新交换信息，通过实验得出该算法从解的质量和求解时间上来看，比单种群更具有优势。Sim等[11]针对大多数蚁群算法存在停滞问题提出一种新的多种群算法MACO（multiple ant-colony optimization），采用多个蚁群寻找最优路径，增加了MACO的探索更优路径的能力，一定程度上提高了适应性和减少停滞的可能性。可见，为了更好地探索和开发空间，采用几个蚁群并行地处理优化问题，可以在一定程度上提高多样性，减少算法陷入停滞的可能性。Mavrovouniotis和Yang等在MMAS（max-min ant system）的基础上提出多蚁群算法并用于解决动态TSP问题（dynamic travelling salesman problem，DTSP）[12]。每个种群（拥有各自的信息素表）并行运行，当出现新的全局最优解，将其传递给所有种群，并且通过实验验证了多种群蚁群算法在一定程度上提高了多样性，且比单种群蚁群算法具有更优的性能。同时根据种群间参数的不同提出了同构与异构的概念，并通过实验表明异构的性能优于同构。张鹏等提出了基于相识度的自适应异类多种群蚁群算法[13]，根据各个子种群间的相识度，自适应选择需要进行通讯的子群，并根据相似度系数来决定交换各自的最优解和信息素的时间间隔，实现多种群的合作与竞争，缓解蚁群算法容易早熟、停滞与收敛速度的矛盾。邓可等提出了基于信息熵的异类多种群蚁群算法[14]，算法引入信息熵来表示蚂蚁种群的进化程度，通过信息熵决定多个异类子群体间选择交流的对象以及交流策略，从而取得各自种群的多样性与收敛速度的平衡。上述专家学者采用固定模式的种群交流策略，即种群在运行期间交换信息，在种群合作上具有局限性，导致模型的自适应性能有待提高，对于解决中大规模TSP问题效果并不理想。Lalbakhsh等对蚂蚁算法（ant colony optimization，ACO）的奖励不作为模型[15]，即只有最优的蚂蚁被强化信息素，非最优蚂蚁的信息素保持恒定，对此进行了改进，提出基于奖惩强化学习的蚁群网络路由算法，在其蚁群网络路由算法中引入惩罚因子，利用发生检测对当前状态进行检测，识别行为的最优性和非最优性。最优性采用奖励增强，对于非最优行为利用惩罚因子进行惩罚策略。在NSFnet拓扑结构上进行了仿真，改进算法的瞬时分组延迟和吞吐量皆优于标准的蚂蚁网络。可见，该策略增加了算法的勘探能力，提高了算法的性能，但他们对其中的动态学习机制并未进行进一步的探讨。

本文主要研究种群交流后的学习机制，从而对种群间交流产生一个及时评价和反馈。借鉴Lalbakhsh奖惩强化学习的思想，提出了动态学习机制的双种群蚁群算法（dual population ant colony algorithm based on dynamic learning，DACO-DL）。该算法的两个种群分别采用SA-MMAS（adaptive simulated annealing ant colony algorithm based on max-min ant system）与MMAS两种算法。这两种算法并行搜索一定代数后进行信息素的学习交流，对交流后两个种群搜索出的最优路径作一个即时的评价和反馈，若两个种群交流后任意种群的最优路径与期望路径间隔逐渐缩短，且满足奖惩模型，则奖励该种群，奖励程度根据奖惩模型所属的权重因子进行动态的奖励，提高了算法的收敛速度；如果两个种群在交流后，两个种群的评价算子不属于权重因子范围内，则根据奖惩模型动态地惩罚该种群，增加了蚂蚁群体的勘探能力。种群间交流后的奖惩模型，达到了平衡各蚂蚁群体的多样性与收敛速度的效果。通过对学习机制的探讨完善种群合作，提高算法的自适应性能，对于解决中大规模问题有较好的效果。

2 相关工作

2.1 蚁群算法ACO在TSP上的应用

自然界中的蚂蚁没有发育完全的视觉系统，但是却能够以最短的路径有秩序地寻找到食物。为此，1991年Dorigo根据自然界中蚂蚁的行为提出了AS（ant system），用于求解TSP问题，这是ACO算法的起源。首先每个蚂蚁被随机地分配到城市中，然后根据状态转移概率寻找下一个要到达的城市。

其中，τij是连接着城市i与城市j边缘的信息素强度值；allowedk∈{n-tabuk}表示第k个蚂蚁尚未访问的城市集合；tabuk记录了蚂蚁k当前已走过的城市，其根据蚂蚁周游城市进行动态的变化；ηij(t)是启发式函数，是城市i与城市j之间的距离；参数α决定了信息素信息的重要性；参数β决定了启发式信息的重要性，其值越大，启发式在状态转移概率中的作用越大。当迭代结束后，更新所有路径上的信息素，规则如下：

式中，ρ(0≤ρ≤1)为信息素挥发系数；Δτij(t)为本次循环后在城市i和城市j边缘路径上信息素的增量；Δτkij(t)为第k只蚂蚁在本次循环后残留在路径i到j的信息素，一般采用：

其中，Q表示信息素强度；Lk为第k只蚂蚁在当前循环中所走路径长度。

2.2 最大最小蚁群算法

MMAS算法的经典改进之处在于给定信息素一个限制域，避免因次优路径上信息素不断累积而造成的算法停滞。该算法由Stuetzle和Hoos于1997年提出，并在解决TSP问题和QAP（quadratic assignment problem）问题上取得了较好的效果。对于MMAS算法，做了较多的改进：

在信息素更新方式上，只允许迭代最优蚂蚁或者至今最优蚂蚁进行信息素的释放，迭代最优蚂蚁更新信息素，算法的收敛性性能较好，但是会使得多样性不足，至今最优蚂蚁更新信息素，算法的探索能力强，但是搜索效率不高，实际上这两种方式交替使用，从而使算法达到一个较好的性能水平。

各个路径上的信息素浓度限制在一定的范围[τmin,τmax]，从而避免某些路径上的信息素增加过快，从而导致算法的早熟。

初始信息素设置为信息素限制域的最大值，从而扩大了搜索范围，提高算法的多样性。

当算法进入停滞时将所有路径上的信息素重新初始化，从而在后续的迭代周期内继续进行搜索，增加算法的全局搜索能力。

3 动态学习机制的双种群蚁群算法

双种群交流中种群的选取有两种类型：同构和异构。研究文献[12]表明异构优于同构，故本文采用异构种群即MMAS和SA-MMAS[16]。SA-MMAS算法的种群前期由于模拟退火的扰动，使得多样性好，中期通过降温，提高了算法的收敛速度，后期为了避免陷入局部最优加入回火机制，跳出局部最优，提高了算法多样性。其信息素是自适应更新，相较原始的MMAS算法，两者信息素更新方式不一致，从而形成异构机制。此外本文通过对两个种群不同期段的设置令SA-MMAS侧重于多样性，MMAS侧重于收敛速度，两者形成互补，有利于算法性能的提高。

3.1 SA-MMAS

针对蚁群算法容易出现早熟和陷入局部最优的情况，而模拟退火算法具有概率突跳的能力，能有效地避免在搜索过程中陷入局部最优，笔者曾提出SAMMAS算法。m只蚂蚁一轮搜索后得到初始解S1,计算出初始解的当前最优路线距离为R1,在初始解的基础上随机扰动产生一组新解S2,由新解计算 出的最优路线距离为R2,从而根据式（5）计算目标函数值：

然后根据Metropolis法则判断是否接受新解，即当ΔS＜0时，接受新解作为当前解，否则根据式（6）判断是否接受新解。

式中，T是系统当前温度。

在（0,1）之间随机产生一个随机数ξ。如果P＞ξ，则接受新解作为当前解，否则保留原路线。

在完成一轮搜索后，进行信息素更新，更新公式如式（2），其中ρ为式（7）：

信息素更新后，按照式（8）进行降温：

式中，q是降温系数。

模拟退火的过程是随着系统温度T的下降而逐渐向最低能量态收敛，当系统温度高时，将会以高的概率接受次优解，使得算法具有较好的全局搜索能力。随着系统温度的下降，接受次优解的概率逐渐降低，从而加快了算法的收敛速度，而q的取值也影响着算法收敛速度的快慢，q取值越小，则系统温度下降得越快，也加快了算法的收敛速度。然而运行后期随着T→0，算法陷入局部次优点的概率逐渐增大，退化成局部搜索算法，这不是所希望的，因此在该算法中加入回火退火算子，设置回火温度范围为[Tmin,Tmax]，即降温后重新对T值进行提升（加温），当T＜Tmin，将系统温度升高到Tmax，重新进行退火过程，提升了算法接受次优解的概率，从而跳出局部最优，加大全局搜索能力。由于回火会造成重复性搜索，因此回火的次数不宜过多，正常在10次以内。

3.2 学习机制

基于动态学习机制的双种群蚁群算法采用了MMAS和SA-MMAS两个种群并行搜索，两个种群并行搜索一定的代数后，通过交换各自的信息进行交流合作，从而向另外一个种群学习。交互后，借鉴Q-learning中“奖励先进，惩罚后进”的思想。学习的目标则是：针对TSP问题，利用蚁群算法寻找出一条最短的哈密顿回路，因此如果当前迭代最优路径与期望路径的差距逐渐缩小，则动态地奖励该种群，否则惩罚该种群，从而对两个种群之间的学习状态产生一种及时反馈，使得优者更优，强者更强，如图1。利用两个种群间的相互合作交流，在整个周期平衡了算法的多样性和收敛性。

3.2.1 交流机制

Fig.1 Learning mechanisms图1 学习机制

蚁群之间通过交流学习，从而使得每个种群皆能找到一个更优的解。种群之间的交流涉及到何时进行交流，种群间如何选择（哪些种群给予信息，哪些种群接受信息），交流什么样的信息[17]，对于双种群则只需要考虑每隔多长时间进行交流以及交流怎样的信息。根据不同的城市规模设定不同的交流次数。总的迭代次数为NC，在算法运行进程中两个种群随机交流[1%,2%]×NC次，迭代次数越大，两个种群的交流次数越多。可见，在大规模城市中迭代次数多，交流次数也相应得多；相反小规模城市的迭代次数少，两个种群的交流次数也少。通过该种交流方式，使得算法对于不同规模的城市产生与之匹配的适应度。

种群之间主要从解和信息素矩阵两方面进行交流[18]，根据式（9）进行交流：

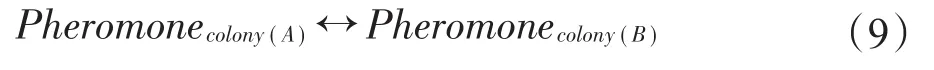
即将种群A和种群B的信息素进行交换，然而信息素的限制域被当前最优路径所影响，由于每个子种群在交流之前的当前最优路径不一致，则在交流后容易使得信息素的值超出限制域，因此在两个种群交流后，对交流后的信息素矩阵采用信息素强制限制的策略，使得交流后的信息素保持在限制域内。

信息素交流若过于频繁，会减少算法的多样性，延长搜索路径的时间；如果交流时间间隔太长，将影响种群学习机制的效率。种群间根据城市规模自适应交流，既不破坏各种群的搜索性能，又能发挥出双种群学习机制的性能，从而平衡整个算法的收敛速度与多样性。

3.2.2 动态学习的奖惩模型

种群A和种群B学习交流之后，采取一种奖惩机制，对当前两个种群之间的交流给予及时的评价和反馈。

为了对两个种群交流进行评价，首先定义评价算子F如下：

其中，Lbest为当前最优路径，LExp为期望路径（TSPLIB库中的标准值），γ为调节因子。

评价后需要做出相应的反馈措施，则定义动态奖惩模型如下：

种群交流后，根据种群A或者种群B的当前最优路径与期望路径求解出评价算子，若评价算子F∈[0,φ]，则进行奖励，从而加快算法的收敛速度；否则进行惩罚，增加算法的多样性，避免陷入局部 最优。

基于奖惩策略的信息素更新机制如下：

其中，当前最优路径在i到j路径上的信息素增量Δτbestij为：

通过动态学习的奖惩模型，当任意种群其评价算子满足权重因子的范围，根据所属范围不同，对其进行动态奖励，在加快算法的收敛速度的同时避免了算法陷入局部最优，最终使其能以较少的迭代次数搜索到最优解。若任意种群的评价算子不满足权重范围，对该种群进行惩罚，减少最优路径上的信息素，加强蚂蚁的探索能力，从而增加算法的多样性。

3.3 算法流程

Algorithm:DACO-DL for the TSP

1.Procedure DACO-DL()

2.Begin:

3.initialize the pheromone and the parameters;

4.while(termination condition not met do)

5.#Algorithm:MMAS

6. foriter1←1 toncdo

7. fori←1 tomdo#mas ants’number

8. forj←2 tondo#nas cities’number

9. Construct ant solutions

10. end for

11. end for

12. if(no stagnation)do

13. Update pheromones

14. else

15. Reactive restart

16. end if

17.end for

18.#Algorithm:SA-MMAS

19.While(T＞Tnc)do

20. fori←1 tom

21. forj←2 tondo

22. Construct ant solutions

23. end for

24. end for

25. fori←1 tomdo

26. if(Better than the current solution)do

27. Change to new solution

28. end if

29. end for

30. Update pheromones

31. Adopt tempering mechanism

32.iter2++

33.end while

34.if(iter1=iter2=p)#pis the multiple ofnc

35. Exchange pheromone

36.end if

37.k++

38.end while

#note:①MMAS and SA-MMAS in parallel

②nc×k=iter2×k=R#Ris the total number of iterations

分析上述算法发现DACO-DL的时间复杂度具体为O((m×(n-1)+n)×nc+(m×(n-1)+m+n)×iter2)×k,其最大时间复杂度为O(m×n×R)；MMAS时间复杂度为O((m×(n-1)+n)×R)，其最 大时间复杂度O(m×n×R);SA-MMAS时间复杂度为O((m×(n-1)+m+n)×R),其最大时间复杂度为O(m×n×R)。可见本文算法时间复杂度与MMAS、SA-MMAS比较并未改变。

4 实验仿真

为了验证本文算法的有效性，选取TSPLIB标准库中17个经典实例进行实验仿真。目前多数文献在小规模TSP问题皆能取得较好的效果，但是对于中大规模TSP问题求解效果较差或者不进行论述。本文使用Matlab2014a软件对小规模以及中大规模的TSP城市都进行了较为详细的对比实验。

ACS、MMAS是蚁群算法中应用最为广泛的算法之一，并且本文在MMAS算法中进行了改进，提出自适应模拟退火蚁群算法（SA-MMAS），为此将本文算法（DACO-DL）与SA-MMAS和ACS的性能进行比较。各算法的参数设置如表1，ACS参数设置参考文献[3]，MMAS参数设置参考文献[4]，其中蚂蚁数量m等于城市数量n。

4.1 问题求解及对比

Table 1 Parameters setting表1 参数设置

为了较好地比较算法的性能，从解的质量、收敛速度、平均解这三方面进行比较，分别用DACO-DL、SA-MMAS、ACS对TSPLIB中17个典型实例进行10次实验，实验结果如表2。

在表2中，标准最优解为TSPLIB实例中当前最优路径长度，最优解为10次实验所求得的最优解，偏差为最优解与当前最优解的偏差程度，迭代次数为算法取得最优值的迭代次数，平均解为10次实验所求的最优解与标准解偏差的平均值。

Table 2 Comparison of algorithm performance表2 算法性能对比

续表2

本文选取几个不同规模城市对比分析最优解偏差，如图2所示。在大中小规模的TSP问题中，本文算法搜索到的最优解偏差小于SA-MMAS、ACS，在中小规模的TSP问题上本文几乎能找到标准最优解。由表2统计分析DACO-DL的偏差均值为0.21%，SAMMAS的偏差均值为0.63%，ACS的偏差均值为0.58%。即在总体求解精度上DACO-DL相比单种群的SA-MMAS、ACS有所提升。

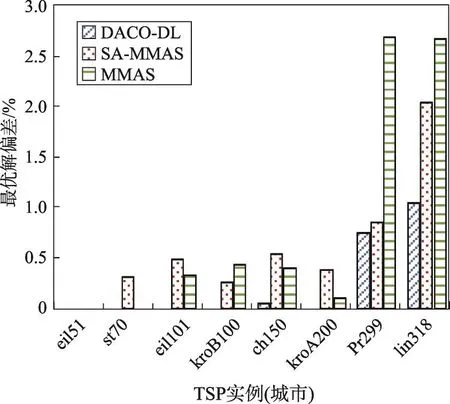
Fig.2 Deviation of optimal solution图2 最优解偏差

下面选取几个实例进行详细说明。对于kroB150，DACO-DL、SA-MMAS、ACS皆取得最优解26 130，但是DACO-DL在迭代100次找到最优解，SA-MMAS迭代359次后寻到最优解，ACS迭代了1 963次找到最优解，可见DACO-DL收敛速度明显优于SA-MMAS、ACS。对于kroA200：DACO-DL在迭代284次后找到最优解22 141，虽然其收敛速度比ACS慢，但是DACO-DL能找到当前最优解，而ACS并没有找到最优解。对于lin318，DACO-DL、SA-MMAS、ACS找到的最优解与标准最优解间存在误差，但是相对而言DACO-DL以较少的迭代次数搜索到的最优解优于所对比的算法。综上分析，DACO-DL能够较强地跳出局部最优，一定幅度地增强了种群的多样性。图3为DACO-DL在17个典型TSPLIB实例的最优路径图。

为了对求解质量更进一步测试，本文选取某几个城市各进行10次实验，统计解的平均误差如图4，明显看出，对于中大规模城市，本文算法平均误差较SA-MMAS、MMAS有显著提高，表明算法有较好的稳定性和鲁棒性。

4.2 收敛速度对比

为了更加直观地对比各个算法的性能，在17个TSPLIB实例中选取不同规模的城市如：eil51、eil101、kroA100、kroB150、ch150、kroA200，比较算法的收敛速度。

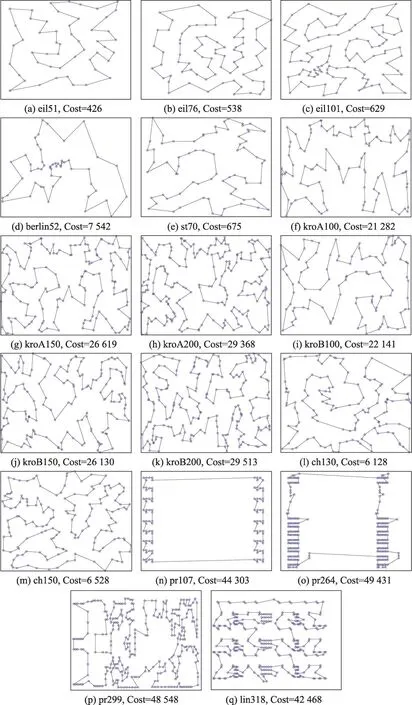
Fig.3 The shortest path图3 最短路径

Fig.4 Average error图4 平均误差

图5中对于eil51、kroA100、kroB150，DACO-DL、SA-MMAS、ACS的最优解皆等于标准最优解，但是DACO-DL的收敛速度优于另外两个算法。对于eil101，DACO-DL以最少的迭代次数搜索到标准最优解；对于kroA200，虽然DACO-DL迭代次数较多，但其最优解优于SA-MMAS、ACS；对于ch150，DACODL的最优解为6 531，标准最优解为6 528，虽然存在误差，但是本文算法在该城市的最优解优于另外两个算法，且找到最优解的迭代次数也是最少的。结合表2可以看出在大多数TSP问题上，DACO-DL能够以最少的迭代次数找到最优解，除了eil76、kroA200、kroB100、kroB200，DACO-DL找到最优解的迭代次数较多，但其找到的解均优于SA-MMAS、MMAS。因此从整体上看，DACO-DL具有较高的收敛速度，同时具有较好的多样性。

5 结束语

Fig.5 Comparison of convergence speeds图5 收敛速度对比

在对蚁群算法的深入研究后，本文提出了动态学习机制的双种群蚁群算法，通过在双种群中加入Q-learning的思想，即在两个种群交流后，对这种交流行为通过奖罚机制给予及时的反馈，从而激发两个种群的开发和探索能力。在求解精度上较对比算法有所提高，在收敛速度上最优的情况比对比算法快了数倍，经过多次在不同规模的TSP问题上的实验，表明了本文算法是有效可行的，对比单种群的蚁群算法，收敛速度以及求解精度都有所提升。由于本文算法并未对蚁群中的交流方式进行深度的研究，在后期工作中会进一步研究种群交流方式，并用基础测试函数进行测试，从而进一步提高并验证算法的性能。