《九章算术》勾股章及其刘徽注中的变式思想①

齐春燕 汪晓勤

(1. 岭南师范学院数学与统计学院 524048; 2.华东师范大学教师教育学院 200062)

众所周知，变式教学是我国传统的教学方式.在教学过程中，教师在保持概念、公式、定理、图形等的本质属性不变的前提下，通过改变概念的表述方式、变换问题的条件和试题的内容和形式、改变图形的形状、位置和大小等在不变中求变，在变中求不变，引导在求异、思变中创新，以培养学生良好的创造性思维品质和创造性学习的能力.鲍建生等认为，用于构建特定经验系统的变式，通常来自问题解决的三种拓展[1]：(1)一题多变；(2)一题多解；(3)一法多用.

变式思想并非现代教育的产物.沈康身先生在介绍中算家的“教学思想”时，曾简要提及一题多解方面的工作[2].本文对《九章算术》勾股章及其刘徽注进行深入分析，试图较全面地揭示其中的变式思想，以拓展教育取向的数学史研究的内涵.

1 《九章算术》勾股章的内容

《九章算术》是我国最重要的数学经典之一，书中包含246个问题，这些问题可分为九类，形成九章.其中，勾股章专门讨论有关直角三角形问题，含24问，由三部分组成.第1-13问为勾股定理的应用题，具体内容是已知a,b,c,a+b,b+c,a+c,b-a,c-a,c-b中的两个元素，求其他元素；第15-20，22-24问为相似直角三角形的应用题，包括勾股容方、勾股容圆以及其他测量问题；第14和21两问为勾股数问题.

设a,b,c分别为(小)直角三角形的勾、股、弦，d为直角三角形内接正方形的边长，x,y分别为直角三角形内接长方形的长和宽，D为直角三角形内切圆的直径，24个问题[3]的相关信息见表1.

表1 24个问题相关信息表

续表

续表

2 一题多变

一题多变是题目结构的变式，通过改变题目的条件或目标，从不同角度、不同方面揭示题目的实质.美国学者希尔佛(Silver)等人[4][5]的研究表明，根据已有问题提出新问题的具体策略有四种：

(1)条件操作，即改变现有问题的已知条件，而保持所求目标不变；

(2)目标操作，即改变现有问题的所求目标，而保持已知条件不变；

(3)对称互换，即将现有问题的条件和目标互换；

(4)新旧链接，即以现有问题的目标为条件，提出新问题.

表2给出基于勾股章第1题提出新问题的具体例子.

表2 基于勾股章第1题的问题提出举例

其中，条件式策略包括两种情形：(1)改变已知条件中的具体数据，我们称之为条件操作Ⅰ；(2)改变已知条件的类型，称为条件操作Ⅱ.如在直角三角形ABC中，将条件a=5，b=12改成a=8，b=15，即为条件操作Ⅰ；将条件a，b改为a，c-b或c-a,b，但保持目标不变，则为条件操作Ⅱ.如果数据和类型都改变，则仍归为条件操作Ⅱ.

图1给出了勾股章诸问题之间的关系.从图中可见，问题1是所有24个问题的出发点.从该问题出发，通过条件操作Ⅰ得到问题5，通过对称互换分别得到问题2和3.从问题3出发，通过条件操作Ⅱ，得到问题11.从问题2出发，通过条件操作Ⅰ和Ⅱ，分别得到问题4、6和13.从问题13出发，通过对称互换，得到问题14.从问题6出发，通过条件操作Ⅰ，得到问题7-10，各问题通过条件操作Ⅱ，得到问题12.

图1 勾股章诸问题之间的联系

从问题1出发，通过目标操作，得到问题15和16.从问题15出发，通过条件操作Ⅰ，得到问题19.从问题19出发，通过条件操作Ⅱ，得到问题20.从问题15出发，通过对称互换，得到问题17.从问题17出发，通过条件操作Ⅱ，得到问题18，21-24.

另一方面，虽然从问题1出发，通过目标操作得到问题16，但问题16的解决是建立在勾股定理基础上的，因为直角三角形内切圆直径需要用直角边和斜边共同来表达.也就是说，从问题1到问题16，也隐含了新旧链接的策略.

由此可见，希尔佛等所总结的四种问题提出策略并非现代人的创造，而是早已为《九章算术》的编撰者所用.

3一题多解

三国时期数学家刘徽在注释《九章算术》时十分重视一题多解，典型的例子是勾股容方和勾股容圆公式的推导.

3.1 勾股容方公式

方法1：割补法

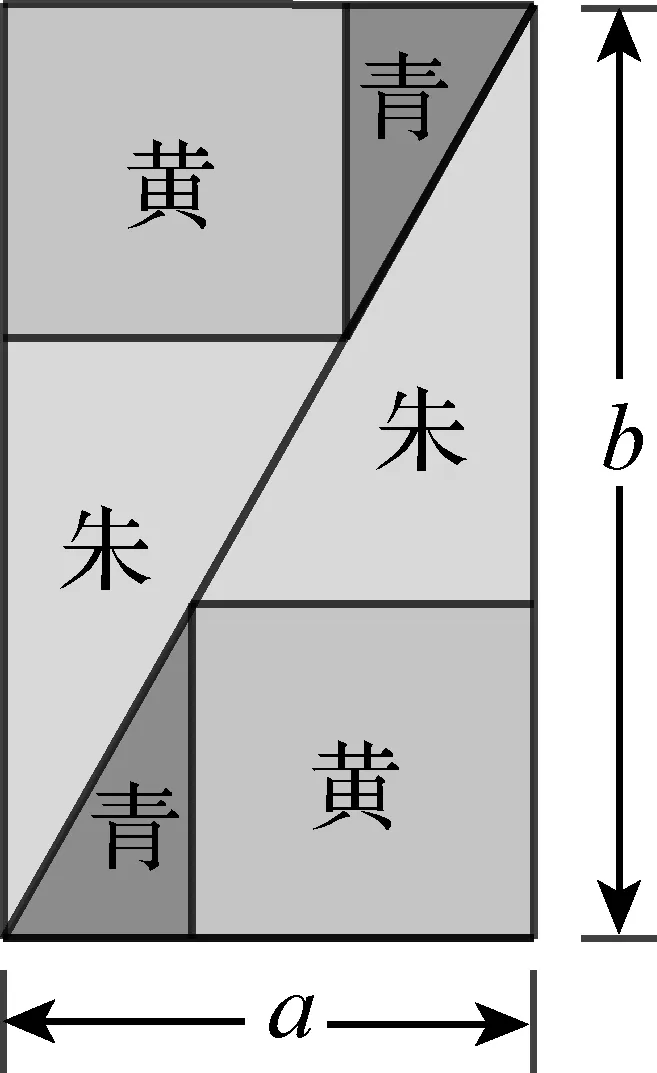
图2

图3

方法2：比例法

如图4，设勾上小直角三角形的直角边长为a1和b1，股上小直角三角形的直角边长为a2和b2，则因a:b=a1:b1，故(a+b):b=(a1+b1):b1，但a=a1+b1,b1=d，故(a+b):b=a:d.

图4

3.2 勾股容圆公式

方法1：割补法

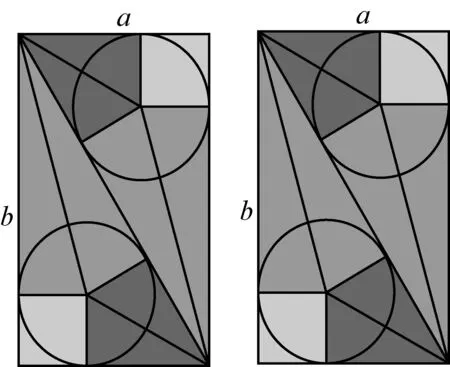
图5

图6

方法2：比例法

图7

如图7，圆O为Rt△ACB的内切圆，过圆心O作斜边AB的平行线，分别交AC和BC于A′和B′，易证AA′=OA′，BB′=OB′.因Rt△A′EO～Rt△ACB，故有

由等比定律得

(1)

同理，由Rt△ODB′～Rt△ACB，可得

(2)

图8

4 一法多用

勾股章第17-24问均为测量问题(表1)，这些问题都可归结为直角三角形内接长方形问题.如图4所示，利用勾上小直角三角形(青幂)、股上小直角三角形(朱幂)以及整个直角三角形两两之间的相似性，可得

(3)

故已知a1，b1，a2，b2，a和b中的三个，可求得其他未知项.第17-20、22-24诸题均通过上述方法求解.

5 结语

根据以上分析，我们得到如下结论：《九章算术》勾股章的问题是以第1题(已知勾、股求弦)为出发点，通过条件操作、目标操作和对称互换三种策略编制而成，体现了精彩的一题多变的变式思想；所有测量问题均利用“相似直角三角形对应边成比例”这一性质来解决，体现了一法多用的变式思想.刘徽在推导勾股容方和勾股容圆公式时采用了不同的方法，体现了一题多解的变式思想.因此，在我国，数学教育中的变式思想至迟可以上溯至《九章算术》成书的时代.

在刘徽之后，中算家们继续运用变式思想，不断提出和解决新的勾股问题，形成了一个独特的课题，即“勾股算术”.因此，变式思想在我国数学教育史上历史悠久、绵延不绝.至此，我们不难理解为什么变式教学是我国传统的教学方式了.追溯变式思想的历史渊源，我们也获得了重要的启示，一个国家或民族的数学教育特色，必定是传承历史的结果；只有民族的，才是世界的.