列车轨道曲线拟合算法改进研究∗
李卫东 高樱莺
(大连交通大学电气信息学院 大连 116028)
1 引言
近年来,基于北斗Ⅱ卫星的定位技术凭借着其操作简便、效率高、精度高的优势,逐渐成为采集轨道定位数据的主流方式之一[1]。利用轨道电子地图可视化,车载设备可以了解线路信息[2];列车定位系统可以对定位传感器的输出进行校验,检测故障;通过地图匹配,可以有效地校正定位误差并提高整个系统的完整性;在电子地图中保存应答器及信号机的信息,可以实现虚拟应答器和虚拟信号机,从而大大降低列车定位系统的成本[3]。因此,拟合高精度轨道曲线数据将对列车定位起到重要作用。
2 轨道定位数据特点
由于铁路线路往往是沿线穿越城市、平原、高山和河流等,这些环境因素会导致获取的轨道定位数据出现误差。利用北斗Ⅱ卫星的定位技术获取轨道定位数据时,因为卫星的星历及时钟的误差、用户接收机精度的误差、电离层信号的传播延迟及多路径效应等,使得卫星信号、传输信号和地面设备接收的信息均有误差,所以定位精度仅为0m~10m(95%置信度)[4]。采集的大量基础数据不可避免地存在误差及异常,使得测量数据的可靠性和可用性下降。在拟合曲线之前都需要对基础数据通过人工剔除、采用小波变化去噪、采用卡尔曼分别对多次采集同一轨道数据滤波等方法,方能得到准确的列车位置信息。
针对测量数据构造拟合曲线的常用方法有Fer-guson曲线、三次Bezier曲线及B样条曲线等[5],在实际应用中这些方法都是只能对一条曲线处理,但在实际生活中的铁轨往往是横纵复杂,在交叉轨道处和平行轨道的地方均会有两条或者两条以上的线路组成,因此在处理中计算复杂度增加[6]。在本文中采用逻辑回归改进模型正是利用了数据的误差特性来实现高精度轨道数据生成,提出在线学习的逻辑回归改进模型,在同一时间能对多条轨道曲线拟合,在保证精准度的同时降低时间复杂度。在逻辑回归中,引入二分类概念,将定位位置信息在曲线左边位置点含有纵轴正误差,定义为正向类;将曲线右边位置点含有纵轴负误差,定义为负向类,通过最速下降法优化加快收敛曲线拟合生成轨道曲线数据,该改进算法不受外界环境影响,在隧道等信号较弱环境中仍然适用的优点[7]。
3 拟合列车轨道曲线数据原理
3.1 轨道曲线数据模型
列车轨迹的生成主要通过历史定位数据训练模型,逻辑回归拟合出一条曲线h,用这条直线对新的定位数据进行预测。其中X 表示历史定位数据点集,θ表示曲线系数集合。

在逻辑回归中,首先引入二分类概念,将历史定位位置信息在标准轨道曲线左边位置点含有纵轴正误差ε,定义为正向类;将曲线右边位置点含有纵轴负误差-ε,定义为负向类。则因变量y∈{0 ,1} ,其中0 表示负向类,1 表示正向类,利用历史带有{0,1}标签的数据训练,构造决策函数,构造逻辑回归模型所做的假设是:
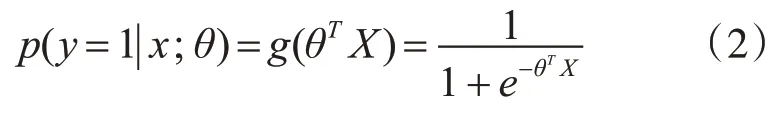
这里的g(h)是sigmoid函数,其数学形式是:

相应的决策函数为y*=1,if P(y=1|x)>0.5,选择0.5 作为阈值是一个一般的做法,实际应用时根据实际情况可以选择不同阈值,如果对正例的判别准确性要求高,可以选择阈值大一些;如果对正例判别准确性要求低,则反之[8]。
由于线性回归是连续的,可以使用模型误差的的平方和来定义损失函数求解参数。但是逻辑回归不是连续的,自然线性回归损失函数定义的经验就用不上了。不过可以用最大似然法来推导出损失函数。确定了模型的数学形式后,需要使用最大似然估计,即找到一组参数,使得在这组参数下,我们的数据的似然度(概率)越大,去求解模型中的参数[9]。
按照二元逻辑回归的定义,假设样本输出是0或者1两类。那么:
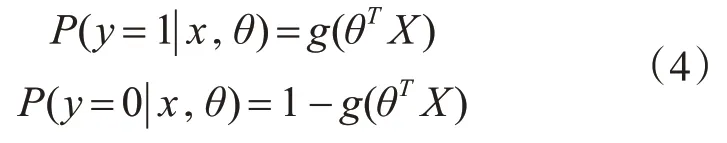
把这两个式子写成一个式子,就是:

在模型中,似然度可表示为式(6)。

等式两边同时取对数可以得到对数似然度:

在本文采用梯度下降法。梯度下降又叫作最速梯度下降,是一种迭代求解的方法,通过在每一步选取使目标函数变化最快的一个方向调整参数的值来逼近最优值。基本步骤如下:
1)选择下降方向(梯度方向,∇J(θ));
2)选择学习率,更新参数θi=θi-1αi∇J(θi-1);
3)重复以上两步直到满足终止条件。
其中损失函数的梯度计算方法为

沿梯度负方向选择一个较小的步长可以保证损失函数是减小的,另一方面,逻辑回归的损失函数是凸函数,可以保证我们找到的局部最优值同时是全局最优[10]。
3.2 轨道拟合模型改进
对于该算法改进问题,存在多种思路[11],为了求得确定多条列车轨道轨迹(判定边界),很容易可以从sigmoid 函数看出,当θT X>0 时,y=1,否则y=0。θT X=0 是模型隐含的分类平面,在高维空间中,我们说是超平面。逻辑回归本质上是一个线性模型,但是,这不意味着只有线性可分的数据能通过LR求解,实际上,可以通过特征变换的方式把低维空间转换到高维空间,而在低维空间不可分的数据,到高维空间中线性可分的几率会高一些[12]。
改进算法利用高斯贝叶斯模型先对数据的联合分布建模,再通过贝叶斯公式来计算样本属于各个类别的后验概率,生成模型和判别模型:
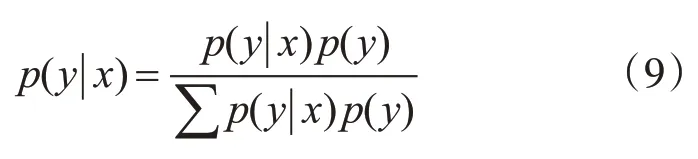
通常假设P(x|y)是高斯分布,P(y)是多项式分布,相应的参数都可以通过最大似然估计得到[13]。在本文中涉及的是正误差和负误差定位点数据,只存在二分类问题,通过简单的化简可以得到:

其中μ1μ0代表正、负类数据集平均数,σ1σ0代表正、负类数据集方差,如果σ1=σ0,二次项会抵消,我们得到一个简单的线性关系:

由上式进一步可以得到:

3.3 轨道曲线拟合
在实际应用中,往往只知道北斗卫星定位系统采集的大量基础数据,不可避免地存在误差及异常,使得测量数据的可靠性和可用性下降。
1)经过预处理的数据点集作为在线学习输入,训练生产轨迹曲线数据模型。
2)先将获取的列车位置信息根据历史定位数据训练模型判断正负误差后二分类。
3)通过最速下降法加快收敛曲线拟合,拟合出误差最小的列车轨道曲线数据。
4 仿真与结果分析
列车轨道拟合准确性是由历史定位数据准确度和在线学习模型参数共同决定的。其中在隧道等信号较弱的地方获取的位置信息为缺失或者错误信息是整个列车位置估计误差主要来源[14]。为了验证算法的有效性及合理性,在本文根据北斗Ⅱ卫星接收机设置2s 接收一次数据[15],以哈尔滨西站的经纬度坐标为起点基准位置,列车实际运行139.86km,列车最高时速200km/h,平均车速为99.90km/h 的条件下,北斗Ⅱ卫星接收机设置2s 接收一次数据,以哈尔滨西站的经纬度坐标为起点基准位置,列车实际运行139.86km,分别采集了3 个历史时刻的数据组,共1800 个北斗Ⅱ卫星的测量数据点,其中1200 个训练数据训练模型,600 个测试数据,过程如下[16]:
1)将测量数据从CGCS2000 坐标系转换到BJ-54坐标系
我国北斗定位系统采用的是CGCS2000 坐标系,而在实际应用中GIS 数字地图采用的主要是BJ-54 坐标系[17]。因此,北斗卫星测量的结果不能直接使用,必须经过相应的坐标转换。本文采用三参数转换法,将CGCS2000 坐标系统转换到BJ-54坐标系,其转换参数可以采用WGS-84 坐标系统到BJ-54 坐标系统的转换参数,在坐标变换的过程中不可避免的会产生一些误差,一般认为由坐标转换带来的误差不超过10m[18]。本文将北斗卫星测得的经纬度信息转换成公里标的结果如表1所示[19]。

表1 坐标转换结果
2)BJ-54坐标转换相同尺度坐标
在面对多维特征问题的时候,为了梯度下降算法更快地收敛,需要通过式(10)保证这些特征都具有相近的尺度[20]。

其中,μn为数组{x1,x2,x3,…xn} 的平均数,Sn为数组{x1,x2,x3,…xn} 的标准差。

表2 同标准尺度下坐标
4.1 比较改进逻辑回归模型拟合曲线和逻辑回归拟合误差率
首先我们将历史定位数据通过训练模型进行二分类如图1 示,然后通过最速下降法求解参数拟合列车轨道曲线如图2 所示,并且与未改进算法比较结果如表3所示。
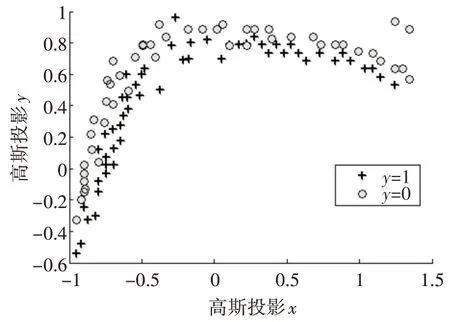
图1 一般轨道定位数据二分类图

图2 一般曲线轨道拟合

表3 实验集误差评价指标
4.2 改进算法对复杂轨道曲线拟合
1)平行轨道拟合
图3 为平行轨道定位数据二分类图,图4 为平行轨迹拟合曲线,从图5 中我们能看出在线学习方法对轨道拟合准确度可以达到92.5%,步长lambda有效可变范围是0~0.03。

图3 平行轨道定位数据二分类图

图4 平行轨道拟合
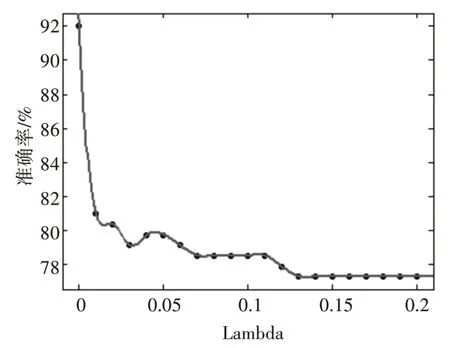
图5 在平行轨道拟合中步长lambda大小对机器学习准确率关系
2)交叉轨道拟合
同上,图6 为交叉轨道的定位数据二分类图,图7 为交叉轨道曲线拟合,从图8 中我们能看出在线学习方法对轨道拟合准确度可以达到93%,步长lambda有效可变范围是0~0.2。

图6 交叉轨道的定位数据二分类图

图7 交叉轨道拟合
从仿真数据及验证的结果得出:
1)在一般曲线轨道、交叉轨道、平行轨道等复杂情况的可行性;在合理选择收敛学习率限差,本文算法能够快速、准确拟合轨道曲线数据,并保证拟合度准确性达到90%以上,在实际应用中有一定价值。

图8 在交叉轨道拟合中学习率lambda大小对机器学习准确率关系
2)分析得出在两条曲线以上且相关度越高的情况下,如:交叉轨道、平行轨道,学习率Lambda变化对轨道拟合准确度越敏感,有效变动范围越小。
3)逻辑回归改进算法解决了多条曲线拟合问题,简约了曲线拟合时间复杂度,克服了局部极值;不受外界环境影响,在隧道等信号较弱环境中仍然适用。
5 结语
本文针对采集的历史定位数据拟合列车定位轨道曲线数据问题,提出改进的在线学习的逻辑回归模型,通过最速下降法优化加快收敛曲线拟合轨道数据及轨道线路表示。仿真数据验证结果表明,本文所述算法能够以较高的拟合精度实现轨道线路描述,且研究学习率Lambda 变化对拟合度的影响,大大降低多条曲线拟合时间复杂读,为高效高性能的列车定位及列车运行控制提供支撑和保障。在今后的研究方向是将该算法结合GIS(Geographic Information Systems,地理信息系统)技术,生成轨道曲线电子地图[21]。

