基于单历元的三频整周模糊度确定算法∗
沈笑云 杨丽萍 焦卫东
(1.天津市智能信号与图像处理重点实验室 天津 300300)(2.中国民航大学 天津 300300)
1 引言
2017 年5 月27 日,北斗“一带一路”应用研讨会在上海国家会展中心召开,以推动北斗系统应用与创新合作为目的,其中北斗RTK(real time kinematic)产品在印度的应用在会议上被讨论。RTK定位技术被应用于海基精密进近着陆,飞机离舰10 海里范围内通过数据通信链路接收到舰上的观测值,可通过RTK技术确定飞机位置[1]。当RTK数据通信链路范围在15km 内才能进行精确定位,并且离基站距离越远,精度越低[2]。超过50km 时,单历元解一般只能达到分米级的定位精度[3]。RTK是一种采用载波观测量的相对观测定位方式,它具有实时的数据传输链路,使得移动用户能够实时地获得高精度定位结果,而获得高精度定位结果的关键问题是如何快速、正确地固定整周模糊度[4]。
针对整周模糊度解算问题,国内外学者提出了多种方法:如模糊度函数法[5]、最小二乘模糊度搜索法[6]和最小二乘模糊度去相关法[7]等,这些方法均是基于双差或三差观测方程解算整周模糊度,其缺点在于至少要知道一个参考站的观测信息,且其精度受到长短基线的影响[8],解算效率较低。鉴于此原因,基于多频组合进行周跳探测和模糊度解算的方法应运而生,其中使用最广泛的多频组合是Melbourne 和Wubbena 提出的Melbourne-Wubbena组合(MW 组合)和码伪距/载波相位组合,MW 组合方法可用于周跳的探测与修复[9],码伪距/载波相位组合方法可用于整周模糊度的确定[10~11]。而采用三频观测值能组成更多波长更长、噪声较小的观测值;通过依次固定超宽巷、宽巷、窄巷模糊度,可以实现模糊度的快速固定[12]。Hatch R[13],李博峰[14]等研究人员利用模糊度固定后的两个超宽巷与一个窄巷组合构成无几何无电离层组合观测值,然后通过多个历元仿真数据平滑固定窄巷模糊度,从而实现模糊度的快速固定。高旺[15]等研究了基于三频无几何模型的北斗系统网络RTK 方法,主要实现了超宽巷和宽巷模糊度的准确固定,并且具有较高的解算效率,通过观测值组合的方法固定模糊度,都存在未对原始频率进行模糊度固定。鉴于上述问题,应充分利用三频观测信息,对三频整周模糊度解算进行研究。本文基于北斗系统B1、B2、B3三个频段及GPS 系统L1、L2 两个频段的实测数据,在双频宽窄巷方法求解模糊度的基础之上,利用三频载波相位整周模糊度之间的整数线性关系,提出三频单历元零基线整周模糊度确定方法。通过对实测BDS/GPS零基线三频数据进行计算仿真分析,验证上述方法的有效性。
2 宽窄巷方法
宽窄巷方法[10~11]也称MW 组合方法,1985 年由Melbourne 和Wubbena 提出,多应用于GPS 系统周跳探测与修复和确定GPS 系统整周模糊度。为了便于说明确定整周模糊度和周跳探测及修复的方法,先给出载波相位和码伪距的观测方程,简明起见系统误差仅考虑对流层延迟、电离层延迟、接收机钟差及观测噪声。
载波相位观测方程为

码伪距观测方程为
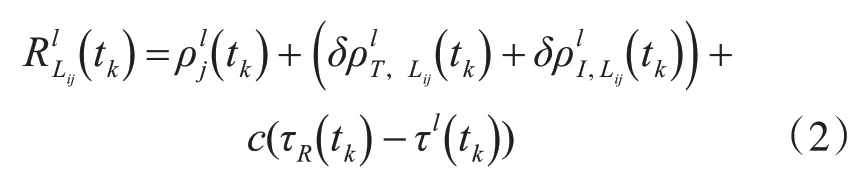
其中为观测历元时刻,为卫星到接收机之间的 长真,f实Li为距载离波,的频 为率载波相为位接模收糊机度钟,差,为τS载 为波 时波 钟钟差,为对流层折射延迟,为电离层折射群延迟,c为真空中的光速表示北斗系统载波标识(i=1,2,5),j为接收机标识,l为卫星标识。
根据式(1)和式(2)分别写出L1和L2载波相位观测值及L1与L2载波上码伪距观测值观测方程的显示表达式:


令宽巷组合观测值为

则对应的宽巷组合观测值的模糊度为

令窄巷组合观测值为

则对应的窄巷组合观测值的模糊度为

由宽巷窄巷组合观测值的模糊度可得两个频率的模糊度:
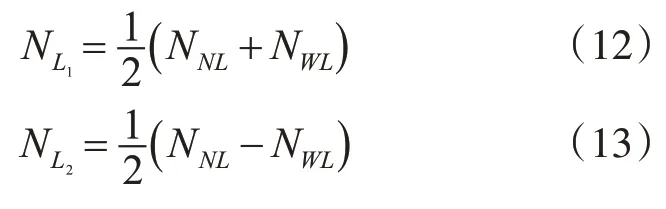
3 本文方法
由于宽窄巷方法只能处理双频观测数据的缺点,本文提出的算法在宽窄巷方法基础之上,引入第三个频率的伪距观测方程和载波观测方程,根据式(3)和式(5)分别补充写出L5载波相位观测值及载波码伪距观测值观测方程的显式表达式:

令与频率无关的总误差总和为Δρ,则卫星到接收机之间的距离ρ'=ρ+Δρ。根据式(3)和式(5)可以得到:

根据式(9),L1和L2的宽巷组合,L1和L5的宽巷组合分别为

通过式(3)~(6),式(15)~(18)解得三个频率的整周模糊度分别为
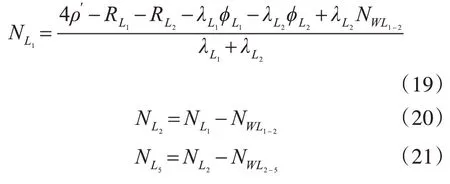
由此得到单频载波的整周模糊度值。
此方法充分利用了观测方程,且易于程序实现,消除了卫星钟差和接收机钟差的影响,卫星星历误差和大气延迟误差的影响也得到大幅度的削弱。此方法也可以应用与GPS 双频系统确定整周模糊度,可将第三频率的伪距和载波观测信息记为零,视为本文算法的一个特例。
4 实验验证与分析
利用两台多系统多频点接收机于司南导航上海市闵行区实验中心(北纬31.174300603°,东经121.387866640°)与2014 年7 月9 日采集一组GPS/BDS/GLONASS 三星零基线静态数据,采样间隔10s,数据长度约2h。观测的实际运行卫星的原始观测数据为例进行实测数据分析,验证本文推导的整周模糊度解算的正确性,利用不同接收机接收到的卫星信号实测瞬时多普勒数据,得到积分多普勒值,然后通过卫星信号原始载波相位变化值和伪距观测值,给出GPS系统和北斗系统整周模糊度和周跳数的实验结果。
4.1 实验参数
表1 为BDS/GPS 系统信号实验环境的主要技术参数。

表1 实验参数
4.2 实验结果
4.2.1 整周模糊度固定
图1(a)、(b)分别为GPS 系统G25 卫星利用宽窄巷法在接收机802182 在L1,L2 载波上的整周模糊度随历元变化曲线,(c)、(d)表示在接收机802443在L1,L2 载波上的整周模糊度随历元变化规律曲线。图中选取了720个历元的整周模糊度值。图2为两个接收机在L1载波上的整周模糊度差值。

图1 G25卫星宽窄巷法求解整周模糊度

图2 G25卫星宽窄巷法求解L1载波模糊度差值
图3 为北斗系统C04 卫星利用宽窄巷法分别在接收机802182和接收机802443两个载波上的整周模糊度随历元变化规律曲线,其中(a)表示接收机802182 上B1 载波的整周模糊度曲线,(b)表示接收机802182上B2载波的整周模糊度曲线,(c)表示接收机802443 上B1 载波的整周模糊度曲线,(d)表示接收机802443 上B2 载波的整周模糊度曲线。图中选取了720个点的整周模糊度值。图4为两个接收机在B1载波上的整周模糊度差值。与图1所示的GPS系统G25卫星对应的整周模糊度差值曲线的趋势相似,说明在接收机放置地点此采样数据时段接收到的北斗数据性能与GPS大致相同。
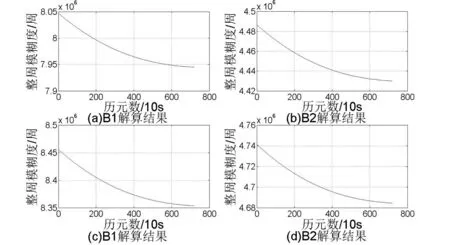
图3 C04卫星宽窄巷法求解整周模糊度

图4 C04卫星宽窄巷法求解B1载波模糊度差值
图5 分别为GPS 系统G25 卫星利用三频模糊度分解法分别在接收机802182和接收机802443两个载波上的整周模糊度随历元变化规律曲线,其中(a)表示接收机802182 上L1 载波的整周模糊度曲线,(b)表示接收机802182上L2载波的整周模糊度曲线,(c)表示接收机802443上L1载波的整周模糊度曲线,(d)表示接收机802443上L2载波的整周模糊度曲线。与图1 所示的GPS 系统卫星利用宽窄巷法解算各载波整周模糊度值基本相近,可验证本文中的三频模糊度分解算法合理。
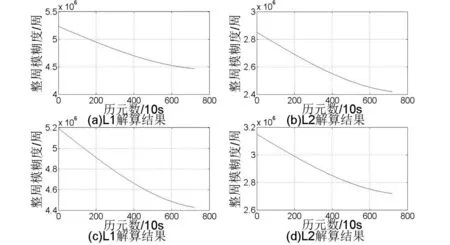
图5 G25卫星三频模糊度分解法求解整周模糊度

图6 G25卫星本文方法求解L1载波模糊度差值
图7 为北斗系统C04 卫星利用三频模糊度分解法分别在接收机802182和接收机802443两个载波上的整周模糊度随历元变化规律曲线,其中(a)、(b)、(c)表示接收机802182 上三个载波的整周模糊度曲线,(d)、(e)、(f)表示接收机802443 上三个载波的整周模糊度曲线。图8 为两个接收机在B1载波上的整周模糊度差值,与图9 所示的GPS 系统G25 卫星对应的整周模糊度差值曲线的趋势相似,也可以说明在接收机放置地点这个时间点接收机接收北斗卫星性能与GPS 卫星性能大致相同。与图4、5、6 所示的利用宽窄巷法解算北斗系统卫星各载波整周模糊度值基本相近,可验证本文提出的三频模糊度分解算法与宽窄巷法求解模糊度的差别在于可以快速同时求解出三个载波整周模糊度值。

图7 C04卫星本文方法求解整周模糊度

图8 C04卫星本文方法求解L1载波模糊度差值
4.2.2 周跳检测
图9 为GPS 系统G25 卫星利用三频模糊度分解法分别在接收机802182和接收机802443两个载波上的周跳数随历元变化规律曲线,其中(a)、(b)、(c)表示接收机802182 上三个载波的周跳曲线,(d)、(e)、(f)表示接收机802443上三个载波的整周跳曲线。图10为两个接收机在L1载波上的周跳数差值。由图可以看出,GPS系统G25卫星L1载波上的周跳数比L2 载波上的周跳数更多;两个载波上大部分历元周跳数均在311~1433 周之间变化;两个接收机同时接收卫星数据虽然同一载波上整周模糊度差值较大,但计算出周跳数差值在大部分历元中不足0.5周的差值。

图9 G25卫星本文方法求解周跳数曲线
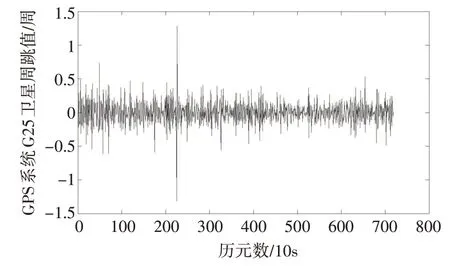
图10 G25卫星本文方法求解L1周跳数差值
图11 为北斗系统C04 卫星利用三频模糊度分解法分别在接收机802182和接收机802443两个载波上的周跳数随历元变化规律曲线,其中(a)、(b)、(c)表示接收机802182 上三个载波的周跳曲线,(d)、(e)、(f)表示接收机802443上三个载波的周跳曲线。图12 为两个接收机在B1 载波上的周跳数差值。由图可以看出,北斗系统C04 卫星B1 载波上的周跳数比其他两个载波上的周跳数更多;三个载波上大部分历元周跳数均在5~12 周之间变化;两个接收机同时接收卫星数据虽然同一载波上整周模糊度差值较大,但计算出周跳数差值在大部分历元中不足0.5周的差值。
本文只给出802182和802443接收机的北斗系统C04 卫星和GPS 系统G25 卫星的整周模糊度曲线和周跳数曲线。其他北斗GEO 卫星的两种曲线性质均与C04 卫星一致;其他GPS 卫星的两种曲线性质均与G25卫星一致,故不再一一赘述。通过比较图11 和图9,在数据采集地区,北斗系统GEO 卫星的周跳值明显小于GPS卫星的周跳值,表明在该地区北斗系统GEO卫星性能好于GPS卫星。
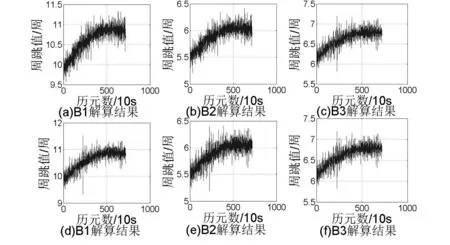
图11 C04卫星本文方法求解周跳数

图12 C04卫星本文方法求解L1载波周跳数差值
表2 中信息为两个定位系统利用两种方法计算整周模糊度的成功率。由于北斗系统的广播星历轨道精度较低,观测值的噪声较大,在进行整周模糊度固定的成功率明显要低于GPS 系统。GPS系统两个频率L1,L2,在利用三频方法进行整周模糊度解算,对于整周模糊度固定没有影响。北斗系统利用三频方法求解整周模糊度成功率明显好于利用宽窄巷方法所求解的整周模糊度。表3 为利用两种方法分别计算北斗系统和GPS 系统相同历元数的整周模糊度求解花费的时间,利用三频方法计算北斗系统或GPS 系统整周模糊度在时间效率上均好于宽窄巷方法。

表2 模糊度固定成功率

表3 计算模糊度时间开销
5 结语
通过仿真验证了本文方法的正确性,表明对零基线三频数据的三频模糊度分解法快速解算载波相位的整周模糊度是可行的;三频模糊度分解法具有更好的固定成功率以及计算效率;在相同地点相同时间不同接收机对同一卫星计算载波整周模糊度结果不同,从而对卫星导航定位的精度产生很大影响。基于本文的研究结论,可将三频模糊度分解法运用于整周模糊度及周跳的快速求解,进行RTK的模糊度初始化结果验证,从而进行动态相对定位。

