一种求解模糊期望值模型问题的有效算法∗
肖 宁
(陕西职业技术学院计算机科学系 西安 710100)
1 引言
为适应不确定规划尤其是模糊规划理论研究和应用的发展,LIU 提出了模糊规划理论并建立了相应的模型及基于经典GA 的求解算法[1~3],许多模糊规划问题因而也得到了有效求解[4~8],鉴于PSO算法的求解优势[9~12],本文作者在不确定规划的求解算法方面也做了一些研究工作[14~16],为了探究更优的求解算法,本文采用随机PSO(一种保证全局收敛的随机微粒群算法[16])并结合模糊模拟技术对模糊规划中的期望值模型问题进行了研究,通过对典型算例的仿真实验,从而为该类问题的有效求解提供了思路,也为另外两类模糊规划和其他不确定规划问题的求解提供了思路。
2 模糊期望值模型
模糊期望值模型(Fuzzy Expected Value Model,FEVM)是Liu[1]所提出来的一类模糊规划,它是使模糊目标函数的期望值在模糊期望值的约束下达到最优的一类规划模型。一直以来对其进行高效求解是工程应用领域中的热点研究问题。
FEVM通常表示如下:
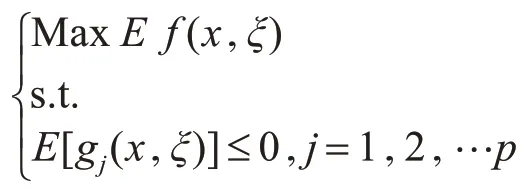
在以上模型中,X表示决策向量,ξ表示模糊向量,表示目标函数表示约束函数。
为达到多个目标的平衡,构造出相应的FEVM目标规划模型表示为
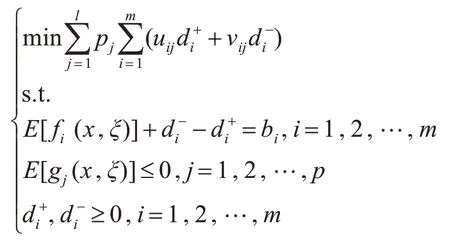
在此,bi是目标i 的目标值,m 代表目标约束个数,p 代表系统约束,是优先因子,它代表了各目标的相对重要性,uij是对应优先级j的第i个目标的正偏差的权重因子,vij是对应优先级j 的第i 个目标的负偏差的权重因子,是目标i 偏离目标值的正偏差,是目标i 偏离目标值的负偏差,l 代表了优先级个数,gj是系统约束中的函数,fi是目标约束中的函数。
3 基本微粒群算法
在PSO 中,微粒群即是D 维空间中问题的潜在解的集合,微粒们依据本身及同伴的飞行经验不断调整自己的位置、速度,用适应值评价解的优劣,不断追随当前、历史最优微粒进行更新,通过不断迭代朝着最好解飞行。微粒i 的第d 维的速度、位置通过下式更新:
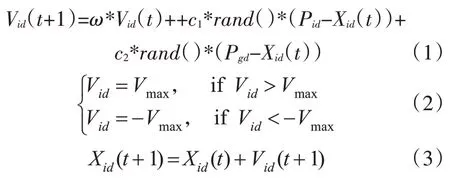
在以上公式中:c1、c2表示飞行的加速常量;均匀分布于[0,1]上的随机数为rand();个体第d 维分量(历史最优位置)为Pid;ω为惯性权重;全局第d维分量(历史最优位置)为Pgd。
4 SPSO算法
在以上的基本PSO 算法中,若ω=0,微粒的飞行速度取决于xi(dt)、pid、pgd,除全局最优位置微粒此时会处于静止状态之外,其余微粒均趋向自身及全局最优位置的加权中心。即微粒群将收缩至当前的全局最优处,类似于一个局部算法;若ω≠0,让微粒形成搜索范围扩展的可能,也就是具备相应的全局搜索能力。全局搜索能力与惯性权重成正比。这表明,惯性权重若是零,式(3)所描述的公式为
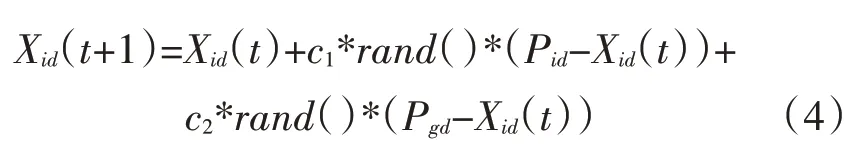
这样,式(4)在加强局部搜索能力的同时,弱化了全局搜索能力。如果X(jt)=Pj=Pg,因为处于历史最好位置的微粒j不可以依据式(4)进化,所以经由随机产生于搜索空间内的微粒把j 微粒替代,和经过Pi、Pg更新之后的其余微粒一同依据式(4)进化;如果Pg与Pj不相等,同时也没有更新Pg,那么依据式(4)进化全部微粒;如果Pg与Pj不相等,但已更新Pg,也就是在f≠j 时,Xf(t+1)=Pf=Pg,那么微粒f 进化终止,于搜索空间内再次随机形成,Pi、Pg更新之后,其它微粒依据式(4)进化。此时,最少存在1 个微粒j 在进化的某些代会把X(jt)=Pk=Pg满足,也就是说,搜索空间最少需重新随机形成1 个微粒,全局搜索能力会因此提高。
5 模糊模拟与SPSO 算法相结合的FEVM模型算法
该类问题求解过程中所采用的SPSO 算法,其核心主要在于模糊期望值函数如何计算,这可以通过模糊模拟来完成,在整个寻优期间,它主要体现在:初始化时期要用到模糊模拟来实现所有微粒适应值的计算;在每迭代中也要利用它计算个体的适应值等。模糊模拟期望值估计算法过程如下:
如果实值函数,表示为f:Rn→ R,ξ=(ξ1,ξ2,…,ξn)是可能性空间(θ,P(θ),Pos)中的n维模糊向量,则(fξ)也是一个模糊变量,其期望值定义为
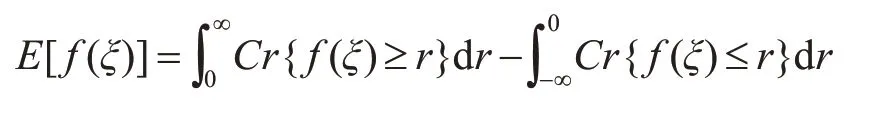
以下的模糊模拟过程用来计算E[f(ξ)]。分别从θ中均匀产生θk,使Pos{θk}≥ε(ε代表了一个充分小的数),并定义vk=Pos{θk},k=1,2,…,N。对任意的r≥0 ,则可信性Cr{f(ξ)≥r}近似等于
对任意r<0 ,可信性Cr{f(ξ)≥r}近似等于
模糊模拟算法的期望值估计算法:
第1步:令e=0;
第2步:分别从θ中均匀产 生θk,使 得Pos(θk)≥ε,令vk=Pos{θk},k=1,2,…,N;
第3步 :置a=f(ξ(θ1))˄ … ˄f(ξ(θN)),b=f(ξ(θ1))˅ … ˅f(ξ(θN));
第4步:使得r从[a,b]中均匀产生;
第5步:若r≥0,令e←e+Cr{f(ξ)≥r};
第6步:若r<0,令e←e-Cr{f(ξ)≤r};
第7步:重复第4至6步共N次;
第8步:E[f(ξ)]=a˅0+b˄0+e⋅(b-a)/N。
SPSO 算法与模糊模拟相结合的求解FEVM 的混合智能算法步骤:
第1步:微粒群初始化:若popsize是微粒数量,那么,把1个随机数形成于决策向量x的可行域内,且对它的可行性进行检验,把该过程进行popsize次重复之后,则获得:xi=(xi1,xi2…xid)i=1,2…popsize 随后再初始化群的最好位置、个体最好位置及所有微粒速度等。
第2步:所有微粒适应值的计算,即计算目标E[g(jx,ξ)],均采用估计算法(模糊期望值模拟)展开。
第3步:若x(it)=pj=pg,则在搜索空间中随机机产生粒子j的位置,并计算其适应值,即计算目标E[g(jx,ξ)](模糊模拟的可信性估计算法)及个体最优值,其他粒子按式(4)进化,并计算它们的适应值,即计算目标E[g(jx,ξ)](模糊模拟的期望值估计算法)及个体最优值。
第4步:pg如果不等于pj,同时没有更新pg,则以式(4)进化所有粒子。
第5步:pg如果不等于pj,但已更新pg,也就是说f 不等于j,导致x(ft+1)=pf=pg,那么粒子f的进化终止,把其位置重新随机形成于搜索空间内,并计算其适应值,即计算目标E[g(jx,ξ)](模糊模拟的期望值估计算法)及个体最优值,其余粒子按式(4)进化。
第6 步:检验更新后粒子的可行性:若可行,则接受并计算它们的适应值,即计算目标E[g(jx,ξ)](模糊模拟的期望值估计算法)及它们的个体最优值,否则则原位置保持原状。
第7步:把全局最优微粒pg找出。
第8步:第3步至第7步重复执行,直到有1 个预设最大迭代次数或足够好的适应值。
第9步:结束迭代,把最优解、对应于最优解的最优值给出。
6 实例仿真
本文所论述方法采用以下典型实例进行验证,运行环境:在PC 机的CPU 的主频:2.5GHz,内存:2GB,操作系统:WinXP,VC++6.0环境下编写、运行代码。
例1考虑如下的单目标FEVM模型[2]:
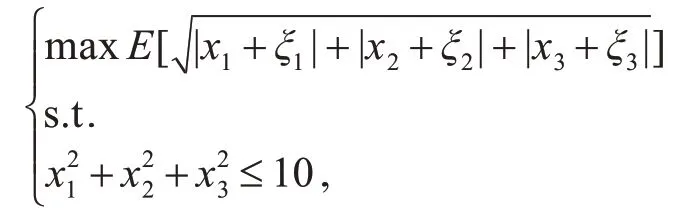
其中ξ1为三角模糊变量(1,2,3),ξ2为三角模糊变量(2,3,4),ξ3为三角模糊变量(3,4,5)。
在本代码中选择和文献[2]相同的参数值:种群规模:30,模拟次数:6000,迭代数目:1000,运行次数:1。
例2考虑如下的FEVM目标规划模型[3]:
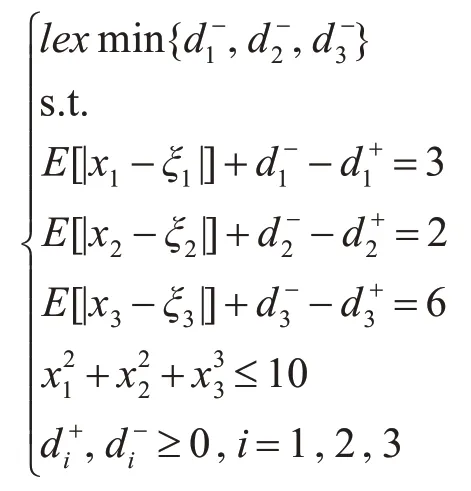
其中模糊变量ξ1为三角模糊变量(0,1,2),ξ2为三角模糊变量(1,2,3),ξ3为三角模糊变量(2,3,4)。
在本代码中选择和文献[3]相同的参数值:种群规模:30,模拟次数:5000,迭代次数:1000,运行次数:1。
在例1中:运行一次的结果如表1所示,对比文献[2]中的数据,文献[2]显然不如本文算法的效果。如图1 所示,为使得迭代过程体现得更直观,把代码运行1 次的整个1000 次的迭代过程每隔20代进行抽样,文献[2]必需1000 代迭代才能获得的最优值,在这种算法中只要到第20 代时便可实现。为规避一次运行所得到的结果的偶然性,把代码进行了10 次运行,每次都是在20 代时就达到与文献[2]相同的优化效果,从60 代开始最优值就开始稳定,其平均值见表1 最后一行。显然,文献[2]最优值不如采用此法所获得的结果。
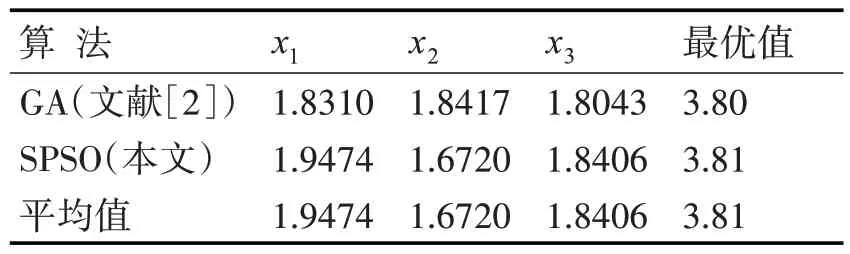
表1 实例1数据比较
在例2 中:运行结果如表2 所示,对比文献[3]中的数据,显然优于文献[3];正如表3 所示,程序10次运行的每一次的结果均优于文献[3]。

表2 实例2结果比较
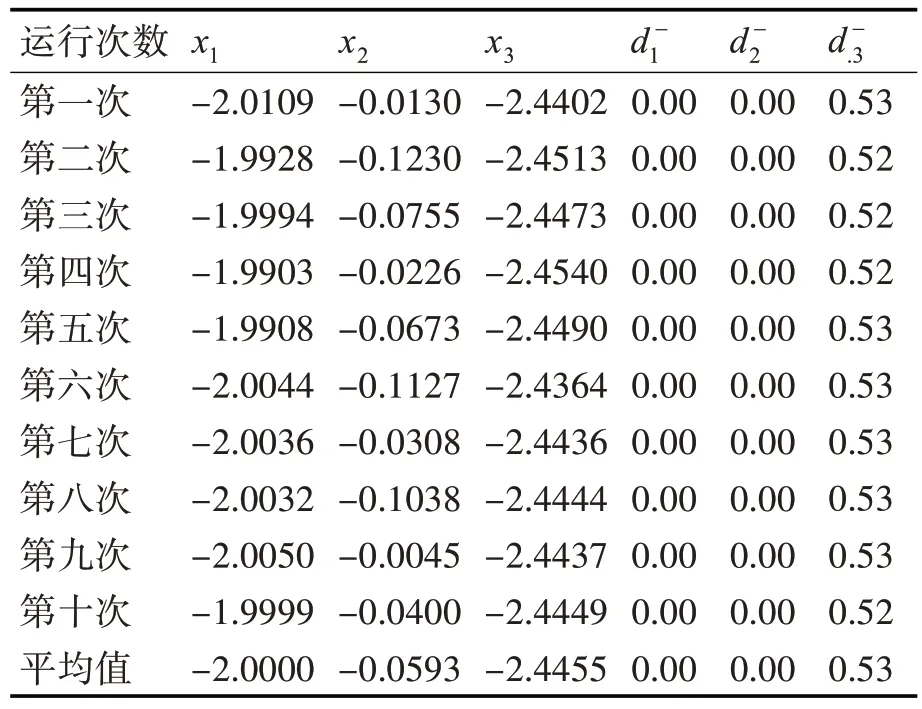
表3 结果统计

图1 实例1迭代过程抽样图
7 结语
FEVM 模型问题是在实际工程应用及科学研究中都有重要意义的不确定规划问题,目前应用普遍的方法是尝试将智能算法用于该类问题的求解,混合智能算法:模糊模拟与SPSO 算法求解FEVM问题是本文描述的主要内容,对比经典的混合智能算法(基于GA 算法)与实例仿真的结果表明,它存在着很好的优化性能;显示了该算法在FEVM 问题中的优势,该算法不仅对连续空间的FEVM 问题求解提供了新的方法,对其他不确定规划问题的求解也有重要的指导意义,同时也拓展了PSO算法研究的应用领域。

