改进型极限学习机模型在粮食产量预测中的应用∗

吴耀东

（新疆工程学院 乌鲁木齐 830091）

1 引言

农业是国民经济发展的基石，而粮食则是社会进步与发展的最基本保障，准确地预测未来一段时间的粮食产量，能够为政府估计未来粮食安全状况进而制定有效政策，实现粮食安全具有重要意义［1～4］。目前较为常用的粮食产量预测方法包括遥感预测法［5］、时间序列预测法［1］、灰色模型法、BP 神经网络［2］和支持向量机（SVM）［6］等。文献［1］和［2］分别利用ARIMA 和BP 神经网络预测粮食产量。文献［6］利用遗传算法优化SVM 模型参数，应用于粮食产量预测。

上述的粮食产量预测方法存在一些不足，比如BP 神经网络的学习速度较慢，并且可能陷入局部最优，影响分类精度；SVM 对大规模训练样本的建模存在计算量大的问题等。极限学习机（ELM）作为一种新型的单隐层前馈神经网络学习算法［7］，具有学习速度快、泛化能力强等优点［8～9］，已经在时间序列预测［10］、模式识别［11～14］等领域得到了应用。

对于ELM，隐节点数目L 对模型预测准确性影响较大，较小的L会降低ELM预测准确性，较大的L会降低ELM 的泛化性能［15］。为了确定合适的隐节点数目，需要计算不同L 下ELM 的预测误差，但每次计算不同L 对应的输出权重时，需要重复计算隐层矩阵的广义逆矩阵，当L 较大时，会增大计算量。为此，推导L 递增情况下输出权重的递推公式，提出增长ELM（GELM）算法，从而有效降低ELM的计算量，实验结果证明了本文提出方法的有效性。

2 增长极限学习机（GELM）

GELM 的思路是从最小的隐节点数目L 开始，按固定数量逐渐增加ELM 中的L，直到满足规定的停止准则，最终确定ELM 中的L。同时，每次增加L时均需重新计算输出权重β，当L 较大时，Η的Moore-Penrose 广义逆矩阵Η†的计算量迅速增加，为此，推导ELM 中L 递增情况下β的递推计算公式，降低ELM的计算量。

2.1 输出权重递推计算

假设ELM 隐节点数目为L 时的隐层矩阵为HL，如式（1）所示。当隐节点数目增加ΔL 时，ELM的隐层矩阵变为]， 其中 ΔHΔL为新增加的ΔL 个隐节点组成的隐层矩阵，如式（2）所示。

式中，ai∈ℝn和bi∈ℝ 表示隐含层参数。对于包含ΔL+L个隐节点的ELM，输出权重为

由式（3）可知，计算βL+ΔL时，需要计算N×（L+ΔL）维矩阵的广义逆矩阵其中N 为样本数量。当L+ΔL 较大时的计算量迅速增加。

为此，推导隐节点数目按ΔL 递增情况下，[HLΔHΔL]†的递推计算公式，可以有效降低计算量。推导过程如下。

式中

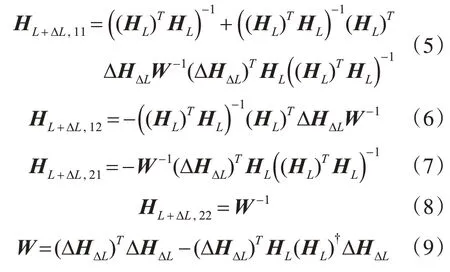
根据式（4）和式（7）～（9），令σ=I-HL(HL)†，可知σΤ=σ，σ2=σ，则

同理，根据式（4）～（6）和式（10），可以计算F为

则式（3）的计算可以变为

2.2 GELM算法流程

步骤1初始化GELM 的模型参数，其中初始隐节点数目为L0，生成由L0个隐节点组成的H0矩阵，如式（1）所示，其中参数ai和bi利用随机生成方式获得。设定单次增加的隐节点数目为ΔL，并令隐节点递增次数k=0。计算初始的输出权重矩阵β0：

步骤2令k=k+1，第k 次增加的隐节点ΔL 对应的隐层矩阵ΔHΔL如式（8）所示。根据式（13）得

步骤3令Hk=［Hk-1ΔHΔL］，Lk=Lk-1+ΔL。计算预测误差

步骤4若errork＜errork-1，转入步骤2；若errork≥errork-1，转入步骤5。

步骤5确定GELM 的隐节点数目为Lk，其对应的输出权重为βk。

3 粮食产量预测流程

基于GELM的粮食产量预测算法整理如下。

步骤1将已知的粮食产量转换成训练样本和参数优化样本，其中为第i年度的粮食产量，τ为嵌入维数。的数据形式与相同。

步骤2根据3.2 节的GELM 算法流程，利用和{建立GELM预测模型。

步骤3为预测第n+1 年度粮食产量，将第n-τ+1 年度至第n 年度粮食产量作为输入向量，计算对应，计算xn对应输出，即为第n+1年度预测值。

4 实例验证

4.1 实验数据

选取全国1960-2015 年的粮食总产量作为实验数据，见表1。由表1 可以看出，1960-2015 年粮食产量总体呈增长趋势。1960-1977 年期间，粮食总产量增长较为缓慢；1978-1999 年期间，粮食产量增长速度较快；在2000 年，粮食产量较前一年出现下降，直到2004 年，粮食产量恢复增长趋势。选取1960-1994 年的产量作为训练样本，1995-2004年的产量作为参数优化样本，优化粮食产量预测模型参数，利用2005-2015 年的产量作为测试样本，检验预测模型的预测性能。训练样本、参数优化样本和测试样本转化成形 式 ，其 中为第i 年的粮食产量，τ为时间序列嵌入维数。

表1 全国1960-2015年的粮食产量

4.2 参数选择

设定GELM 初始隐节点数目L0=50，单次隐节点递增个数ΔL=20。将GELM 用于时间序列预测时，嵌入维数τ影响着预测准确性。分别令τ=2，3，…，10。对于每个选定的τ，计算GELM 对应的参数优化样本预测误差绝对值，选取误差最小值作为每个τ对应的预测误差。则不同τ值对应的预测误差如图1 所示。可以看出，τ=3 时预测误差最小。图2 所示为τ=3 时，GELM 从初始隐节点L0开始，逐步按ΔL 递增隐节点数目，其对应的参数优化样本预测误差。确定GELM的隐节点数目为210。

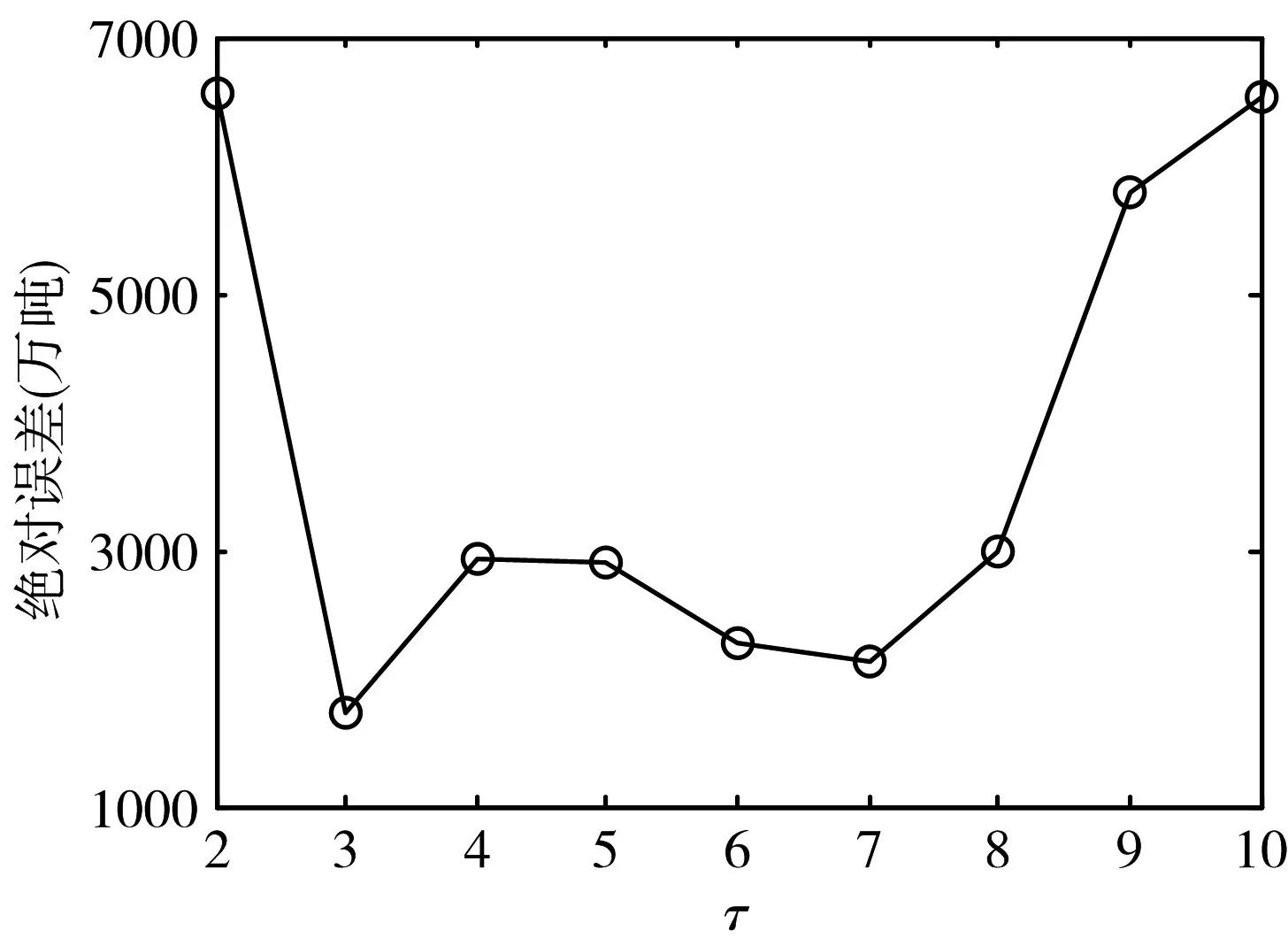
图1 GELM不同τ值对应的预测误差

图2 GELM随隐节点数目递增对应的参数优化样本预测误差

分别采用标准的ELM 和支持向量机（SVM）作为对比方法，其中SVM选用libsvm工具箱中提供的函数。对于ELM 和SVM，时间序列的嵌入维数τ同样需要人为确定。此外，影响ELM 的参数为隐节点数目L，影响SVM 的参数为C 和γ。分别令ELM中的L={50，70，…，300}，SVM 中的C 和γ={2-14，2-13，…，214，215}，采用与GELM 同样的参数寻优方法，得到ELM 和SVM 的最优参数如表2 所示。实验所用计算机为Windows XP 系统，Intel i5 CPU（主频3.5GHz），4GB内存，仿真软件为Matlab R2011b。

表2 不同方法最优参数

4.3 预测结果

三种方法按照表2 的参数建立预测模型，进行50 次蒙特卡洛仿真，计算得到训练样本的平均绝对误差（MAE）如表3 所示。可以看出，相比于SVM，GELM 和ELM 对训练样本的预测准确性较高，说明GELM和ELM对于已知数据的拟合精度较高。三种方法对测试样本的预测结果和预测绝对误差分别如图3 和图4 所示。进行50 次蒙特卡洛仿真，得到三种方法对测试样本的MAE 如表3 所示。对于测试样本而言，GELM 的预测准确性较训练样本偏低，这主要是因为测试样本并没有参与预测模型的建立过程，但是GELM 的预测结果的总体趋势与实际情况相符，说明GELM 在粮食产量预测中的有效性。ELM 和GELM 方法的预测误差较接近，相比之下，GELM 的预测精度略高于ELM，SVM预测误差最大。

三种方法的耗时同样如表3 所示，其中耗时包括参数优化样本寻优时间、训练样本建模时间和测试样本测试时间。可以看出，由于SVM 需要同时优化τ、C和γ三个参数，其耗时最长。ELM和GELM需要更新τ和L 两个参数，对于不同的隐节点数目L，GELM能够利用上一步L对应的隐层矩阵的广义逆矩阵，根据式（19）的递推方式计算当前L 对应的隐层矩阵的广义逆矩阵，继而更新输出权重，而ELM 对每个L 均需要重新计算隐层矩阵的广义逆矩阵，因此ELM的耗时高于GELM。

表3 三种方法的MAE误差和耗时

图3 三种方法对测试样本的预测结果

图4 三种方法对测试样本的预测误差

5 结语

本文提出了基于GELM 的粮食产量预测方法。为了解决ELM 隐层结构优化问题，推导ELM中隐节点数目L 递增情况下输出权重的递推计算公式，从而有效降低ELM 的计算量。粮食产量预测结果表明，GELM 的预测精度和耗时均优于SVM，GELM 的预测精度与ELM 相似，但耗时低于ELM，从而证明本文推导的递推公式可以降低输出矩阵的计算量。实验结果说明本文提出方法可以有效地应用于粮食产量预测。