一种基于密度聚类的分布式离群点检测算法∗

刘亚梅 闫仁武

（江苏科技大学计算机学院 镇江 212003）

1 引言

局部离群点检测算法是数据挖掘中离群点检测的一个重要研究方向。基于小规模数据集的挖掘，离群点往往是被作为噪声除去的，但随着数据规模的不断扩大，大数据技术的日益成熟，从海量数据中挖掘的离群点可不再是噪声和无用点，这些点可以揭示稀有事件和现象、发现有用的信息，成为有意义点。Hawkins［1］的关于离群点的定义得到广泛认可，在相关的研究领域，局部离群点检测算法［2］已经相当成熟，但是面对大量高维的复杂数据时，这些算法的执行效率、检测准确度等方面还存在明显的不足。

迄今，诸多学者采用了许多方法来提高离群检测算法的性能。例如，张天佑［3］提出基于网格划分的高维大数据集离群点检测算法，将高维空间进行网格划分后，对剩余离群点集进行检测，缺点是对高维海量数据进行网格划分时，时效将成指数增长；周鹏等［4］提出一种结合平均密度的改进LOF 异常点检测算法，先根据数据集中数据点的平均密度的分布情况确定的一个异常集D1，然后通过计算离群因子确定另一个个异常点及异常集D2，取D1与D2的交集作为最终的离群集，缺点是对于海量数据来说，其计算效率也会很低；王习特等［5］提出一种高效的分布式离群点检测算法，运用DBSP（Balance Driven Spatial Partitioning）数据划分算法对数据进行预处理，提出了BOD（DBSP-Based Outlier Detection）分布式离群点检测算法，但算法对全局离群点有良好的检测效率，不适用于局部离群点的检测。

Google 提出的MapReduce 是一种用于大规模数据集的并行运算编程模型，能够处理T 级别以上巨量数据的业务［7］。Apache 基金会开发的Hadoop分布式系统能够很好地处理巨量数据，本文中基于Hadoop 平台，应用MapReduce 编程模型实现了一种局部离群点检测算法——基于密度聚类（DBSCAN）的局部离群点检测算法（LOF）。首先根据文献［5］DBSP数据划分算法对数据进行预处理，使得各数据对象均匀的划分到各个运行节点（DataNode）上；然后基于DBSCAN 密度聚类对数据块中数据进行聚类后剪枝优化，得到小规模的初始离群数据集；最后计算其局部离群因子［8］（LOF）来确定离群检测结果，从而提高算法的运行效率和准确率。

2 相关理论

2.1 密度聚类算法DBSCAN

DBSCAN 算法是基于一组邻域参数（ϵ，MinPts）来描述样本分布的紧密程度的一种算法。给定数据集D={x1，x2，…，xm} ，包含m 个样本，每个样本xi=(xi1;xi2;…;xin)是一个n 维特征向量，其中m，n，i为正整数，定义如下概念［10～11］。

定义1ϵ-邻域：对xj∈D，其ϵ-邻域包含样本集D 中与xj的距离不大于ϵ的样本，即Nϵ(xj)={xi∈D|dist(xi，xj)≤ϵ}，其中j为正整数；

定义2 核心对象：若xj的ϵ-邻域至少包含MinPts个样本，即|Nϵ(xj)|≥MinPts，则xj是一个核心对象；

定义3 密度直达：若xj位于xi的ϵ-邻域中，且xi是核心对象，则称xj由xi密度直达；

定义4 密度可达：对xj与xi，若存在样本序列p1，p2，…，pn，其中p1=xi，pn=xj且pi+1由pi密度直达，则称xj由xi密度可达；

定义5 密度相连：对xj与xi，若存在xk使得xj与xi均由xk密度可达，则称xj与xi密度相连；

定义6 簇：由密度可达关系导出的最大的密度相连样本集合，即给定领域参数（ϵ，MinPts），簇C∈D是满足以下性质的非空子集：

1）连接性：xi∈C，xj∈C⇒xj与xi密度相连；

2）最大性：xi∈C，xj由xi密度可达⇒xj∈C。

综上所述，若xi为核心对象，由xi密度可达的所有样本组成的集合记为X(i)={xj∈D|xj由xi密度可达}为满足连接性与最大性的簇。以图1 为例，给出了上述概念的直观显示。其中：MinPts=3，虚线表示ϵ-邻域，x1是核心对象，x2由x1密度直达，x3由x1密度可达，x3与x4密度相连。

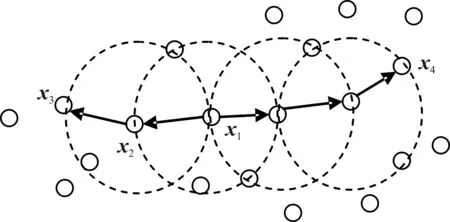
图1 DBSCAN定义的基本概念

其中对任意两个样本点xi和xj有：xi=(xi1，xi2，…，xin)和xj=(xj1，xj2，…，xjn)。xi和xj是n维属性空间的两个样本点且xi≠xj，它们之间的距离（欧氏距离）计算定义如下：

通常距离的计算还有以下几种：曼哈顿距离、闵可夫斯基距离、内积距离、余弦距离等，当数据对象的不同属性的重要性不同时，还可使用加权距离，利用权重ωi表征不同属性的重要性。聚类结束后生成的簇划分C={C1，C2，…，Ck}，定义：

定义7 簇Cl的中心点，其中l为正整数，|Cl|为簇Cl的样本数：

定义8 簇Cl内样本间的平均距离：

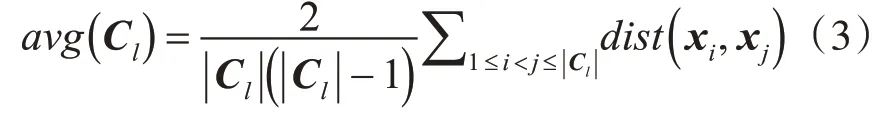
定义9 簇Cl内样本间的最远距离：

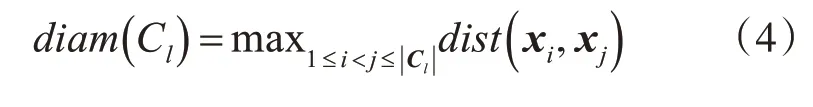
定义6簇Cl与簇Cm最近样本间的距离：

定义10 簇Cl与簇Cm中心点间的距离：

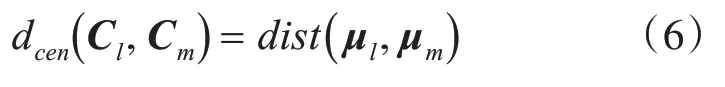
2.2 局部离群点检测算法LOF

通常情况下，离群点分为全局离群点和局部离群点两种类型，基于统计和基于距离的离群点检测算法适用于全局离群点的检测。通过对基于距离的检测方法的改进，Breunig 提出了基于密度的离群检测方法［8］，该方法提出基于密度的局部离群因子（LOF）概念作为离群度量，很好地解决了局部离群点的检测问题。对于任意样本点y且y∈D，算法的几个定义如下［12］：

定义11y的k-距离：数据集中到数据样本对象y距离最近的第k 个点到y的距离，记作k(y)其中k为自然数，这里的距离指欧式距离。

定义12y的k距离邻域Nk(y)：数据集中与与数据样本对象y的距离不大于k(y)的数据点组成的集合。

定义13y相对于s（s∈D且s≠y）的可达距离：

如果样本y远离样本s，则其可达距离就是它们之间的实际距离，如果二者足够近，则可达距离为y的k-距离。

定义14y的局部可达密度：

如果y是局部离群点的程度越小，则LOFk(y)值接近于1，即y不是局部离群点。相反，若y是局部离群点的程度越大，所得的LOFk(y)值越高。

2.3 分布式平台理论

Hadoop平台主要由MapReduce、HDFS、HBase、Hive 等项目组成。其中MapReduce 用于大规模数据集（大于1TB）的并行运算，其核心理念是将一个大的运算任务分解到集群每个节点上，充分运用集群资源，缩短运行时间［16］；HDFS是一个分布式文件系统，它通过将一个大的文件划分成一个个固定大小Block 来实现分布式存储［17］，目前HBase 的所有底层数据都以文件的形式交由HDFS 来存储；HBase 是一个分布式、按列存储的数据库［6］。其结构是以key-value 作为一行数据，可以随机访问、实时读取，对表中未存在的列和列簇不做存储，既节省空间，同时提高读写效率。本文在算法实现的机制中采用Hbase数据库和MapReduce模型。

MapReduce 模型分为Map 任务和Reduce 任务两个阶段。每一个MapReduce 作业执行时都会拆分成Map 和Reduce 两个阶段：Map 对应输入值key，value经处理后生成中间输出值key′，value′并作为Reduce 阶段的输入值，Reduce 对相同key'下的所有value'进行处理最后生成key′，value′ 作为最终结果。其流程如图2。

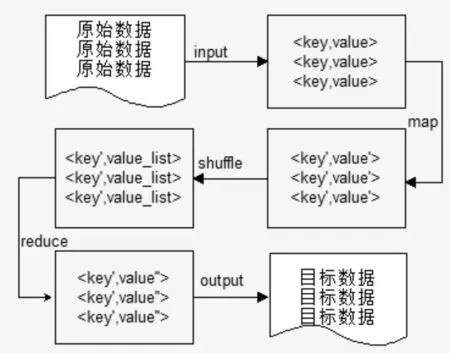
图2 MapReduce流程

3 本文算法

典型的基于密度的LOF 算法的核心思想是为每个数据对象赋予了表征其离群程度的离群因子，然后计算每个对象的离群度，并根据离群度排序，最后取其前若干个点作为离群点。相关的改进算法大多都是从距离度量方面以及最终离群因子的计算方面改进［4］。本文针对数据集的规模和距离度量方面借鉴前人的算法进行改进，在数据预处理阶段通过文献［5］DBSP算法将数据均匀划分后，利用DBSCAN聚类算法将大多数正常数据对象去除，从而削减数据集的规模，生成初始离群数据集，为保证数据集的整体特性不变，对LOF算法进行了相应的改进，最终找出离群点的集合。

3.1 基于密度聚类的离群点检测算法

3.1.1 基于DBSCAN算法的数据预处理

Hadoop 分布式系统对数据集随机分块，这一过程对离群点检测的准确率存在一定的误差，为了减小这一误差，采用文献［5］DBSP数据划分算法对数据进行预处理，使得数据能均匀的划分到各个数据块中。DBSCAN 算法的时间复杂度为O(nlogn)相对较低，能够处理任何大小和形状的簇。所以利用DBSCAN 算法来对海量的复杂数据集进行剪枝处理是很好的。DBSCAN算法具体算法描述下：

输入：数据集D，邻域参数（ϵ，MinPts）

输出：簇划分C={C1，C2，…，Ck}的中心点，包括各簇的平均距离、最大距离。

算法过程：

1）确定邻域参数（ϵ，MinPts），根据式（1），定义1确定数据对象xj的ϵ-邻域Nϵ(xj)；

2）如果|Nϵ(xj)|≥MinPts那么将样本xj加入核心对象集合：O=O∪{xj} ；

3）随机选取一个核心对象o∈O，找出所有从该点密度可达的对象，形成一个类簇；

4）重复步骤2）、3）直到形成聚类簇划分C={C1，C2，…，Ck}；

5）利用式（3）、式（4）分别计算各簇Cl的平均距离avg(Cl)，最大距离diam(Cl)；

6）利用式（2）分别计算各簇的中心点μ={μ1，μ2，…，μk} 保留中心点作为各簇的代表；

7）输出：初步离群数据集D′=DC∪μ。

3.1.2 改进的LOF算法实现

数据集D经过数据预处理之后，剪掉大部分正常的数据对象，缩小了数据集的容量，形成初步离群数据集D′。为了确保数据的分布特性，提高算法的准确率，数据集D′中保留了聚类后各簇的中心点。由离群点的定义可知，类簇内的点不会是离群点，所以为了避免这些中心点被选为离群点，对LOF算法计算可达距离时进行了适当的改进，取权值ω=0.618 为中心点加权，使之不可能成为离群点。具体改进后的算法描述如下：

输入：d维数据集D′，k，离群因子阈值ξ

输出：离群点集合E

算法过程：

1）计算任意对象y（y∈D′）的k-距离k(y)并找出y的距离邻域Nk(y)

2）计算y相对于s（s∈D且s≠y）的可达距离，其中对象y，s要分类讨论来调整可达距离。

（1）若对象y，s都不是中心点，则可达距离由式（7）计算出reach_dist(y，s)；

（2）若对象y，s均是簇Cl和Cm的中心点，则可达距离为

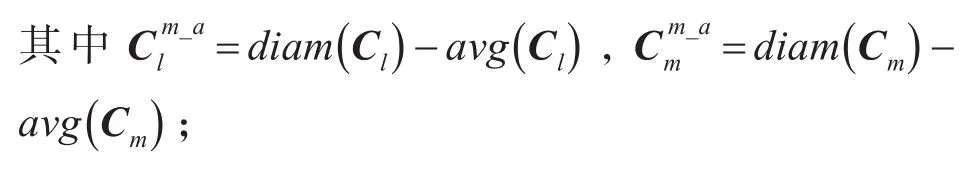
（3）若对象y，s只有一个是簇Cl的中心点，则可达距离为

3）利用式（8）和步骤2）的改进计算各对象的局部可达密度。

4）利用式（9）计算各对象的局部离群因子。

5）若某个对象的离群因子LOF 值大于给定的阈值ξ，则输出。

3.2 基于密度聚类的离群点检测算法并行化

Hadoop 支持多种方式作为数据输入源，本文采用HBase作为分布式数据库，存储数据源。算法步骤如下：

第1 步输入原始数据集D，使用DBSP 算法确定数据集的均匀划分，将数据块存入DataNode 节点中。

第2 步由步骤1 产生的数据块构建键值对K，V，K值表示所取的行号，V表示此行的字符串内容。Map 阶段不做处理，在Reduce 阶段将数据过滤，提取属性值，输出id，property，id值表示数据对象xi的唯一标识id，property表示数据对象xi的各个属性值{xi1;xi2;…;xin} ，并存入输出文件中。

第3 步输入第2 步处理过的键值对id，property，在Map 阶段不作处理，在Reduce 阶段根据式（1）计算所有对象xi与其他对象的距离dist(xi，xj)，输出键值对id，dist，dist中表示xi的与其他对象的距离dist(xi，xj)值，并存入输出文件中。

第4 步输入第3 步产生的键值对id，dist，Map 阶段不作处理，在Reduce 阶段计算出xi的ϵ-邻域，输出键值对id，neighbor，其中neighbor表示每个数据对象xi的ϵ-邻域Nϵ(xi)。

第5 步输入第4 步产生的id，neighbor，Map阶段根据根据3.1.1 节算法过程（1）～（2）确定核心对象集O，在Reduce 阶段根据3.1.1 节算法过程（3）～（4）确 定 簇 划 分C={C1，C2，…，Ck} ，输 出

d，object，其中d 表示簇类号，object表示簇中对象，

第6 步输入第5 步产生的键值对d，object，Map 阶段融合第2 步产生的键值对，根据3.1.1 节算法过程5）利用式（3）、式（4）分别计算各簇Cl的平均距离avg(Cl)，最大距离diam(Cl)，在Reduce 阶段根据3.1.1节算法过程6）～7）根据式（2）找出各簇的中心点μ={μ1，μ2，…，μk} ，确定初步离群数据集D′=DC∪μ，输出D′_id，C_core。其中，D′_id表示初步离群数据对象id，C_core表示是否是簇的中心点、簇的平均距离和最大距离，并存入输出文件中。

第 7 步输入第 6 步产生的键值对D′_id，C_core，Map 阶 段 融 合 第3 步 产 生 的id，dist，根据3.2.2 节算法过程1）产生各对象的距离邻域，在Reduce 阶段根据3.2.2 节算法过程2）计算各对象的可达距离，输出D′_id，reach其中D′_id表示每个数据对象的id，reach表示对象的可达距离。

第 8 步输入第 7 步产生的键值对D′_id，reach，在Map 阶段根据3.2.2 节算法过程3）计算各对象的局部可达密度，在Reduce 阶段根据3.2.2 节算法过程4）计算各对象的局部离群因子，输出键值对D′_id，lof，其中lof表示数据对象的局部离群因子。

第9 步输入第8 步产生的键值对D′_id，lof，在Map阶段不作处理。在Reduce阶段根据3.2.2节算法过程5），找出离群对象，输出键值对Outlier_id，Outlier_lof，其中Outlier_id表示离群对象的id，Outlier_lof表示离群对象的离群因子。

4 实验结果与分析

本文实验所采用硬件环境：内存4.00GB，处理器Intel（R）Core（TM）i5-4590 CPU @ 3.30GHz 3.30 GHz。软件环境：四台机器安装CentOS7.0 操作系统，Hadoop 生态环境采用Hadoop-2.6.0，HBase-1.0.1.1，Zookeeper-3.4.6，JDK-1.8.0_25，集成开发环境采用Eclipse。

实验所用数据为网络入侵检测数据集KDD-CUP1999 数据集，该数据集中的数据对象分为5 大类，包括正常的连接、各种入侵和攻击等。KDD99 数据集总共由500 万条记录构成，共41 维属性，该数据集提供了一个10%的训练子集和测试子集，为了进行实验，对非数值属性维进行数值化处理。随机抽取4类异常类型数据30万条，并加入正常数据10、20、30、40 条作为离群数据，进行算法验证，并与传统的LOF算法，文献［4］提出的算法和本文提出的GJLOF 算法进行比较。检测结果如表1所示。

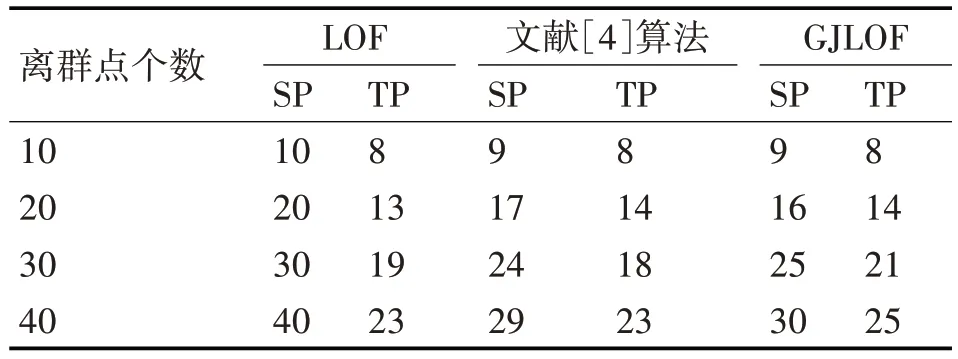
表1 各算法检测结果

其中SP：检测出的总数，TP：检测出正确的个数。

1）使用离群点检测精度衡量算法性能

图3 各算法精确度比较

2）使用计算时间复杂度衡量算法性能

本节实验用于评估本文算法的时间性能。分别从KDD99 数据集中选取不同规模的数据作为实验数据集，然后在这些数据集上分别运行LOF、文献［4］提出的算法和本文算法GJLOF。图4 给出了实验结果。随着数据规模的不断增加，本文算法的运行时间更低；相同数据规模下，本文算法运行时间相对较少。

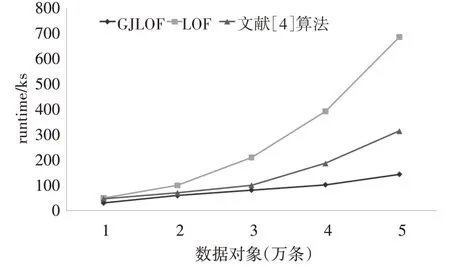
图4 各算法运行时间比较

3）数据可扩展性实验

随着数据规模的不断增加，对于分布式系统来说，数据节点的数量同样影响算法的运行效率。采用相同的实验环境，依照节点的数量不同启动1～3台DataNode 节点机，并将数据集KDD99 处理加工成1Million、5Million、10Million 三种规模的数据进行实验，对不同规模的数据都重复实验三次，取平均值作为最终结果。由于硬件和网络环境会造成Hadoop 集群节点的运算和通信差别，因此采用运行时间比R=t1作为指标量，其中t1为集群节点数量为1 的运行时间，n 为集群节点数。具体结果如图5。

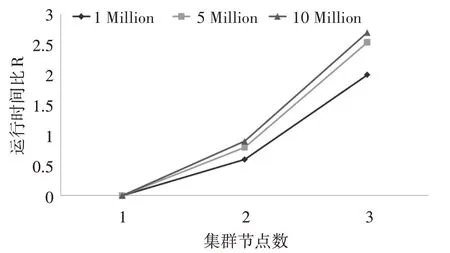
图5 集群运行时间

根据图5 的实验结果可以看出，随着集群节点的增多，相同规模数据集的计算效率有所提高，并且不同规模的数据集，数据规模越大，节点数量的变化对计算效率越明显。

5 结语

本文提出了一种基于密度聚类的分布式离群点检测算法，算法首先采用密度聚类算法，实现对数据规模的约简，然后根据计算出的局部可达密度和局部离群因子，最终找出离群点。从实现机制上采用Hadoop 平台上的MapReduce 模型框架，以HBase 作为数据库，解决了算法的数据规模过大的问题。本文算法通过对数据集规模上的约简，解决了离群点检测算法计算量较大的问题，运行效率明显提高，通过改进LOF 算法的可达距离，提高了准确率，但是由于对数据进行并行化操作时导致数据集聚类效果受到影响，并且算法对参数（ϵ，MinPts）和k距离参数比较敏感，未来可以在解决数据均匀划分和参数问题上进行研究。