一种改进的电动汽车锂电池RC滞后模型及其应用＊

孙川 褚端峰 李海波 王建宇

（1.黄冈师范学院，黄冈 438000；2.武汉理工大学，智能交通系统研究中心，武汉 430063；3.东风汽车公司技术中心，武汉 430056）

主题词：电动汽车 荷电状态 一阶RC滞后模型 自适应粒子滤波

1 前言

动力电池的成本、能量密度、循环寿命等是制约电动汽车发展的关键因素。解决这一问题，可以从两个角度出发：一是开发成本低、能量密度高、循环寿命长的电池；二是开发有效的电池管理系统，通过科学管理充分发挥其性能优势[1]。荷电状态（State Of Charge，SOC）估计是电池管理的重要内容，研究电动汽车SOC估计问题，对于电池科学管理、合理安排充电时机具有现实意义。

电池SOC估计方法可以分为3类：传统方法，包括开路电压法[2]、内阻法[3]、安时积分法[4]等；基于黑箱模型的估计方法，包括神经网络模型[5]、模糊逻辑模型和支持向量回归模型[6]等；基于状态空间模型的估计方法，常用方法有卡尔曼滤波[7]、粒子滤波[8]、H∞算法等。其中，传统方法不适宜在电池使用时进行估计，基于黑箱模型的估计方法对试验数据的数量和准确性依赖较强，基于状态空间模型的估计方法是当前研究的重点。粒子滤波的各种自适应改进及应用也被广泛研究：Li[9]提出了粒子数随时间自适应变化的粒子滤波方法，此方法以相对熵（Kullback-Leibler Divergence）为依据确定下一时刻粒子数，实现了计算量减小的目的；Zuo等[10]提出了重要密度函数自适应更新的粒子滤波方法，解决了采样效率低的问题，提高了算法估计精度；Straka等[11]依据估计误差调整粒子数量，将估计误差控制在一定范围内，同时致力于减少计算量。

以上粒子滤波的自适应改进方法是算法自身的改进，本文结合电池SOC估计问题，充分利用已辨识的模型信息，以模型估计值与观测值之差为依据，自适应调整模型的状态噪声和观测噪声，达到了提高电池SOC估计精度、速度和鲁棒性的目的。

2 锂电池模型及参数辨识

2.1 锂电池模型

本文使用等效电路模型对锂电池进行建模。等效电路中有3个常见模块：

a.欧姆内阻模块。内阻R0由电极材料、隔膜电阻、电解液对电荷的运动阻力产生。

b.RC网络模块。电池使用时具有极化现象，本文使用极化电容Cp与极化电阻Rp组成的RC网络模拟这一过程。对电池建模时，通常使用RC网络串联提高模型精确度。但4阶及以上的RC网络会大幅增加计算量，而模型精度提高很小，故一般使用3阶及以下的RC网络。第i个RC网络端电压与电阻、电容的关系为：

式中，Δt为采样周期；τi=RiCi为时间常数；Upi,k为k时刻第i个RC网络的端电压；Rp为极化电阻；Ik为k时刻RC网络电流。

c.滞后模块。滞后模块用于反映电池电压变化相对于电流变化的延迟现象。美国的Plett教授给出了滞后模块的公式[12]：

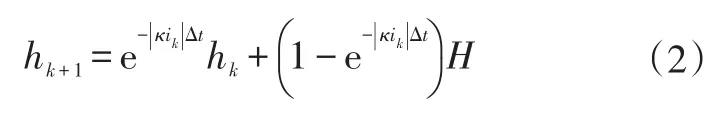
式中，hk为k时刻滞后电压；κ为衰减因子；ik为k时刻电流；H为最大滞后电压。

使用上述模块，本文分别建立了1阶、2阶、3阶RC及RC滞后模型共6个模型，图1给出了1阶RC及RC滞后模型，2阶与2阶以上模型在1阶模型基础上串联相应数量的RC网络。

1阶RC模型方程为：

式中，Ut,k为k时刻电池输出电压值；zk为k时刻电池SOC值；Uocv为开路电压。

为了保证拟合精度，本文使用n次多项式拟合Uocv～z关系式，即

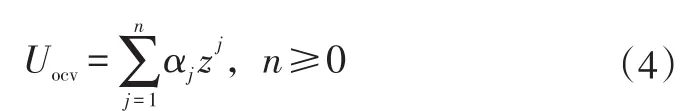
式中，αj为拟合系数。

1阶RC滞后模型方程为：

2阶RC模型和RC滞后模型方程分别为：

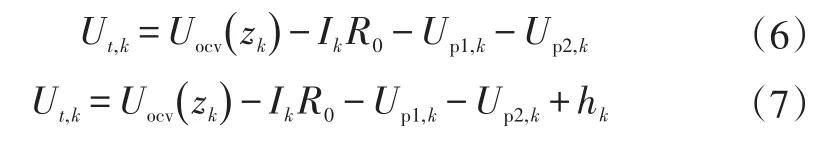
3阶RC模型和RC滞后模型方程分别为：

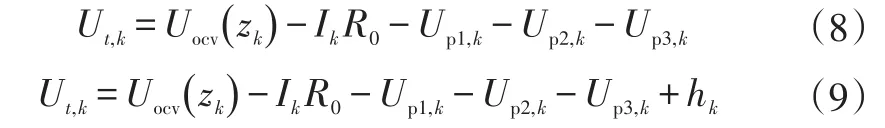
图1 1阶RC及RC滞后模型

2.2 模型参数辨识

首先使用试验法和多项式拟合对式（4）进行辨识，试验要求在25℃恒温条件下进行，电池充满电后静置2 h使其状态稳定，然后放电5min，释放电量为1 C，再次静置5min用于稳定状态，记录静置期间的最大开路电压作为此SOC下的开路电压。重复以上步骤直至放电完毕，得到不同SOC值下的试验数据，使用多项式拟合得Uocv～zk关系式为：

对于1阶、2阶、3阶RC及RC滞后模型，首先进行混合动力脉冲能力特性（Hybrid Pulse Power Characteristic，HPPC）测试，而后使用粒子群算法[13]搜索最优解，以模型端电压误差的均方根为适应函数，综合考虑模型误差与计算量选择锂电池的等效模型。参数辨识以SOC每10%为一个区间，HPPC测试数据如图2所示。

图2 锂电池HPPC测试数据

在粒子群算法中，粒子速度的更新受自身速度、自身历史最优位置、种群最优位置的影响，向自身历史最优位置和种群最优位置靠拢。使用粒子群优化算法搜索各模型的最优参数，结果如图3所示。

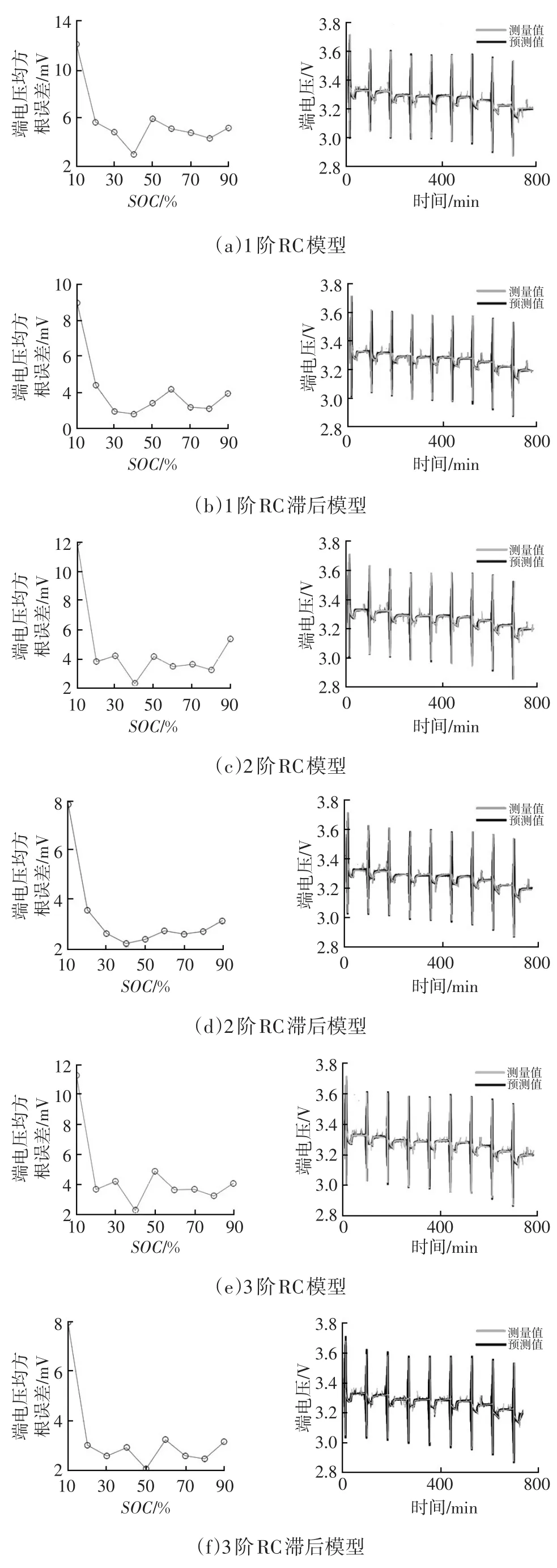
图3 各模型参数优化结果

通过计算端电压误差均方根的平均值，可以看出模型精度最高的是3阶RC滞后模型，其次为1阶RC滞后模型，两者平均值相差约0.8mV，综合考虑模型精度和计算量，本文选择1阶RC滞后模型作为锂电池模型。

2.3 锂电池空间模型

依据式（5）的1阶RC滞后模型和式（4）给出的Uocv～z模型，选择状态向量x k=(Up1,k,hk,zk)T，将锂电池等效电路模型和开路电压方程离散化，得到状态转移方程和观测方程分别为：

式中，Ca为电池可用容量；η≈1为库伦系数；o k、vk分别为过程噪声和观测噪声。

分析式（11）可知，R0、Up1,k、hk经过参数辨识过程已知，Ik、Ut,k可以实时测量，通过粒子滤波方法调整vk，使Uocv(zk)更加准确，即可根据式（10）计算出SOC。

3 自适应粒子滤波

3.1 传统粒子滤波分析

由式（11）可以看出，锂电池空间模型为非线性模型。传统的卡尔曼滤波无法应用于非线性系统，扩展卡尔曼滤波又会带来较大的非线性误差，因此本文选用粒子滤波方法。粒子滤波实质是利用后验概率分布对变量进行估计。

粒子滤波已经非常成熟，算法原理可参考文献[14]、文献[15]，在此简要分析。记某一非线性空间方程为：

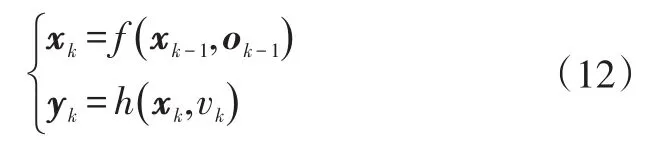
式中，x k、y k分别为k时刻的状态向量和观测量；f()、h()均为已知函数。

记系统状态的后验分布为p(x k|y k)，但其不具有标准形式，难以采样。使用重要性采样方法，引入容易采样的概率分布q(x k|y k)，要求q(x k|y k)也定义在状态空间中，取值范围大于p(x k|y k)。q(x k|y k)被称为重要性函数，在重要性函数下采集N个样本，得到样本集。

将重要性函数引入后验分布中，得

式中，ξ为狄拉克函数；为归一化后k时刻第i个样本的权值，且

为了实现滤波过程的递推计算，将重要性函数变形，并结合贝叶斯估计理论，可得

算法经过若干次迭代后，会出现粒子退化现象，也就是权重大的粒子会保持优势，甚至越来越大，其他大量粒子权重越来越小，不仅产生了无用计算，而且估计精度也会降低。为解决这一问题，需要进行粒子重新采样。

本文使用有效样本数Neff评价粒子退化程度，作为粒子是否需要重新采样的依据：

式中，var()为方差函数；N为实际粒子数。

对有效样本数设置一个阈值Nth，若Neff≤Nth则说明粒子退化严重，需要重新采样。

本文使用随机重采样方法进行重新采样。首先对归一化权值进行累加，得；其次在[0,1]上产生N个随机数{uj}(j=1,…N)；搜索使cl≥uj成立的最小l，使新粒子，同时定义每个粒子权重为1/N，即可实现粒子重采样。

3.2 自适应粒子滤波提出

现有的自适应粒子滤波方法是对状态噪声的自适应调整：

式中，λ为平滑滤波窗口；σc,k为自适应调整后的状态噪声；c为状态向量的某一状态变量；β∈[0.1,1]为衰减因子；σc,min为状态c的最小噪声方差；σc,mid为中等噪声方差。

本文在此自适应粒子滤波基础上进行改进，对观测噪声也进行自适应调整。改进思路为：建立等效模型时确定模型的误差范围，将状态估计值代入观测方程后得到观测估计值，则观测值的估计误差也应在一定范围内，如果观测值误差与模型误差偏差较大，则需要较大的观测噪声方差使算法快速收敛。

3.2.1 确定观测误差边界

观测误差可认为服从正态分布，记第i个粒子的实测值为，模型估计值为，实测值与估计值误差为，误差平均值记为μ，标准差记为δ，则

式中，w为辨识区间的数据个数。

根据大数定律，当w足够大时，观测误差的均值和方程可以使用μ和σ2近似代替，根据参数的区间估计原理，取置信度为95%，得到观测误差边界为，其中Ua为标准正态分布的上分位数。

3.2.2 观测误差自适应调整

将状态估计值代入观测方程，得到的观测估计值误差可能来源包括状态噪声、观测噪声、初值误差等。一般来讲，状态噪声和观测噪声在一定范围内，而初值误差等其他干扰可能引起较大误差，参考上文中设定的观测误差边界，本文观测噪声自适应调整为：

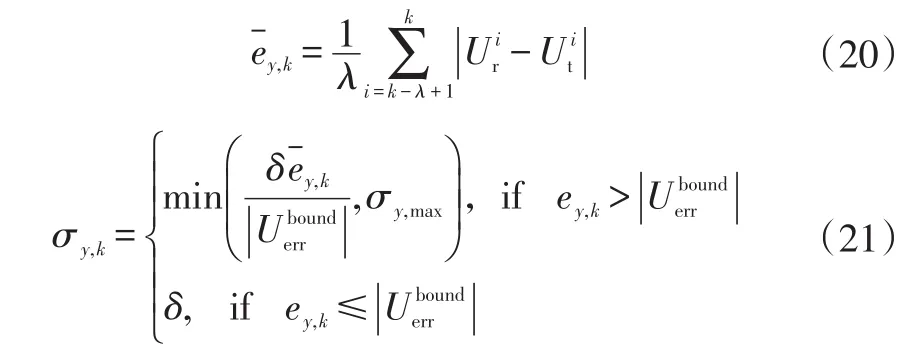
式中，ey,k为观测误差估计值；σy,k是自适应调整后的观测误差标准差；σy,max为观测量的最大噪声标准差差设定值。

式（20）和式（21）使用误差平均值作为判断标准，是为了防止抖动的干扰。

3.3 基于自适应粒子滤波的SOC估计

本文基于电池1阶RC滞后模型的状态空间方程和自适应粒子滤波方法，给出电池SOC估计流程如图4所示。其中，初始化参数包括粒子、粒子权重、初始化噪声方差、有效阈值、SOC、极化电压、滞后电压、粒子数等，粒子权值的计算公式为，k时刻状态估计值为。

图4 SOC估计算法流程

4 仿真验证

4.1 收敛速度验证

本次仿真中，SOC初始真值设置为0.80，SOC估计值设置为0.50，即初始误差到达了0.30，分别使用传统粒子滤波方法和本文提出的自适应粒子滤波方法进行SOC值估计，如图5所示。

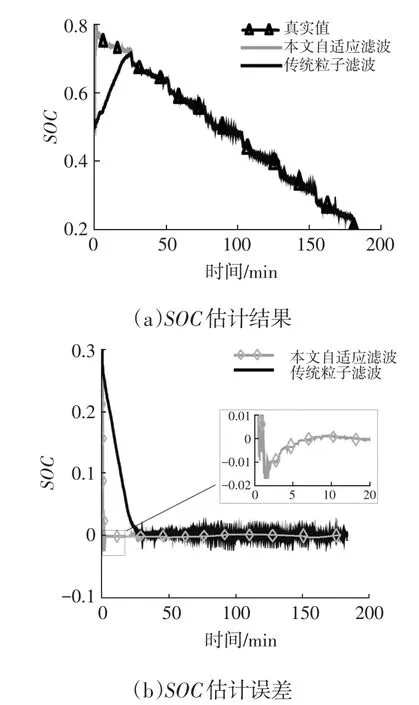
图5 两种算法的SOC估计结果

由图5可以看出，在电池SOC初始误差较大情况下，本文提出的自适应粒子滤波在第30 s左右收敛到了真实值附近，而传统粒子滤波在24min后才收敛到真实值附近，说明本文提出的自适应粒子滤波在收敛速度和鲁棒性方面具有明显优势。这是因为本文提出的自适应滤波在现有自适应算法基础上，通过观测误差值与设定误差边界比较，实现了观测噪声依据观测误差的自适应调整。

4.2 收敛精度验证

为了验证本文提出算法的SOC估计精度，将SOC的估计区间设置为0.80～0.20，SOC初始值设置为0.70，即存在0.10的初始误差。分别使用传统粒子滤波与本文提出的自适应粒子滤波对SOC进行估计，得到的估计值和估计误差如图6所示。

图6 两种算法对SOC估计结果

为了更加精确地对比两种算法的估计精度，表1给出了两种算法对SOC估计的统计数据。

表1 两种算法的SOC估计统计数据

由图6和表1可以看出：两种算法对SOC估计精度都较高，均未超过3%，但自适应粒子滤波估计算法精度更高；自适应滤波的估计误差比传统方法更加稳定；从收敛时间上看，自适应算法极大地提高了收敛速度。自适应算法在收敛精度、收敛速度上的优势，源于自适应算法对状态噪声和观测噪声的自适应调整，使状态噪声和观测噪声能够适应环境和其他因素引起的误差变化。

5 结束语

本文建立了电池的1阶RC滞后模型，提出了自适应粒子滤波算法，仿真结果表明：在初始误差较大时，本文提出的自适应滤波算法具有很快的收敛速度和很好的鲁棒性；与传统粒子滤波相比，本文提出的自适应算法收敛精度高、收敛稳定性好、收敛速度快。这说明通过观测误差自适应调整观测噪声，使其对各种因素引起的误差具有自适应性，可以提高算法的估计速度和精度。