一类三阶非线性系统的全局渐近稳定性
2019-07-09 10:40:02徐静
陕西理工大学学报(自然科学版) 2019年3期
徐 静
(安徽师范大学 数学与统计学院, 安徽 芜湖 241000)
非线性微分系统平衡位置的稳定性在现代物理、工程技术和生态系统等领域有着重要意义,处理非线性微分系统稳定性这一问题的重要方法之一就是Liapunov直接方法(类比法),这一方法一直吸引着众多学者们的关注与兴趣,并得到了极为广泛的应用,三阶及以下的非线性系统的平凡解的全局稳定性也取得丰硕结果[1-8]。本文在文献[1-5]的基础上研究了多个三阶非线性系统的Liapunov函数,并得到了各自零解全局渐近稳定性的若干充分条件。
1 主要结果
考虑系统

(1)
约定函数h(0)=0,f(0)=0,φ(0)=0,f(x)、g(x)、φ(x)是连续可微的,且能保证系统解的唯一性。
退化为线性系统
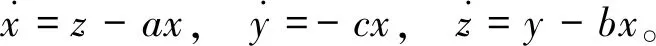
对其退化线性系统取Liapunov函数V1=V1(x,y,z)如下:
由类比法给出系统

取其Liapunov函数V2=V2(x,y,z)如下:
(2)
对于系统

(3)
其退化系统取Liapunov函数V=V(x,y,z)如下:
由类比法给出系统(3)Liapunov函数V3=V3(x,y,z)如下:



(4)
结合式(2)和(4),系统(1)有Liapunov函数:

(5)
于是得到如下结果:


(*)
由定理假设并注意到:
故V(x,y,z)为正定函数,

下证系统(1)的所有正半轨线是有界的。取如此大的正数l和N使得任一点P0位于由不等式V(x,y,z)
事实上,由式(*)知在D中当y≠0时有
(**)

2 讨 论


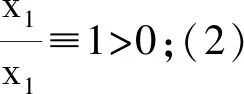




这里取b=1/A>0,推论3结论成立。
猜你喜欢
数学年刊A辑(中文版)(2023年4期)2024-01-04 05:47:40
力学学报(2022年12期)2023-01-15 12:32:46
数学物理学报(2022年2期)2022-04-26 14:08:16
湖北工程学院学报(2021年3期)2021-06-16 01:25:48
宜宾学院学报(2020年12期)2021-01-30 06:07:20
数学物理学报(2019年6期)2020-01-13 06:08:24
数学物理学报(2019年3期)2019-07-23 01:15:30
福建中学数学(2016年4期)2016-10-19 05:09:02
山西大同大学学报(自然科学版)(2016年6期)2016-01-30 08:29:10
国外科技新书评介(2014年12期)2015-01-05 17:27:05

