基于MEMD和RVM的滚动轴承外圈故障评判

张雨琦， 邹金慧*

(1.昆明理工大学 信息工程与自动化学院， 云南 昆明 650500；2.云南省矿物管道输送工程技术研究中心， 云南 昆明 650500)

滚动轴承作为旋转机械中最为常用的机械零件，其运行状态对于保障机械设备安全运行，避免重大事故具有重要意义。一旦轴承出现故障或失效，就会直接影响到整个机械系统的正常运转。因此，为了避免这种情况的出现，需对滚动轴承外圈故障进行评判，以便保证机械设备的正常运转。

滚动轴承工作过程中，其外圈处于固定状态，故障点位置是固定不变的，基于此，故障点的位置是否在轴承的承载区，对机械设备的正常运行造成直接影响。为了全面分析滚动轴承的运行状况，采用多通道分析的方法对轴承外圈故障信号进行处理。传统的经验模态分解(Empirical Mode Decomposition，EMD)方法在处理多通道信号时，存在分解的固有模态函数(Intrinsic Mode Function，IMF)分量个数不一致和模态混叠的问题[1-2]，而Rehman等[3]提出的多元经验模态分解(Multivariate Empirical Mode Decomposition，MEMD)则可以自适应地将多通道信号分解为具有相同个数的多元本征模函数(Multivariate Intrinsic Mode Function，MIMF)分量。考虑到在相同频率尺度上，不同通道的特征波形之间存在对应关系，因此能够据此得到通道间多尺度特征模式信息，达到均衡采样的目的。将此方法与全矢谱、极限学习机等方法相结合[4-5]，在飞机故障健康状态预测或轴承故障特征提取等领域取得了较好的应用效果。

熵值是一种表征信号复杂程度的指标[6]，因其抗噪能力强、处理数据长度要求不高等特点而被广泛应用于脑电、心电、机械故障诊断等领域。互近似熵是近似熵的改进算法[7]，它能更加准确地描述时间序列的不规则性和复杂度，利用互近似熵指标来量化故障信号各频带内的复杂度等特征，能够更加直观地掌握设备的运行状况[8]，因此，本文引入互近似熵来表征滚动轴承的故障特征。

2001年，美国学者Tipping[9]充分结合支持向量机(Support Vector Machine，SVM)和稀疏贝叶斯统计理论，创造了全新的学习方法——相关向量机(Relevance Vector Machine，RVM)，该方法应用的训练模式是在贝叶斯框架下完成的。RVM与SVM在函数形式上相似，但RVM在参数设置、核函数选择以及输出形式等方面更具优势[10-11]，因此RVM能够实现更高的分类效率，节省了分类时间。

本文采用MEMD的多通道分解法对滚动轴承外圈分别分布在3点钟、6点钟、12点钟3个不同方位的传感器所采集的振动信号进行分解，提取有效分量，结合互近似熵指标和RVM分类器的分类优势，将提取的故障特征值构建特征向量，输入RVM分类器进行故障方向的分类评判。

1 多元经验模态分解

MEMD算法以EMD算法为基础，具备更好的自适应性，能对多通道信号进行分析[12-13]，其分解步骤如下：

步骤2：确定方向向量集V，获取原始信号即z(t)在k个方向上的向量vk(k=1,2,…,l)上的投影集，设为pk(t)，其中l为方向向量个数。

步骤4：取D(t)=X(t)-C(t)，对D(t)进行判断，若D(t)满足MIMF的迭代终止条件，则定义其为MIMF1，若不满足则重复步骤2和步骤3，直到满足MIMF终止条件为止。

2 互近似熵

以N点时间序列{x(k)}为对象展开相空间重构，获取若干m维矢量y(i)，i=1,2,…,n-m+1，取如下两个矢量[7]：

Yi=y(i)y(i+1)…y(i+m-1)，

(1)

Yj=y(j)y(j+1)…y(j+m-1)，

(2)

其中j=1,2,…,n-m+1且i≠j。

定义上述矢量Yi与Yj间相应元素的最大差值为两矢量的距离：

(3)

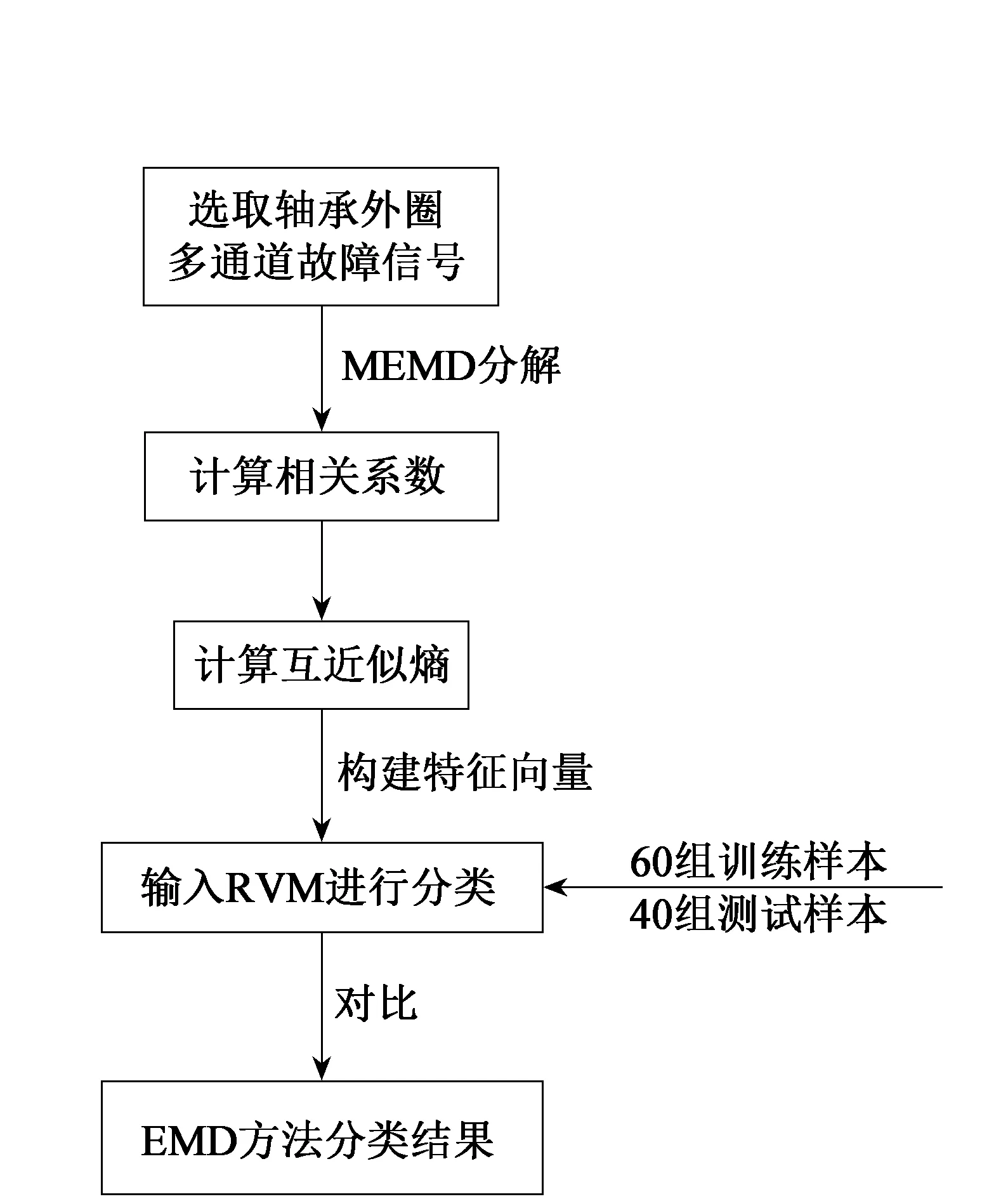
按照已经设定的相似容限度r(r>0)，对所有i、j统计D(y(i),y(j))

Θm,r(y(i),y(j))=Nm,r/(n-m+1)。

(4)

定义矢量Yi与Yj之间的互相关程度为

(5)

如果Yi与Yj的嵌入维数是m+1，通过计算确定二者的互关联程度Ωm+1,r(y(i),y(j))，据此确定时间序列的互近似熵为

S=Ωm,r(y(i),y(j))-Ωm+1,r(y(i),y(j))。

(6)

3 相关向量机

(7)

其中w=[w0,w1,…,wN]T，K(x,xi)代表核函数。

整个数据集的似然函数为

(8)

式中σ[y(xi,w)]为sigmoid函数。

为避免过拟合，保证RVM分类模型的稀疏性，对w赋予零均值高斯先验分布：

(9)

新的输入向量x*，其目标值t*的概率预测式为

(10)

由贝叶斯推导，可得

P(w,α,σ2|t)=p(w|t,α,σ2)P(α,σ2|t)，

(11)

对式(11)进行最大化处理，可得到α、σ2的迭代更新公式为

(12)

γi=1-αiΣi,i，

(13)

式中Σi,i为后验协方差矩阵Σ中第i项的对角线元素，μi为权重向量μ=σ-2ΣΦTt的第i个元素。

4 基于MEMD和RVM的滚动轴承外圈故障评判流程

图1 外圈故障评判流程图

如图1所示，利用MEMD分解与RVM相结合的方法进行滚动轴承外圈故障评判流程如下：

①选取滚动轴承外圈不同角度传感器采集的多通道故障信号，利用MEMD对其进行多尺度分解，分解为多个按频率尺度对齐的个数相同的MIMF分量。

②通过计算确定每个通道信号所分解的MIMF分量与其对应通道原信号的相关系数，选择相关系数最大的前两个MIMF分量作为有效分量进行后续分析。

③通过计算确定上一步骤中两个MIMF分量的互近似熵值，将得到的结果作为x、y坐标构成特征向量。

④基于构建的特征向量，建立RVM轴承外圈故障评判模型，完成所提方法有效性的实验验证。选取60组故障信号作为样本集，对RVM进行训练；另外随机抽取40组故障信号作为测试集，输入RVM进行分类。

⑤将RVM的评判结果与经EMD分解后的IMF分量的互近似熵值的分类结果进行对比，进一步论证本文所提方法的有效性。

图2 外圈故障信号时域波形图

5 工程应用

为了论证所提方法的有效性和可行性，利用美国凯斯西储大学轴承数据中心的轴承故障数据进行实验分析，实验装置由一个2 hp(1 hp=746 W)电机、转矩传感器、一个测力计和电子控制装置组成，加速度计固定在电机壳体外部，用来采集振动数据。故障是用电火花在轴承上加工而成的单点损伤，本文所选数据为分别位于3点钟、6点钟及12点钟位置的传感器所采集的轴承故障数据，故障直径均为0.007英寸(0.177 8 mm)。轴承参数如表1所示。

表1 轴承参数

首先，分别选取滚动轴承外圈位于3点钟、6点钟及12点钟方向的传感器所采集的多通道故障振动信号100组，每组1024个点作为实验样本进行实验分析。由于篇幅所限，仅展示3个方向的故障信号各一组实验样本的时域波形图，如图2所示。对实验样本进行MEMD分解和EMD分解，由于篇幅限制，只展示其中一组数据的分解结果，通道1为故障点位于3点钟方向的振动信号，通道2为故障点位于6点钟方向的振动信号，通道3为故障点位于12点钟方向的振动信号，分解结果如图3、图4所示。

图3 外圈三通道信号MEMD分解图

图4 外圈三通道信号EMD分解图

由图3、图4对比可知，多通道信号通过EMD分解得到个数不同、波形不齐的IMF分量，而通过MEMD分解法分解多通道信号则可得到一系列个数相同、波形对齐的MIMF分量。通过求取各个通道信号经MEMD分解后的MIMF分量的相关系数，提取与原信号相关系数高的MIMF分量进行研究，其相关系数图如图5所示。

由图5可知，前两个MIMF分量与原信号的相关系数最大，因此选择前两个经MEMD分解后的MIMF分量作为有效分量并求取互近似熵值。由于篇幅限制，表2列出前10组互近似熵值。分别将求取的MIMF1分量及MIMF2分量的互近似熵值作为x、y坐标，以构建互近似熵值特征向量。将60组特征向量输入RVM中进行训练，再随机抽取另外40组测试样本输入RVM中进行测试，测试结果如图6所示，其中圆圈标记的就是相关向量样本点。当相关向量点数量越少，则对分类结果造成影响的主要向量越少，对所有非相关向量的核函数无需再进行计算，节省分类时间的同时，也可以实现更高的计算效率。

接下来对新方法的效果进行验证，将新方法与经EMD分解后的互近似熵所构成的特征向量训练的RVM分类结果(图4所示)进行对比。通过分析图6的识别结果可知，图6(a)的识别率为92.5%，而图6(b)的识别率则为100%，由此可以判断出基于MEMD的互近似熵分类结果优于基于EMD的互近似熵分类结果，单一的信号分解对滚动轴承外圈故障信号的分析较为局限，而多通道信号同时分解则可最大程度地保证通道间的互信息，通过互近似熵的互信息性对轴承故障特征进行提取并输入分类器进行分类。实验结果表明：本文所选用的方法对于滚动轴承外圈故障信号的评判具有更高的优越性和可行性。

表2 外圈三通道故障信号的MIMF分量互近似熵值表

6 结 语

图5 外圈三通道故障信号相关系数图

本文结合MEMD和RVM分类方法，提出一种基于MEMD和RVM的滚动轴承外圈故障评判方法，对滚动轴承外圈3点钟方向、6点钟方向及12点钟方向的故障方位进行评判，通过实验得到以下结论：

(1)MEMD分解法可用于多通道滚动轴承故障信号的分解，能够最大程度地保证通道间的互信息，优于EMD分解法对于单一通道信号的分析。

(2)在故障信号经MEMD分解后引入能够定量化识别特征的互近似熵指标，可以实现对滚动轴承外圈3个角度的传感器所采集信号的量化评判。

(a) EMD (b) MEMD图6 RVM分类结果

(3)将经MEMD分解后提取的互近似熵值构建的二维特征向量通过RVM分类识别，并与经EMD分解后的互近似熵值分类识别结果对比可知，本文提出的方法能够对滚动轴承外圈故障点所处方位进行评判，并具有更高的准确率。