烟花搜索导向的多路启发式聚类算法

吴 昊, 王冠凌

(安徽工程大学 电气工程学院, 安徽 芜湖 241000)

聚类是一种重要的数据处理技术，广泛应用于数据挖掘、机器学习等领域[1-2]。在信息量爆炸的当代，数据处理技术更是成为推动互联网技术发展的驱动力，因此聚类技术能够更好的服务于人们的生活[3-4]。启发式聚类算法是一种求解由组合优化模型描述的聚类问题的有效方法[5-6]。组合优化模型描述的聚类问题概化描述如下：

Drineas等[7]已经证明，即使在K=2的情况下，该聚类问题也是NP-难解的，即不存在多项式时间的精确算法能求得该聚类问题的全局最优解。研究者们往往采用能在较短时间内获得可接受解的启发式搜索(heuristic search)方法来求解该类聚类问题，并设计了经典启发式聚类算法，如K-means[8]、K-mediods[9]、PAM[10]及CLARANS[11-12]等。启发式搜索根据给定的初始解，沿着某个方向进行搜索，直到最终目标函数达到收敛，使其能够在合理的时间内获取近似最优解，图1给出的是启发式算法的搜索过程。图中横坐标表示的是算法的可行解，纵坐标表示的是目标函数值。从图中可以看出：当初始解为A时，目标函数将会收敛于B，当初始解为C时，目标函数将会收敛于D。但D的聚类结果要优于B的聚类结果，所以聚类结果很容易受到初始解的影响。

图1 启发式搜索

为了解决经典启发式聚类算法初始解敏感现象，Ding等[13]在文中将K最近邻或K互最近邻一致性作为数据聚类的重要质量度量方法，给出了K-means-CP算法，在一定程度上改善了聚类结果；李洁等[14]提出了NFWFCA算法，通过计算每个数据点在数据集中的权重，使得聚类结果更准确更高效。通过对多次聚类结果的观察，发现接近80%的局部最优解都集中在全局最优解的周围，该现象被称之为“大坑”现象,Gu等[15]为避免聚类结果陷入局部最优解的陷阱，提出了利用空间平滑策略对原始搜索空间进行“填坑”操作。在此基础上，赵东东等[16]提出了多空间的聚类算法，先在平滑搜索空间中求解问题，再用获得的解引导粗糙搜索空间中问题的解根据“大坑”现象，文献[17-18]提出了近似骨架导向的启发式聚类算法，一定程度提升了算法的运行效率。

文献[19-20]给出了一种群体智能烟花算法(FWA)，该算法受自然界中烟花爆炸现象的启发，适合求解优化问题。组合优化模型描述的聚类问题是典型的优化问题，因此，本文利用烟花搜索的局部寻优能力，给出了一种烟花搜索导向的多路启发式聚类算法(Fire Search Guided Multi-way Heuristic Clustering algorithm，FSG_MHC)。该算法先通过P次调用经典启发式聚类算法，产生P个局部最优解；然后以P个局部最优解为搜索起点，在搜索空间中采用烟花搜索进行多路搜索；对于给定的p∈P路搜索，首先以信息熵浓度为基础，设计烟花选择算子确定搜索方向；再经过变异，偏移，映射算子更替局部最优中心点，获得高质量搜索起点；最后重复上述两步直至算法收敛。

1 符号约定与相关定义

有关烟花搜索导向的多路启发式聚类算法(FSG_MHC)的符号约定和相关定义见表1。

表1 符号约定

(1)

其中Φmax表示目标函数最大值，t是常数，用于调整产生的类簇中的样本点个数的大小。

(2)

(3)

定义3沿着信息熵浓度下降方向进行搜索可获得比初始的局部最优解更加理想的聚类结果。

(4)

其中U(-Ap,Ap)为烟花的偏移范围。

(5)

其中g为满足高斯分布的任意随机数。

(6)

其中XLB,k，XUB,k分别表示烟花边界(最小值)、烟花边界最大值。

2 烟花搜索导向的启发式聚类算法

烟花搜索导向的多路启发式聚类算法(FSG_MHC)的基本框架及时间复杂度分析如下。

图2 FSG_MHC程序框图

烟花搜索导向的多路启发式聚类算法共有5部分组成，在算法1主函数中，先产生初始种群集合MP，对集合MP进行启发式搜索，在搜索的过程中通过烟花搜索产生新的局部最优解集合NS，最后对集合NS降序排列，输出全局最优解。算法2和算法3是确定聚类之后簇群的范围和簇群中数据样本点的个数。图2为整体程序框图。

2.1 FSG_MHC算法框架

算法1给出FSG_MHC算法框架。FSG_MHC算法在P个局部最优解集合MP中进行烟花搜索，来发现新的搜索起点NS，再以NS为初始解调用经典启发式聚类算法产生高质量聚类结果。

算法1 FSG_MHC

输入：Dm，K，MP; 输出：C。

1.NS←φ,C←φ；

2.do

(1)S←findfireset(MP,P)；

(2)A←CalfireR(MP,P)；

(3) 任意Mp∈MP,p=1,2,…,P

5.以NS为搜索起点调用经典启发式聚类算法产生聚类结果C；

6.returnC。

从算法1中可以看出，FSG_MHC算法在给定P个局部最优解集合MP的基础上完成以下4个部分：

(1)NS与C的初始化。

(2)对MP集合进行多路烟花搜索操作：首先调用findfireset和calfireR函数确定P个中心点集合的每个中心点搜索空间与范围；再采用信息熵浓度方法选择最有可能成为新的搜索点的中心点，针对该中心点执行烟花搜索；在搜索过程中采用偏移和变异算子在S和A的范围内产生新的替代中心点，如果替代中心点超出了烟花范围，则采用映射原则进行修正；将新的中心点替换已有中心点后产生一个新的中心点集合；如此迭代直到前后两代目标函数最小值之间的误差小于10-3时收敛。

(4)以NS为起点调用经典聚类算法产生数据集Dm的聚类结果C。

算法2给出了findfireset的基本框架，可以看出，findfireset采用定义1给出的公式计算Mp中所对应的烟花个数Sp，获得烟花集合S，确定了每个中心点在搜索空间中的搜索范围。

算法2 findfireset

输入:MP，P； 输出：S。

1. forp=1 toPdo

(1)Sp←0；

(2) 采用定义1给出的公式计算Mp所对应的烟花个数Sp；

2. end;

3. returnS。

算法3给出了CalfireR函数的基本框架，可以看出，CalfireR采用定义2给出的公式计算Mp所对应的烟花半径Ap,获得烟花半径集合A，确定了每个中心点在搜索空间的搜索半径。

算法3 CalfireR

输入:MP，P； 输出:A。

1. forp=1 toPdo

(1)Ap←0；

(2) 采用定义2给出的公式计算Mp所对应的烟花半径Ap；

2. end;

3. returnA。

2.2 时间复杂度分析

FSG_MHC算法的时间消耗主要发生在多路烟花搜索过程，在该过程中调用findfireset和calfireR函数确定MP中每个中心点搜索空间与范围的时间复杂度为O(K*P*(|S|+|A|))，而在S*A搜索空间中进行多路搜索的时间复杂度为O(P*(|S|*|A|))。

根据以上分析，假定主函数循环次数为T，该算法的时间复杂度为O(T*((P*(|S|+|A|))*(K+1)+2+P)+1+Δ)，其中T,P,S,K≪N；O(Δ)为传统启发式聚类算法的运行时间。

3 实验分析

本文在4个数据集中对比了FSG_MHC和4个经典启发式聚类算法CLARANS[11]、K-means[21]、FCM[22]、Kd-tree[23]的聚类质量。表2给出了6个数据集的基本情况，包含1个随机数据集和5个从UCI网站上下载的真实数据集。为了适应算法比较，本文选取了5个真实数据集的数值型数据。

表2 数据集信息

实验在Windows 7系统下，采用MATALB2016语言编程环境，Intel Corei5 2.6 GHz CPU时钟频率，4 GB内存。

FSG_MHC通过搜索空间重构及搜索空间中信息交互方法达到提高启发式聚类算法获得高质量聚类结果的概率，即获得评价函数取值更小的聚类结果。因此，本文在实验中采用目标函数值作为聚类算法的评价标准，即目标函数值越小，聚类质量越高。

图3给出了5个对比算法在6个不同数据集上的聚类质量对比结果。从图中可以看出在6个数据集上FSG_MHC算法的目标函数值要小于其对比算法的目标函数值，这说明FSC_MHC算法的聚类质量要明显高于对比算法的聚类质量。由于FSG_MHC在P个局部最优解中利用烟花搜索算法的局部寻优能力发现质量更高的搜索起点，再以新的搜索起点调用经典启发式聚类算法获得聚类结果，因此聚类质量更高。从图3中还可以看出在数据集StatlogHeart上，5种对比算法的聚类效果不是特别理想，这是因为StatlogHeart是高维数据集，影响了5种对比算法的聚类质量，说明5种对比算法在处理高维数据方面还有欠缺。

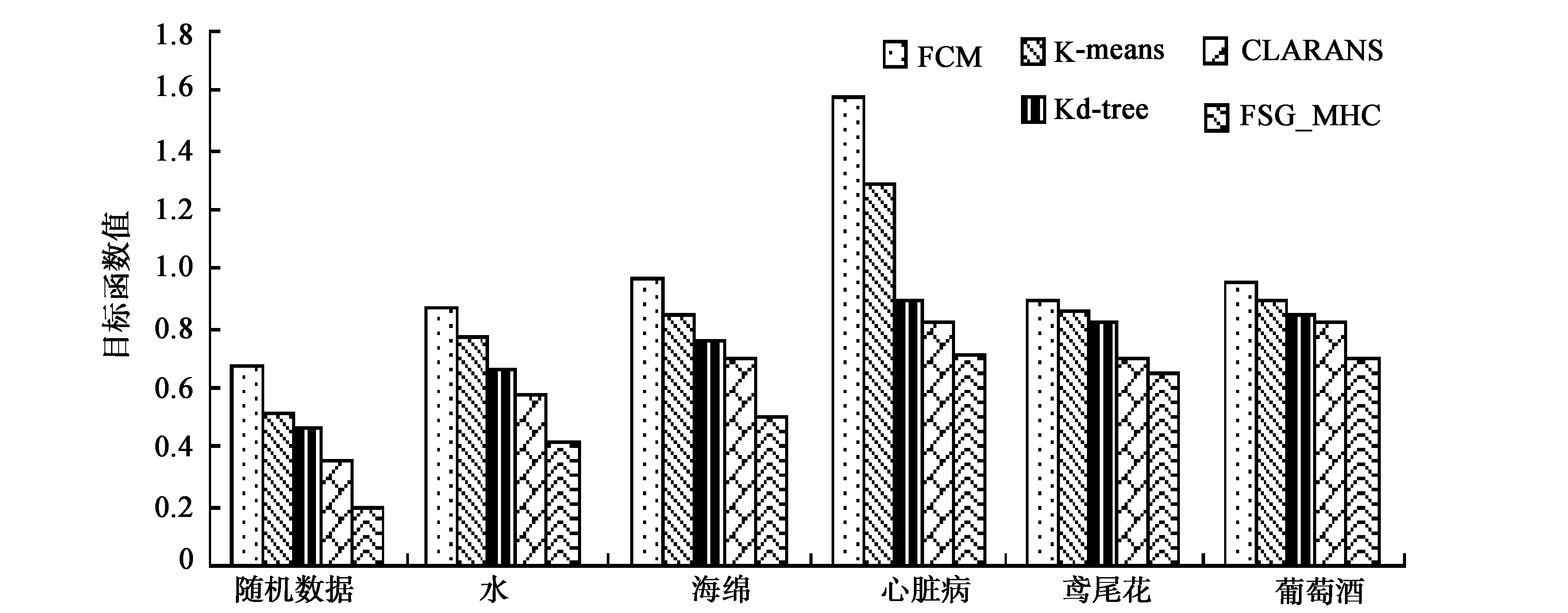
图3 聚类结果对比

表3给出了5种对比算法在6个不同数据集上的运行时间，从表中可以看出K-means算法是运行速度最快。本文提出的FSG_MHC算法在P个局部最优解中进行搜索，其时间复杂度仅与P、S、K等因素相关，因此其运行速度较快，仅次于K-means算法，这说明算法FSG_MHC在可行算法时间内可以获得更高质量的聚类结果。

表3 运行时间对比 s

4 结 论

将烟花搜索和启发式聚类算法相结合，解决了初始解敏感的问题，提高了聚类质量。给出了烟花搜索导向的多路启发式聚类(FSG_MHC)的算法框架，并通过实验对比了FSG_MHC和FCM，K-means，Kd-tree以及CLARANS的聚类结果。实验结果证明烟花搜索对启发式聚类是十分有效的，而且无论是从运行时间还是聚类结果来说本文算法都优于对比算法。下一步的研究将重点致力于将FSG_MHC算法应用到实际工程应用当中，如无线传感网、室内定位等领域，更好的完善算法。