在直观操作中发展学生的数学抽象素养
——以“从拼长方形到二次三项式的因式分解”为例
丁银杰
(江苏省苏州市草桥中学校 215031)
因式分解是初中数学的重要内容之一,有着广泛的应用.《苏科版义务教育教科书·数学》将因式分解安排在七年级下册“整式乘法与因式分解”一章.教材共用4课时介绍因式分解概念和两种因式分解基本方法(提公因式法、运用公式法),此外在“数学活动:拼图 公式”栏目适度拓展了因式分解,但未提及十字相乘法.
对于《义务教育数学课程课标(2011年版)》删去十字相乘法,很多学者和一线教师都颇有微辞.实际教学中,教师会根据学情用1到2个课时补充十字相乘法,以满足后续学习的需要.
相对于提公因式法和运用公式法的“机械算”,十字相乘法重在“灵活凑”,需要一定的开放、直觉思维作为支撑.常规教学一般从多项式乘法出发.从纯“数”的角度讲解十字相乘法,重点讲解形如x2+bx+c的二次三项式的因式分解,学生难以理解“十字交叉”的意义.
笔者以某次公开教学研讨课为契机,对十字相乘法进行了大胆的创新教学实践,借助于直观操作——“拼”长方形,数形结合,突破难点,帮助学生理解“凑”因式的数学原理,进而抽象出“十字相乘法”,从中发展学生的直观想象和数学抽象素养.
1 类比——寻求思路
G·波利亚曾说:“类比是提出新命题和获得发现取之不竭的源泉”,类比法是由两个或两类对象在某些方面的相同或相似,作出它们在其他方面也可能相同或相似的推理方法,属于合情推理.类比完全平方式可用正方形表征,获得一般的二次三项式可用长方形表征的猜想,这为一般的二次三项式的因式分解提供了解决问题的思路.
在教学的第一环节设计了如下的问题情境:
(1)如图1,A卡片是边长为x的正方形,B卡片是边长为y的正方形,C卡片是长为x、宽为y的长方形.

图1
请用A、B、C三种卡片分别拼一个面积为x2+2xy+y2、4x2+4xy+y2的正方形,并根据图形,写出多项式x2+2xy+y2、4x2+4xy+y2因式分解的结果;
(2)请尝试用A、B、C三种卡片拼一个面积为x2+3xy+2y2的正方形或长方形,并根据图形,写出二次三项式x2+3xy+2y2因式分解的结果.
本节课学生学习的起点是用完全平方公式把完全平方式分解因式,目标是学会用十字相乘法把二次三项式分解因式,这在认识上属于由特殊到一般.让学生明白“学什么”和“怎样学”是本环节的主要任务.
首先,通过拼正方形,直观表征完全平方式,赋予完全平方式“形”的特征,再根据部分与整体的关系,把完全平方式分解因式.
其次,给出x2+3xy+2y2,让学生“碰壁”(不能使用完全平方公式分解),激发求知和探究欲望,明确本节课的学习主题——二次三项式的因式分解.在此基础上,引导学生类比,赋予二次三项式x2+3xy+2y2几何意义,将“数”转化成“形”,通过“形”的化零为整,拼出大长方形,再借助于“形”的直观回到“数”,把二次三项式x2+3xy+2y2分解因式,获得初步体验,为后续探究做好心理和认知准备.
2 操作——抽象方法
数学抽象是指抽取出同类数学对象的共同的、本质的属性或特征,舍弃其他非本质的属性和特征的思维过程.正如华罗庚所说的那样,“数缺形时少直观,形少数时难入微.数形结合百般好,隔离分家万事休.”图形的直观为方法的抽象提供了直觉支撑.
在教学的第二环节设计了如下操作与探究活动:
(1)操作与思考:
借助拼长方形,把下列二次三项式分解因式:
①x2+7xy+6y2;②x2+5xy+6y2;③3x2+7xy+2y2.
(2)归纳与抽象:
若ax2+bxy+cy2=(a1x+c1y)(a2x+c2y)(a、b、c、a1、a2、c1、c2均为正整数),则a与a1、a2,c与c1、c2,b与a1、a2、c1、c2有怎样的数量关系?
本环节的核心任务是借助图形的直观,初步抽象出十字相乘法的一般方法,关键是借助A、B卡片分别拼成的两个小长方形(或正方形)帮助学生理解“拆两头”,借助C卡片拼成的两个小长方形理解“交叉相乘凑中间”的意义,体会“拆的自由”与“凑的约束”之间的辩证关系.
对于同一个二次三项式,由于拼长方形的方式不同,得到的图形也不同(图2是学生根据x2+5xy+6y2拼出的几种不同图形).尽管这不影响因式分解结果,但不利于方法抽象,教师在学生拼图过程中要适时引导,让学生认识有序拼图的重要性(如将A、B、C三种卡片分别拼在长方形的左上角、右下角、左下角和右上角).

图2
如图3-1,从“形”上看,面积为x2+7xy+6y2的长方形长、宽分别为x+6y、x+y,可分为4个小长方形(或正方形):分别是边长为x的正方形(面积为x2),长、宽分别为6y、y的长方形(面积为6y2),与2个长、宽分别为x、y与6y、x的长方形(面积和为7xy).从“数”上看,x2+7xy+6y2与其两个因式x+6y、x+y之间的数量关系可用图3-2表示.整个分解因式的思维过程可概括为“拆两头(x2=x·x,6y2=6y·y),交叉相乘相加凑中间(x·y+6y·x=7xy)”.
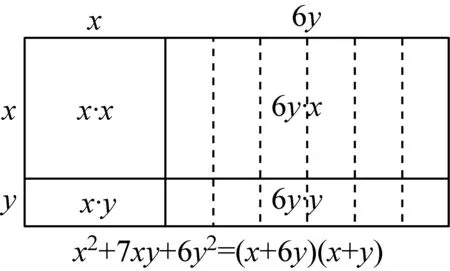
图3-1

图3-2
对于x2+5xy+6y2,拼成的长方形如图4-1,x2+5xy+6y2与其两个因式x+3y、x+2y之间的数量关系可用图4-2表示.

图4-1

图4-2
对于3x2+7xy+2y2,拼成的长方形如图5-1,3x2+7xy+2y2与其两个因式3x+y、x+2y之间的数量关系可用图5-2表示.

图5-1

图5-2
对于ax2+bxy+cy2(a、b、c为正整数),不难结合图6-1,得出若ax2+bxy+cy2=(a1x+c1y)(a2x+c2y),则a=a1a2,c=c1c2,b=a1c2+a2c1,各系数之间的关系可用图6-2表示.若只保留系数,图6-2可简化为图6-3.这样便抽象出具有“形”的背景的十字交叉相乘的“数”的结构,完成二次三项式因式分解一般方法——十字相乘法的初步构建.
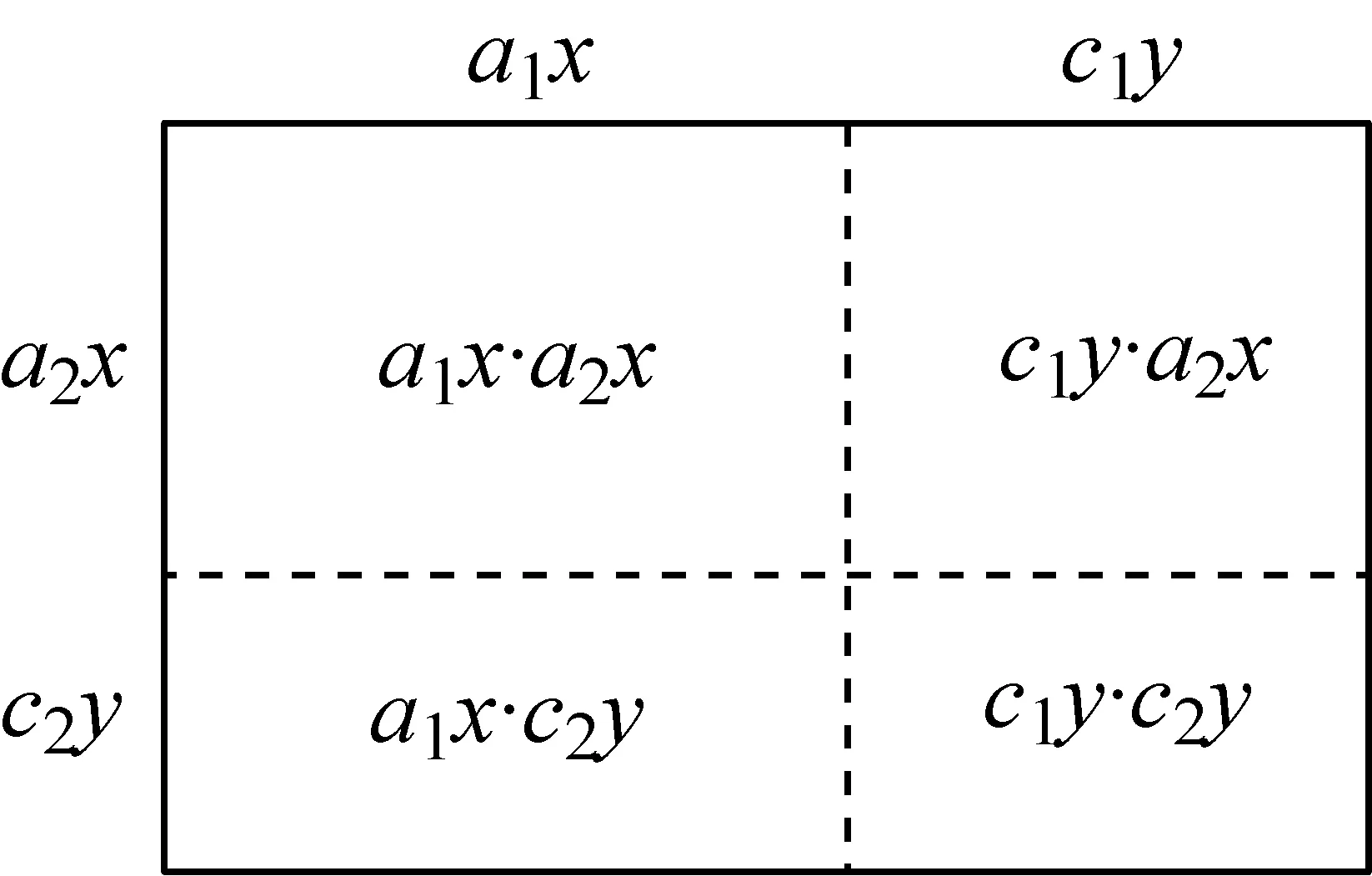
图6-1

图6-2

图6-3
3 变式——提升能力
顾泠沅在分析、反思中国数学课堂时,认为变式教学是一种中国盛行的数学教学方法,满足了数学教学的两个目标:(1)通过使用概念性变式, 从多角度理解数学对象(概念和原理);(2)采用过程性变式开展有层次的数学活动.
为了完备对十字相乘法的构建,体现十字相乘法的应用价值,在教学的第三环节设计了如下变式探究:
(1)一般地,若ax2+bxy+cy2=(a1x+c1y)·(a2x+c2y)(a、b、c为常数),则a与a1、a2,c与c1、c2,b与a1、a2、c1、c2有怎样的数量关系? 请说明理由.
(2)根据(1)中的各系数之间的数量关系,把二次三项式x2+2xy-3y2分解因式,请用A、B、C三种卡片拼一个面积为x2+2xy-3y2的长方形(允许图形有部分重叠).
(3)用十字相乘法,把下列二次三项式分解因式:
①4x2+12x+9;②x2-0.5x+0.06;
③(s-t)2-2(s-t)-3.
在前面操作、抽象的基础上,学生不难回归“数”,利用多项式乘法,经历再次抽象,将直观拼图获得的抽象方法拓展到一般情形,完备对十字相乘法的认识与构建.
正是有了动手“拼”的经验,头脑中有了“形”的意象,眼中的“数”才具有灵动的意义.此时 “拆”和“凑”不再依赖实物操作,在思维的指引下,便可得到图7-1,即x2+2xy-3y2因式分解的结果为(x+3y)(x-y).

图7-1
拼面积为x2+2xy-3y2的长方形意不在验证,而在进一步拓展学生的思维,以数御形,发展学生的直观素养.学生先前获得的经验是:当二次三项式各项系数皆为“+”号时,拼图过程是一个不断向外“扩张”的过程,当系数出现了“-”号时,图形可以适度重叠,向内“缩小”.如图7-2,在x2+2xy-3y2=(x+3y)(x-y)的启发下,先用1张A卡片、3张C卡片拼出一个大长方形,再用1张C卡片、3张B卡片拼出一个小长方形,然后用小长方形覆盖大长方形,这样大长方形未被覆盖部分的面积就是x2+2xy-3y2.
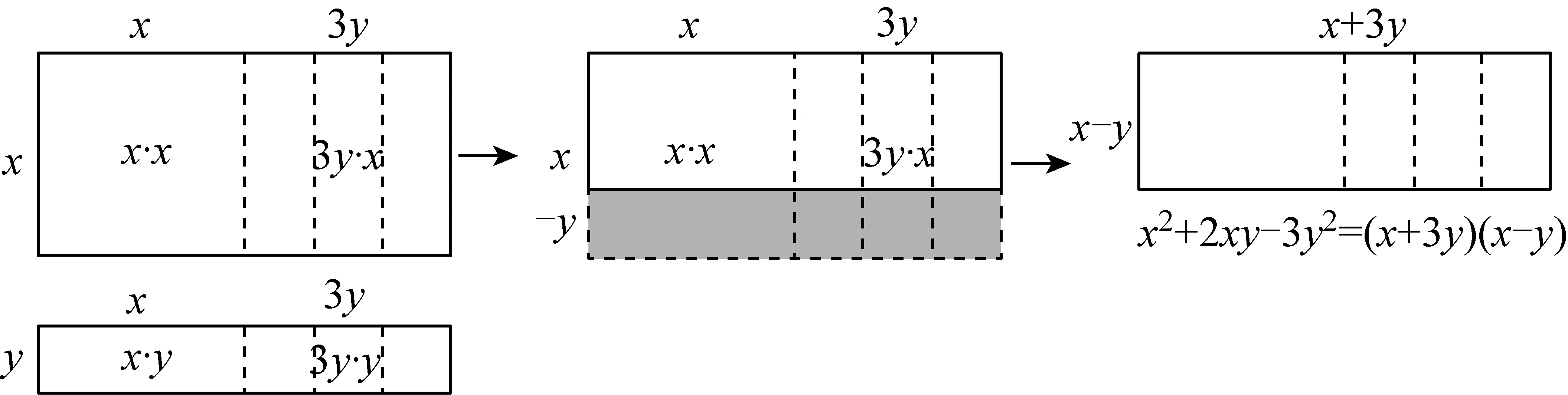
图7-2
此外,学生通过变式训练可以感受十字相乘法的普适性.二次三项式各项的系数可以是整数也可以是分数或小数;多项式只需是关于某一“主元”的二次三项式,“主元”可以是单项式或多项式.
如,多项式4x2+12x+9可以看作是4x2+12xy+9y2中字母y=1的特殊情形;若令s-t=x,则(s-t)2-2(s-t)-3可化为x2-2x-3.
变式训练还力求让学生感受十字相乘法的包容性.通过变式训练让学生明白运用公式法(平方差公式和完全平方公式)是十字相乘法的特例.
如,4x2+12xy+9y2=(2x+3y)(2x+3y),4x2-9可看作4x2+0x-9.
4 反思
(1)情境与目标
教学情境是为落实教学目标而设计的引导性问题或操作活动.好的情境符合学情、遵循认知和教学规律,有利于教学目标的实现.在本节课的教学中,设计了拼长方形的问题情境,较之直接从因式分解与整式乘法的关系,从纯“数”的角度去探究,拼长方形的问题情境直观性和操作性强,能调动学生多种感官参与认知,整个过程摸得着、看得见、说得清、想得通,大大降低了探究的难度,有利于教学目标的达成.这一设计很好地体现了数学实验的“手脑协同,启思明理”的教学主张.
(2)直观与抽象
直观想象和数学抽象都是应着力发展的数学学科核心素养,两者有着密不可分的天然联系,图形的直观与直觉思维为数学抽象提供素材,数学抽象是直观想象的高度概括.根据儿童思维发展理论,小学生的思维以具体形象思维为主要形式,到了初中阶段,逐步过渡到以抽象逻辑思维为主要形式,但抽象思维水平仍然较低,对数学知识的理解离不开直观形象的支撑.从图形的直观抽象出具有“形”的特征的“数”的结构,不仅符合学生的认知心理,而且有力促进了学生数学抽象素养的提升.正是因为“数”的结构固着了“形”的特征(上下两行分别对应长方形的长和宽),十字相乘法教学中的典型错误(根据图6-2,将因式分解的结果写成(a1x+c2y)(a2x+c1y))显著减少了.
本节课的教学绝不仅仅是十字相乘法技能的传授,拼图情境贴近学生心理,降低了思维难度,操作探究提供足够的直观支撑,拉长了思维过程,有利于学生在直觉思维的参与下,不断抽象,完成十字相乘法的自主构建.

