基于飞行科目统计分析的严重谱编制方法

张佳佳，蒋祖国，冯建民

(1.中国飞机强度研究所 全尺寸飞机结构静力/疲劳航空科技重点实验室，西安 710065) (2.中国飞行试验研究院 强度部, 西安 710089)

0 引 言

在现有试验技术水平下，国内飞机的全尺寸疲劳试验一般需要花费较长的时间(一般为4倍寿命，5～8年)，已经成为影响型号研制周期的关键因素之一[1]。过长的疲劳试验周期，成为制约我国飞机研发的瓶颈，影响着整个飞机技术和产业的发展[2-4]。通过对飞机结构寿命分散性的研究，提出分散系数与载荷谱严重程度有关的观点[5]，即采用严重谱可以减小疲劳寿命分散系数[6]，能够大幅缩短试验时间至2倍寿命，具有重大的工程意义。

2008年，国军标GJB 67.6A-2008对编制耐久性严重载荷谱提出了明确要求[7]，但由于国内在严重谱方面研究较少，目前绝大多数型号编制和使用的飞机载荷谱仍为平均谱，即代表飞机平均使用情况的疲劳载荷谱[8]。平均谱只能够代表50%的损伤覆盖率和使用寿命期内机队50%飞机的预计使用情况，其代表性和真实性远逊色于严重谱。

严重谱的概念在美国国防部发布的新版联合使用规范指南《飞机结构》(JSSG-2006)[9]中首次提出“编制耐久性设计使用载荷谱，以反映飞机在设计使用分布内的严重使用情况，从而使机队90%的飞机满足预期使用寿命”。从损伤角度来说，耐久性载荷谱应反映90%载荷损伤覆盖概率下的使用情况；从寿命角度来说，严重谱代表了使用寿命期内机队至少90%飞机预计的使用情况[10]。

飞机结构设计思想对损伤容限设计和耐久性设计提出了新要求[11]。解决编谱问题对新一代飞机的研制和定寿，贯彻执行新的国军标都迫在眉睫，是研究严重谱分散系数，严重谱下结构使用寿命[12]和严重谱工程应用等后续研究的基础。

国内外针对不同类型的载荷谱有不同的编制方法，早期欧洲使用的是TWIST方法[13]编制飞续飞随机谱，为加速全尺寸疲劳试验历程，提出了雨流计数和等损伤折算的简化编谱方法[14]。FAA通过对通用类航空飞机标准过载数据的统计分析，编制出了单机和各个作业机组的突风谱和机动谱[15]。国内采用的基本编谱方法是任务分析法[8]，在其基础上做出了代表中值损伤、结合飞行大纲、全信息代表飞行起落法等探索[16-19]。

为了编制严重谱，国内学者讨论了载荷谱损伤分散性的描述方法[20]，阐明了寿命分散性的含义，提出了严重谱损伤选取准则，并建立了基于载荷因子-累计超越数曲线族[21]的严重谱的包线选取方法[22]，但没有得到基于任务分析法的具体严重谱编制方法与结果，对于严重谱的编制流程和参数选择，尚无明确方法与步骤。

本文以我国某教练机标准化后的起落数据为基础，提出基于飞行科目统计分析的严重谱编制方法，建立完整的编谱流程，计算出加权平均谱，一倍、两倍标准差谱，90%/95%严重谱的使用情况，得到飞行科目严重谱和总严重谱；通过K-S检验方法验证载荷损伤分布的合理性，根据当量损伤计算结果给出严重谱代表起落的选取方法。

1 数据选择与编谱方法

1.1 原始数据与任务剖面的选择

原始数据为某教练机实测重心过载谱经过标准化处理后的起落数据，含8种任务剖面的246个飞行起落数。参考文献[8]给出的飞机编谱用典型任务剖面的飞行科目，包含飞行起落数、一次飞行时间、使用时间比例、起落代号等参数，具体参数如表1所示。

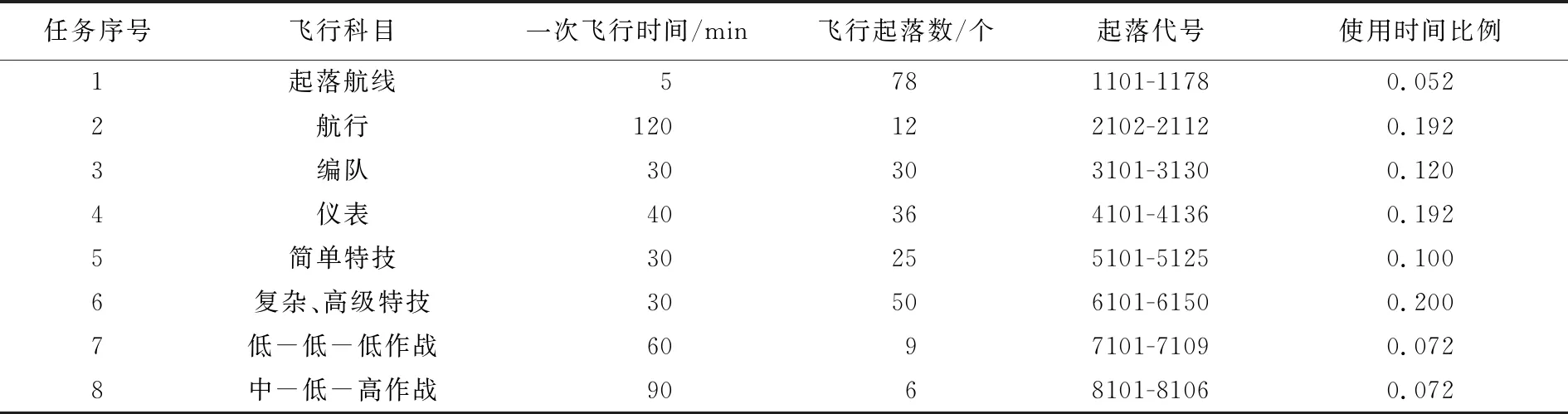
表1 典型飞行科目参数表

1.2 飞行科目统计分析法的基本思想

编制严重载荷谱的飞行科目统计分析法结合了国内编制载荷谱的任务分析法[8]与FAA处理载荷数据的统计思想[15]，以机队飞机飞行科目为编谱单元，由此编制机队飞机每个飞行科目的严重谱和总严重谱。

2 严重载荷谱编制

本节以编制重心法向过载为主参数的参数严重谱为例来阐述飞行科目严重谱编制方法的具体实施步骤，重点讨论其计数、拟合、统计等步骤。

2.1 计数统计处理

输入机队飞机飞行科目压缩的重心过载及飞参历程后，按双参数循环计数法分别计数该起落重心法向过载nz的所有峰值和谷值，对于每个起落，采用了首尾相连的办法使其成为全循环或半循环谱。计数的峰值用加权平均的方法归并到相应的载荷级中，对于国内教练机起落数据，确定了以0.5为间隔的10个载荷级，即峰值范围1.5～6.5，谷值范围-0.5～4.5。统计每个飞行科目每次飞行各级nz及相应辅助参数实有出现频数。

实有频数计数完成后，分别计算同一飞行科目每次飞行的峰值载荷和谷值载荷的累积频数，并标准化1 000飞行小时。假设某型飞机有m个飞行科目，每个科目含n次起落飞行，则一共要计算2mn个重心载荷nz累积频数谱。

2.2 确定载荷情况

所谓确定载荷情况，就是如何组合飞行科目剖面的性能参数、结构载荷环境的响应参数和其他相关参数，以形成不同的载荷状态，作为载荷计算和应力分析的输入。一般用飞行参数的统计分布组合方法来确定载荷情况[8]。

2.3 参数拟合

参数拟合包括曲线拟合和高载外推拟合。参数拟合能更好把握机群过载与累积频数的关系，由此形成飞行科目拟合函数曲线，便于编谱的后续处理。

由于本文使用对数多项式进行拟合，故在进行曲线拟合时，对负的载荷谷值，取nz=|nz|；对0过载，取nz=0.01。

2.3.1 曲线拟合

在一般情况下，可用如下对数多项式方程进行曲线拟合

lgy=a0+a1x+a2x2+a3x3+a4lg(x)

(1)

当编制以重心过载nz为主参数的严重载荷谱时，可把式(1)变成如下形式

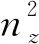
(2)

式中：F(nz)为各级重心载荷nz的累积频数；nz为重心法向载荷；a0，a1，a2，a3，a4为曲线拟合得到的系数。

当取a0，a1，a2，a3，a4中的两项或三项为0时，可获得较好的拟合性[15]。通过最小二乘法进行拟合，拟合结果为曲线与原始数据偏离最小且变化趋势相同。

2.3.2 高载外推

尽管通过实测起落数所获得的编谱数据考虑了各种使用情况和所有飞行科目，大载荷出现的概率更大些，但毕竟飞机是在和平环境下的训练飞行或运营飞行，飞机在极端恶劣环境中飞行的机率很小，很难出现一个寿命期内等于或大于最大载荷的情况，因此编制严重谱需要更多地考虑飞机最严重的使用分布情况。考虑到编谱数据的局限性，编谱过程中需要进行高载外推。

用对数线性外推方法对拟合曲线进行外推，令式(2)中的a2，a3和a4均为0，由此可得对数线性外推的一般方程

lg[F(nz)]=a0+a1nz

(3)

用式(3)进行外推时，每次飞行拟合曲线最高两级的载荷和累积频数作为原始数据进行线性拟合，得到每次飞行外推的对数线性方程。

2.4 绘制飞行科目载荷拟合函数曲线

根据建立的曲线拟合方程和高载外推方程，绘制含外推部分的飞行科目载荷拟合函数曲线，如图1所示：图中为高级复杂科目的2×50条曲线。

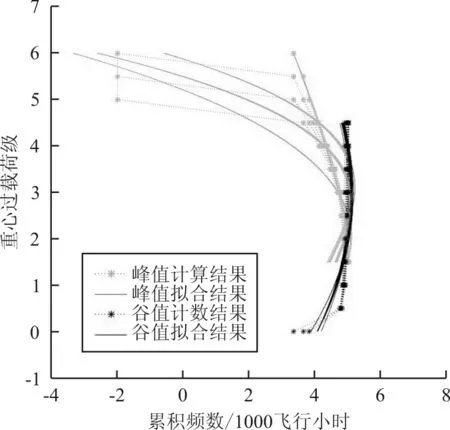
图1 复杂高级特技科目曲线拟合结果

2.5 计算加权平均值和标准差

根据某飞行科目的n次飞行起落的n条重心过载nz的拟合曲线，可得到各级过载nz的累积频数y(即F(nz))，由此可按式(4)和式(5)计算加权平均值yw和加权标准差sw。

(4)

(5)

式中：ti为第i次飞行起落该飞行科目的飞行小时数；T为该型号飞机该飞行科目的总飞行小时数；yi为第i次飞行起落该飞行科目各级载荷(重心过载)累积频数。

该型号中的每架飞机在执行同一飞行科目任务时，其飞行结果具有较大的分散性，计算加权平均值和加权标准差是为了抵消这种分散性。由于该型飞机有m个飞行科目，需要计算m次加权平均值和加权标准差，本文中m=8。

2.6 计算置信度谱

考虑到国军标GJB67.6A-2008规定的耐久性严重载荷谱是按90%存活概率给出，本文的最终严重载荷谱按90%概率值、95%置信度值的置信度谱确定，该置信度谱简称90%/95%谱，90%/95%谱的数学表达式如下

Y90/95=μ+δ

(6)

式中：Y90/95为存活概率90%、置信度95%的载荷累积频数；μ为置信度为95%时的总体平均估计值；δ为相应于存活概率为90%时的总体分散度。

在一般情况下，总体平均值μ的90%置信度值可由式(7)求得

(7)

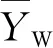
90%存活概率的分散度δ的相应计算式如下：

δ=1.282σ

(8)

(9)

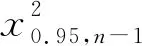
根据式(4)～式(9)的计算结果，编制出该机队的加权平均谱和各种严重载荷谱，包括(μ+1σ)谱、(μ+2σ)谱和90%/95%谱。

2.7 编制飞行科目加权平均谱和各种严重谱

根据2.5 节和2.6节的计算结果，编制每个飞行科目的加权平均谱和各种严重载荷谱，复杂高级特技科目严重谱编制结果如图2所示。

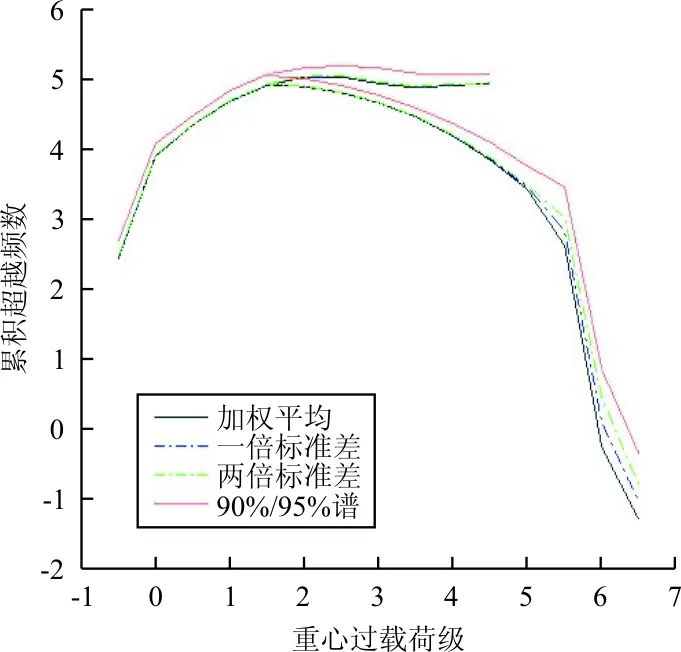
图2 复杂高级特技科目严重谱编制结果

2.8 编制总谱

由飞行科目剖面资料可获得每个飞行科目的使用百分比μi，把所有的μi用矩阵形式表示为

M=[μ1,…,μi,…,μl]

(10)

式中：M为飞行科目的使用比例矩阵；μi为第i个飞行科目的使用百分比，由该科目一次飞行时间与飞行总时间的比值计算；l为飞行科目数。

飞行科目的使用比例矩阵M乘以飞行科目谱矩阵F即为总谱G，即

G=M·F

(11)

或

(12)

式中：G为总的各级载荷累积频数矩阵；gj为第j级载荷累积频数，编谱结果如图3所示。

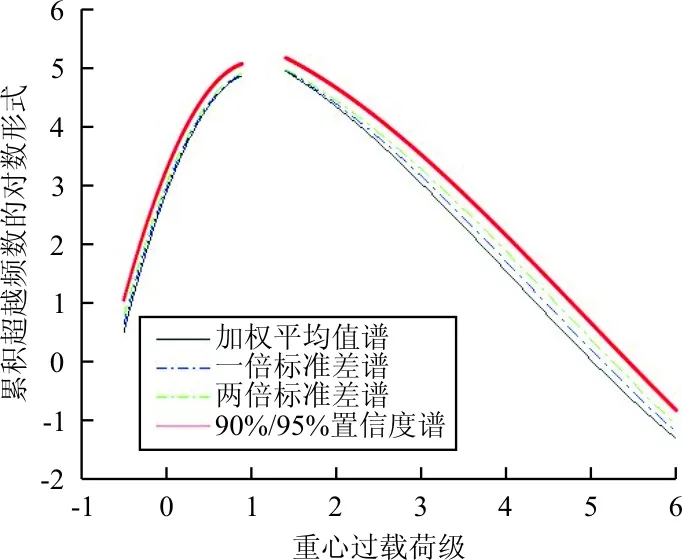
图3 飞行科目统计方法总严重谱编制结果

3 严重谱代表起落的选取方法

本文根据当量损伤值的统计分析结果选取严重谱代表起落。

3.1 当量损伤的计算方法

针对某教练机飞机下翼根部关键部位，采用线性累积损伤理论[23]和奥丁变换法进行当量损伤的计算。

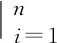
(13)

式中：f(ΔGi,Ri)为第i次循环对应的当量损伤。

3.1.1 当量损伤的理论基础

指定应力比下的S-N曲线用幂函数表示，即

SmN=C

(14)

根据线性累积损伤理论，单个循环损伤为

(15)

式中：Ci，Si为第i次应力循环下的S-N曲线参数；Ni为给定循环下的寿命。

累积各次循环损伤得到全部循环损伤为

(16)

将各次载荷循环当量折算为等损伤的脉动循环S0i，得到

(17)

式中：C,m为脉动循环下S-N曲线参数。

在工程上可以略去少量其他载荷状态循环与亚音速对称状态的差别[3]，故在飞机对称飞行占主导地位的情况下，可以假定关键部位的应力与过载成线性关系。即有

Si=σlg·Gi

(18)

式中：σlg为单位过载对应的关键部位名义应力。

将式(18)带入式(17)，即

(19)

引入与dn呈线性关系的当量损伤为

(20)

式中：ΔG0i为第i次过载循环对应的脉动过载变程。

3.1.2 确定当量损伤的关键问题

由式(20)，确定当量损伤，关键问题是确定S-N曲线参数m的值和每个载荷循环的当量脉动过载变程ΔG0i。

m值应综合多个材料、结构形式不同的关键部位进行选取。文献[24]给出了综合考虑飞机结构多个关键部位不同材料及细节形式，在一般飞机载荷历程下的m值在4左右的结论。本文中取m=4。

计算当量损伤可采用奥丁变换方法，将任一级过载循环(ΔGi,Ri)等损伤折算为当量脉动循环ΔG0i。

(21)

3.2 当量损伤的分布检验

以复杂高级特技飞行科目为例，对于每个起落，雨流计数时抽取其中的全循环与半循环，由式(21)算每个起落的当量损伤。验证其损伤分布合理后，即可按统计方法进行代表起落的选取。

3.2.1 分布形式

对于军机机群载荷损伤分布，一般认为其符合对数正态分布：

(22)

式中：μ为对数正态期望；σ为对数正态分布标准差。

将分布函数线性化后得到标准正态分布的线性检验方程：

lgx=μ+upσ

(23)

式中：up为标准正态分布p分位点。

3.2.2 K-S检验方法

哥尔莫柯洛夫-斯米尔诺夫(K-S)检验方法需要检验的假设是

H0∶f(X)=F0(x)

(24)

式中：F0(x)为完全确定的(不包含任何未知参数)连续型分布函数。

为了寻找检验统计量，将子样(x1,x2,…,xn)的各分量按大小重新排成x(1)≤x(2)≤…≤x(n)。子样的经验分布函数Fn(x)为

(25)

K-S检验统计量为

(26)

只要给定了显著度α就可按条件

P(Dn>Dn,α)=α

(27)

从K-S检验临界值(Dn,α)表中查出Dn,α值。

现计算Dn的取值，由于Fn(x)为单调非降阶梯函数，F0(x)为单调非减函数，所以|Fn(x)-F0(x)|的上确界可在n个点X(i)(i=1,2,…,n)处找。用δi表示X(i)处的经验分布函数与假设的分布函数之间偏差中大的一个，即

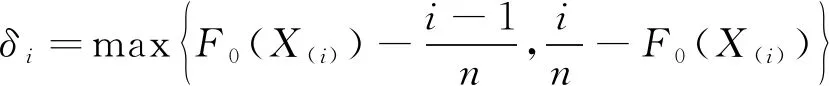
(28)

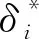
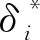
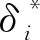
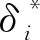
3.2.3 载荷损伤值的分布检验

针对复杂高级特技这一科目50个起落的损伤计算结果，用K-S方法进行检验，假设损伤值满足对数正态分布。

当量损伤的计算结果为(按升序排列，取对数)：

1.859 3 2.043 0 2.094 5 2.138 8 2.159 5

2.210 6 2.319 4 2.342 2 2.354 0 2.412 5

2.439 4 2.467 1 2.502 8 2.503 8 2.576 4

2.601 6 2.613 8 2.637 4 2.655 9 2.662 6

2.666 9 2.671 4 2.692 4 2.707 1 2.718 6

2.801 7 2.902 3 2.943 0 2.946 5 2.948 6

2.973 3 2.976 0 3.084 1 3.092 0 3.132 4

3.154 2 3.185 9 3.246 0 3.265 8 3.389 9

3.620 0 3.679 8 3.725 2 3.757 6 3.770 5

3.786 5 3.844 5 4.259 6 4.944 7 6.212 2

均值为2.973 9，标准差为0.771 2。

假设对数损伤值X满足正态分布N(2.973 9，0.771 22)即原假设为

H0(X)∶X·N(2.973 9，0.771 22)

(31)

要求X的分位数Xα可转化为求N(0,1)的分位数，此时有

xα=σzα+μ

(32)

由式(32)计算得到每个样本对应分位数Xα，查标准正态分布表得对应的分布函数值F0(Xi)。

当显著度取0.05时，查表得K-S检验临界值D50，0.05=0.189>0.14

当显著度取0.10时，查表得K-S检验临界值D50，0.10=0.169>0.14

故接受假设H0，即当量对数损伤值满足标准正态分布，因此损伤值满足对数正态分布。

3.3 根据损伤统计结果选取严重谱代表起落

经检验损伤值合理[26]，故可将损伤结果按照第2节中的思想进行统计分析处理，得到与加权平均谱、一倍标准差严重谱、两倍标准差严重谱，90%/95%谱相对应的损伤值，再根据与其最接近的损伤值对应的起落作为严重谱的代表起落，并记录对应的起落编号。

下表是根据当量损伤值统计分析选取复杂高级特技这一飞行科目的代表起落的结果。

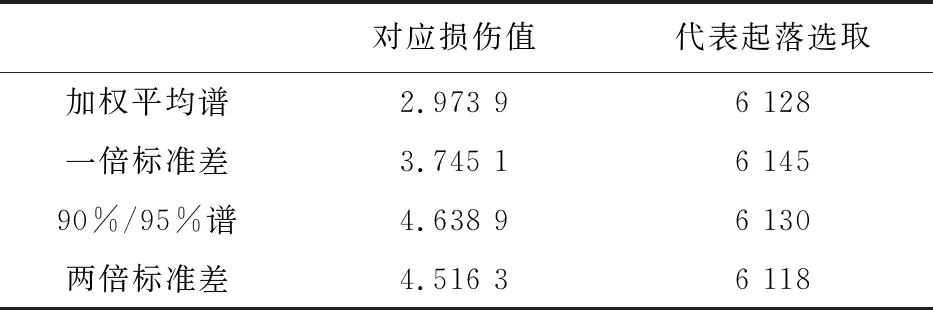
表2 严重谱代表起落选取

按当量损伤统计分析方法选取的代表起落真实有效，载荷谱损伤较大时，试验时间相应缩短。此方法实用性强，可以应用到按不同严重程度进行5×5试验谱或飞—续—飞谱等后续编制工作。

4 结 论

(1) 本文基于飞行科目统计分析的编谱方法，针对我国某教练机给出了加权平均值谱，1倍标准差谱，2倍标准差谱，以及90%存活概率和99%置信度的严重载荷谱。

(2) 通过观察载累积频数分布曲线，起落越多，载荷分散性越大。由于飞行科目差异，起落情况复杂，载荷峰值载荷分散性较大，谷值载荷分散性较小。

(4) 采用严重谱可以降低疲劳分散系数以缩短试验时间，在我国各机型的全机疲劳试验中有广阔的应用前景。